Файл: Ответы к экзамену комбинаторный признак умножения. Количество битовых строк длины.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 162

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ВОПРОСЫ и ответы К ЭКЗАМЕНУ Комбинаторный признак умножения. Количество битовых строк длины k. Пусть задана последовательность событий E1, E2, E3, …, Em таких, что событие Е1осуществляется n1способами, и если события E1, E2, E3,...,Ек-1осуществились, то событие Ек может осуществиться nкспособами. Тогда существует n1х n2х n3х … х nтспособов осуществления всей последовательности событий.. Битовая строка – это строка, состоящая из элементов множества{0, 1}, т.е. каждый из элементов имеет значение 0 или 1. Сколько существует битовых строк длины 5? Сколько существует битовых строк длины k?Поскольку каждый символ строки может иметь значение 1 или 0, тосуществует два варианта выбора для каждой позиции. Следовательно, существует 2 x 2 x 2 x 2 x 2 = 25 битовых строк длины 5. По аналогичным соображениям, имеется 2k битовых строк длины k. Количество всех подмножеств k - элементного множества. Число всех подмножеств из элементов равно N(M(A))=2^n Комбинаторный признак сложения.  (Комбинаторный принцип сложения) Пусть S1, S 2, S3,... ,Sm – попарно непересекающиеся множества (т.е. SiSj = для всех i  j), и пусть для каждого i, множество Si содержит niэлементов. Количество вариантов вы­бора из S1 или S2или S3 или ... или Smравно n1 + n2 + n3+ … + nm. На языке теории множеств утверждение теоремы имеет вид |S1 S2 S3 ... Sm|= |S1| + |S2| + |S3| + ... + |Sm|, где |S| обозначает количество элементов множества S. Перестановки, размещения, сочетания без повторения. Перестановками -называются наборы состоящие из одного и того элементов,следования элементов. Pn=n!Размещение –называются упорядоченные наборы из элементов выбранных из n элементов, которые отличаются друг от друга, как порядком следования, так и составом элементов. mA =n!/(n-m)!nСочетание- называютсяэлементов выбранных из n элементов, которые отличаются другот друга составом элементов. mС =n!/m!(n-m)!n Бином Ньютона. Треугольник Паскаля. Свойства биномиальных коэффициентов. Формула бинома Ньютонадля натуральныхnимеет вид  , где   -биномиальные коэффициенты, представляющие из себя сочетания изnпоk,k=0,1,2,…,n, а "!" – это знак факториала).К примеру, известная формула сокращенного умножения "квадрат суммы" вида   есть частный случай бинома Ньютона приn=2.Выражение, которое находится в правой части формулы бинома Ньютона, называютразложениемвыражения(a+b)n, а выражение   называют(k+1)-ым членом разложения,k=0,1,2,…,n.Биномиальные коэффициенты для различныхnудобно представлять в виде таблицы, которая называется арифметическийтреугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид: Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральныхn: Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.Для коэффициентов бинома Ньютона справедливы следующие свойства: коэффициенты, равноудаленные от начала и конца разложения, равны между собой  ,p=0,1,2,…,n; ; сумма биномиальных коэффициентов равна числу2, возведенному в степень, равную показателю степени бинома Ньютона:  ; сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах. Первые два свойства являются свойствами числа сочетаний. Перестановки, размещения, сочетания с повторениями. Перестановка – _ Размещение- Сочетание- 7. Признак клеток (Дирихле). Принцип Дирихле — простой, интуитивно понятный и часто полезный метод для доказательства утверждений о конечном множестве. Этот принцип часто используется в дискретной математике, где устанавливает связь между объектами («кроликами») и контейнерами («клетками») при выполнении определённых условий. В английском и некоторых других языках данное утверждение известно как «принцип голубей и ящиков, когда объектами являются голуби, а контейнерами — ящики.Этот принцип утверждает, что если множество из n элементов разбито на m непересекающихся частей, не имеющих общих элементов, гдеn > mто, по крайней мере, в одной части будет более одного элемента.На языке отображений эта формулировка означает, чтоесли в А (множестве предметов) больше элементов, чем в В (множестве ящиков), то не существует обратимого отображения А в В.Другая формулировка “ принципа Дирихле“:если n + 1 предмет поместить в n мест, то обязательно хотя бы в одном месте окажутся хотя бы двапредмета.В шутливой форме принцип Дирихле выглядит так: “нельзя посадить семерых зайцев в три клетки так, чтобы в каждой клетке находилось не больше двух зайцев “. [2] Признак математической индукции. Индукция – это переход от частного к общему, а дедукция наоборот – от общего к частному. Определение 2 9. Высказывания. Отрицание, конъюнкция, дизъюнкция, их таблицы истинности.Высказываниемназывается повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно.Например, «Москва – столица России», «число 2 больше 5» – высказывания. Первое высказывание является истинным, а второе – ложным.Отрицаниемвысказывания  называется высказывание («не », «неверно, что »), которое истинно, когда ложно, и ложно, когда истинно.Таблица истинности для отрицания: Конъюнкцией (логическим умножением) двух высказываний  , называется высказывание (« и »), которое истинно только в том случае, когда и оба истинны.Таблица истинности для конъюнкций: Дизъюнкцией (логическим сложением) двух высказываний  , называется высказывание (« или »), которое истинно, когда хотя бы одно из них истинно.Таблица истинности для дизъюнкций: 10. Импликация и эквиваленция, таблицы их истинности.Импликацией двух высказываний  ,  называется высказывание  («если , то », « влечёт », «из следует », « имплицирует »), которое ложно тогда и только тогда, когда истинно, а ложно.Таблица истинности для импликаций:  Эквивалентностью высказываний  , называется высказывание (« эквивалентно », « тогда и только тогда, когда », «для того, чтобы , необходимо и достаточно, чтобы »), которое истинно тогда и только тогда, когда  и  оба истинны или ложны.Таблица истинности для эквивалентности: 11. Эквивалентные высказывания. Теорема о свойствах логических эквивалентностей.Эквиваленцией (или эквивалентностью) двух высказываний Х, У называется новое высказывание, которое считается истинным, когда оба высказывания Х, У, либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.Эквиваленция высказываний Х, У обозначается символом  (или,

22. Булева алгебра.Булевой алгеброй называется дистрибутивная структура с неравными друг другу единицей 1 и нулем 0, в которой всякий элемент имеет дополнение. Булева алгебра всегда содержит не менее двух элементов. Алгебра, содержащая только 1 и 0, называется вырожденной.23. Основные законы и свойства операций Булевой алгебры.Как любая алгебраическая система булева алгебра базируется на совокупности некоторых предположений, которые принято называть аксиомами, т.е предположениями не требующими доказательств. Аксиомы определяются для двух логических значений 1 ( "ИСТИНА" ) и 0 ( "ЛОЖЬ" ) и операций логического умножения (конъюнкции), которая обозначается " & ", " · " или не обозначается вовсе, логического сложения (дизъюнкции), которая обозначатся " v ", "+", и отрицания ( инверсии ), которая обозначается горизонтальной чертой (" - ") над переменной или выражением, например, . Булевой переменной, обозначаемой обычно xi , называется переменная принимающая два логических значения { 0, 1 }.Ниже приведены аксиомы булевой алгебры относительно дизъюнкции, конъюнкции и отрицания.Аксиомы конъюнкции 0·* 0 = 0 ; 1·* 1 = 1 ; 0·* 1 = 1·* 0 = 0 ;Аксиомы дизъюнкции 0 v 0 = 0 ; 1 v 1 = 1 ; 0 v 1 = 1 v 0 = 1 ;Аксиомы отрицания Если x = 0 , то ˆх = 1 ;Если x = 1 , то ˆх = 0 ;Следующие 5 правил обычно называют теоремами булевой алгебры. Особенностью теорем булевой алгебры является то, что для их доказательства пользуются простой подстановкой значений булевых переменных. Это обусловлено тем, что переменные могут принимать только 2 значения - 0 и 1.Операции с константами : Идемпотентность (тавтология, повторение) :  Для n переменных:  Противоречие :Правило "исключенного третьего" :Двойное отрицание (инволюция) :Следующие 4 правила обычно называют законами или тождествами булевой алгебры.Ассоциативность ( ассоциативный закон ) :   Коммутативность ( коммутативный закон ) :   11. Дистрибутивность ( дистрибутивный закон ) :конъюнкции относительно дизъюнкции: дизъюнкции относительно конъюнкции: 24. Отношения множеств. Область определения и множество значений отношения. Обратное отношение. Область определения отношения R – это подмножество всех элементов х множества Х, для которыхнайдется элемент y, связанный с данным элементом отношением R. Область значения отношения R – подмножество всех элементов y множества У, для которых найдутся элементы x, связанные с y отношением R (). Пример: Если область определения отношения совпадает с некоторым множеством X, то говорят, что отношение определено на X. Итак, если R — отношение на множестве X, то R X X. Множество всех первых элементов пар из R называется областью определения отношения R. Множеством значений отношения R называется множество всех вторых элементов пар из R. Обратное отношение (отношение, обратное к R) — это двухместное отношение, состоящее из пар элементов (у, х), полученных перестановкой пар элементов (х, у) данного отношения R. Обозначается: R−1. Для данного отношения и обратного ему верно равенство: (R−1)−1= R. Взаимо-обратные отношения(взаимообратные отношения) — отношения, являющиеся обратными друг по отношению к другу. Область значений одного из них служит областью определения другого, а область определения первого — областью значений другого. 25. Специальные свойства отношений на А. Частично упорядоченные множества.Бинарным отношением на множестве А называется подмножество его квадрата RÍ A2. Бинарным отношением между множествами А и В называются подмножество принадлежащее декартовому произведению 2-х множеств: RÍ АхВ.Если упорядоченная пара (а1, а2) принадлежит отношению R, то говорят что а1 R а2, то есть между элементом а1 и а2 уст-но отношение R.Областью определения бинарного отношения называется множество элементов а, в котором в принадлежит бинарному отношению: þR={a|bÎ aRb}.Областью значения бинарного отношения называют множество b, в котором а принадлежит бинарному значению:PR={b|aÎ aRb }.Обратное отношение для отношения R называется отношение: R-1={(b,a)|(a,b) Î R }.Отношение можно задать:-с помощью любого способа задания множеств-С помощью матрицы бинарного отношения. Матрица бинарного отношения это квадратная матрица R элементы которой определяются следующим образом rij=1, (ai,aj)Î R, 0 – в противном случае.-С использованием графа. Каждому бинарному отношению можно подставить в соответствие граф G(X,U), содержащий множество вершин Х, и множество ребер U. При этом вершины ajai соединяются дугой если упорядоченная пара ajai Î R. Так как отношения являются множеством упорядоченных пар, то для отношения можно определить те же операции, что и для множеств (объединение, пересечение, разность, дополнение, симметрическая разность).

Взвешенные графы

Ремарка




48. Объединение, пересечение, дополнение графов.
Пересечение (произведение) графовПересечением графов G1(X1,Г1X1) и G2(X2,Г2X2) называется такой граф G(X,ГX), у которого множество вершин есть пересечение множеств вершин графов X=X1ÇX2, а отображение есть пересечение отображений перемножаемых графовГX=Г1X1ÇГ2X2.Пример.Пересечение графов G1 и G2 предыдущего примера есть граф G(X,ГX)



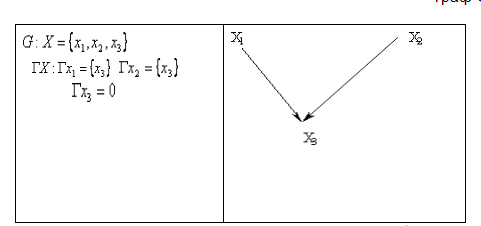
Объединением графов G1(X1,Г1X1) и G2(X2,Г2X2) называется такой граф G(X,ГX), у которого множество вершин есть сумма множеств вершин объединяемых графов X=X1ÈX2, а отображение есть сумма отображений объединяемых графовГX=Г1X1ÈГ2X2. обозначает: G=G1ÈG2.

Пример. Заданы графы G1и G2:



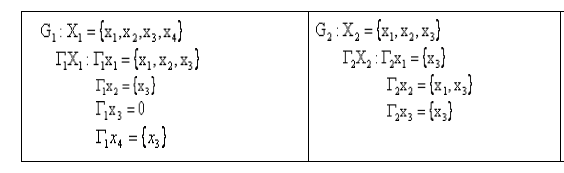
  1. Дополнениемграфа G1(V1,E1) называется граф G2(V2,E2), у которого множество вершин такое же, как у исходного графа, а множество ребер представляет собой дополнение до множества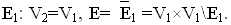   Вершины графа G2смежны только в том случае, когда они не смежны в исходном графе. Обозначение: ` G1(V1,E1). Дополнение графов есть дополнение

Дополнение к полному графу – пустой граф. Другой пример показан на рисунке.


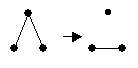
49. Разрезающее множество, разрезающее ребро и разрезающая вершина графа.

К Разрезающиму множеству S связного графа G относится такое минимальное множество ребер графа G что удаление их из графа
G разделяет последний т.е г раф G-S становиться не связным.



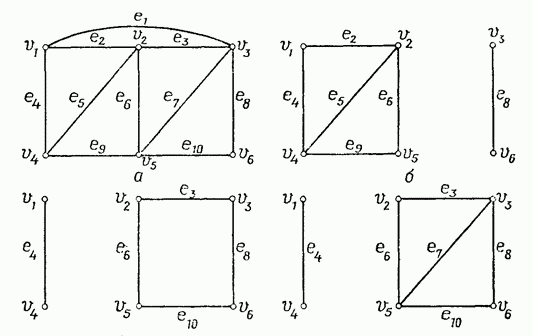
 Ребро е графа G является разрезающим тогда и только тогда, когда оно не входит в цикл графа G.

Разрезающая вершина(Cutvertex (cuttingvertex)) —вершина   графа   такая, что после ее удаления множество   разбивается на непересекающиеся непустые подмножества   и  , между которыми нетреберграфа  .
50. Теоремы о компонентах двусвязности графа.

Компонентой двусвязности графа называется такое максимальное подмножество из трех или более его вершин, в котором любые две вершины соединены, по крайней мере, двумя путями, не имеющими общих ребер. 

 Кроме того компонента двусвязности может представлять собой просто две вершины, соединенные одним ребром. Компонента двусвязности - устойчивая часть графа: если в ней удалить вершину и все примыкающие к ней ребра, то любые две из оставшихся вершин по-прежнему оказываются соединенными между собой.

51. Планарные графы. Грани. Формула Эйлера.

Граф, который может быть изображенна плоскостибез пересечений рёбер, называетсяпланарным графом.

Например, граф

G({a,b,c,d},{{a,b}{a,c}{a,d}{b,c}{b,d}{c,d}})

можно изобразить и с пересечением и без пересечений рёбер, поэтому этот граф является планарным.



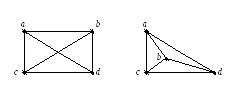
Если граф планарный и изображен на плоскости без пересечений рёбер, то диаграмма для графа разделяет плоскость на части, называемые
гранями.Грань – максимальный участок плоскости, в котором две точки могут быть соединены линией (любой формы), не пересекающей ребро графа.



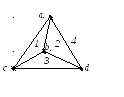
На рисунке три грани изображены треугольниками:1 – abc,2 – abd,3 – bcd. Грань4представляет собой внешнюю область плоскости.

Формула Эйлера. В связном планарном графе v − e + f = 2.
52. Теоремы о планарных и непланарных графах.

Если G связный плоский граф имеющий р –вершин и q- ребер и f –граней то p+f-q=2 данная теорема называется формулой эйлера

53. Непланарность графа Петерсона.



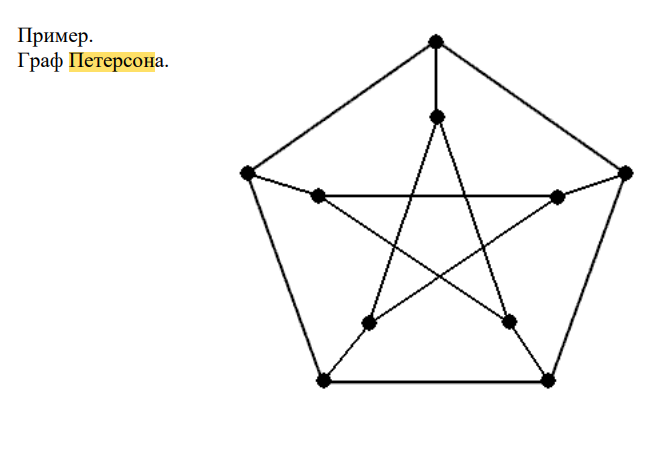
Т.к. в графе Петерсона степени всех вершин равны 3, найти подграф, гомеоморфный K5 , нельзя. Следовательно, существует подграф, гомеморфный K3,3 . Будем использовать следующий образец для выбора вершин на роль вершин одной доли (1, 2, 3) и на роль вершин второй доли (4, 5, 6).

54. Гамильтонов путь и Гамильтонов цикл. Теоремы о Гамильтоновых циклах.

Если граф имеет простой цикл, содержащий все вершины графа по одному разу, то такой цикл называется гамильтоновым циклом, а граф называется гамильтоновым графом. Граф, который содержит простой путь, проходящий через каждую его вершину, называется полугамильтоновым. Это определение можно распространить на ориентированные графы, если путь считать ориентированным.

Гамильтовым путем называется граф проходящий через каждую его вершину только один раз.

Теорема Дирака. Если в графе G(V, E) с p ≥ 3 вершинами ∀v ∈ V d(v) ≥ p/2, то граф G является гамильтоновым. Доказательство. Пусть V = {v1, . . . , vp}. Заметим сначала, что любой граф можно превратить в гамильтонов добавлением в него p дополнительных вершин степени 2: вместе с дополнительной вершиной ui , где i = 1, . . . , p − 1 добавляются ребра (vi , ui) и (ui , vi+1), вместе с вершиной up – ребра (vp, up) и (up, v1). Тогда гамильтонов цикл имеет вид:

v1u1v2u2 . . . vpupv1.
55. Замыкание графа. Примеры.



ПРИМЕР



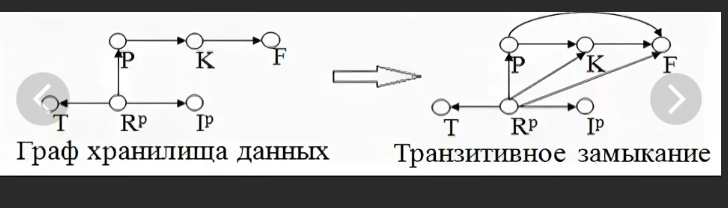
56. Взвешенные графы. Алгоритм Дейкстры.


Взвешенные графы


В классических графах все рёбра считаются равноценными и длина пути соответствуетколичествурёбер, которые он содержит. Однако часто в задаче каждому ребру соответствует некоторый параметр -длинаребра илистоимостьпрохождения по нему. В терминологии графов такой параметр называетсявесомребра, а граф, содержащий взвешенные рёбра,взвешенным.



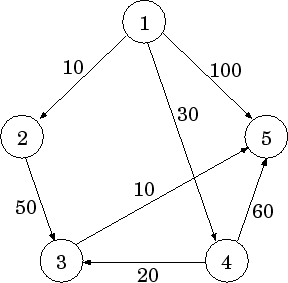
Типичная задача для таких графов - поиск кратчайшего пути. Например, в этом графе кратчайший путь между вершинами11и55:1−4−3−51−4−3−5, так как его вес равен30+20+10=6030+20+10=60, а вес ребра1−51−5равен100100.

Классический алгоритм для поиска кратчайших путей во взвешенном графе - алгоритм Дейкстры (по имени автора Эдгара Дейкстры). Он позволяет найти кратчайший путь от одной вершины графа до всех остальных заO(MlogN)�(�log⁡�)(N,M�,�- количество вершин и рёбер соответственно).

Принцип работы алгоритма напоминает принцип работы BFS: на каждом шаге обрабатывается ближайшая ещё не обработанная вершина (расстояние до неё уже известно). При её обработке все ещё не посещённые соседи добавляются в очередь для посещения (расстояние до каждой из них рассчитывается как расстояние до текущей вершины + длина ребра). Главное отличие от BFS заключается в том, что вместо классической очереди используется очередь с приоритетом. Она позволяет нам выбирать ближайшую вершину заO(logN)�(log⁡�).

Анимация выполнения алгоритма Дейкстры для поиска кратчайшего пути из вершиныa�в вершинуb�:

С помощью псевдокода алгоритм Дейкстры описывается следующим образом:

ans = массив расстояний от начальной вершины до каждой.

изначально заполнен бесконечностями (ещё не достигнута).

Смотрите также файлы