Файл: Методические указания к выполнению лабораторной работы 232а по курсу Общая физика для студентов всех специальностей Составитель.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 61
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
министерство образования и науки российской федерации Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Утверждаю
Проректор-директор
О.Ю. Долматов
« » 2013 г.
Сложение взаимно перпендикулярных гармонических колебаний (фигуры Лиссажу)
Методические указания к выполнению лабораторной работы 2-32а
по курсу «Общая физика» для студентов всех специальностей
Составитель Д.Н. Краснов
Издательство
Томского политехнического университета
2013
УДК 000000
ББК 00000
М00
Сложение взаимно перпендикулярных гармонических колебаний (фигуры Лиссажу): методические указания к работе 2–32а по курсу «Общей физики» для студентов всех специальностей / сост. Д.Н. Краснов; Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2013. – 18 с.
УДК 000000
ББК 00000
Методические указания рассмотрены и рекомендованы
к изданию методическим семинаром кафедры
общей физики ФТИ
«»2013 г.
Зав. кафедрой ОФ
кандидат физ.-мат. наук, ___________ А.М. Лидер
Председатель
учебно-методической комиссии ___________ Т.В. Смекалина
Рецензент
Доктор педагогических наук,
профессор кафедры ОФ ФТИ НИ ТПУ
В.В. Ларионов
© Составление. ФГБОУ ВПО НИ ТПУ, 2013
© Д.Н. Краснов, составление, 2013
Цель работы: изучение сложения взаимно перпендикулярных гармонических колебаний, определение отношения частот колебаний по виду фигур Лиссажу, исследование влияния разности фаз колебаний на вид фигур Лиссажу.
Приборы и принадлежности: электронный осциллограф GDS-71022, генераторы сигналов ГЗ-131.
Теоретическое введение
Общие сведения о гармонических колебаниях
Колебательные явления играют важную роль в самых разнообразных вопросах физики. Рассмотрим случай простых или гармонических колебаний. Характер такого движения лучше всего раскрывается с помощью следующей кинематической модели. Допустим, что материальная точка
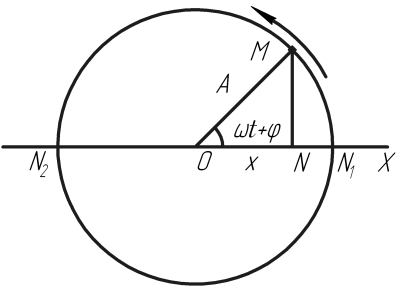
Рис. 1.1. Схема простого колебательного движения
Ее проекция
Полученная формула описывает аналитически гармоническое колебательное движение точки
вдоль диаметра
Величина
Для графического изображения гармонического колебательного движения по оси
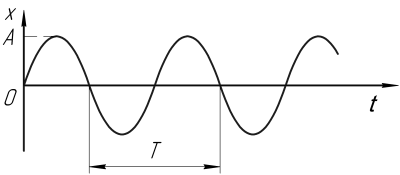
Рис. 1.2. Графическое представление гармонического колебательного движения
Форма кривой полностью определяется амплитудой
фаза получает приращение
Скорость колеблющейся точки найдется дифференцированием выражения (1) по времени. Это дает
(3)
Дифференцируя вторично, получаем ускорение
Сравнивая (1) и (4), получим
Это уравнение называется уравнением гармонических колебаний.
В общем случае, физическая величина
Сложение взаимно перпендикулярных колебаний
Рассмотрим гармоническое колебательное движение материальной точки, осуществляющееся одновременно в двух взаимно перпендикулярных направлениях. Пусть одно колебание происходит по оси
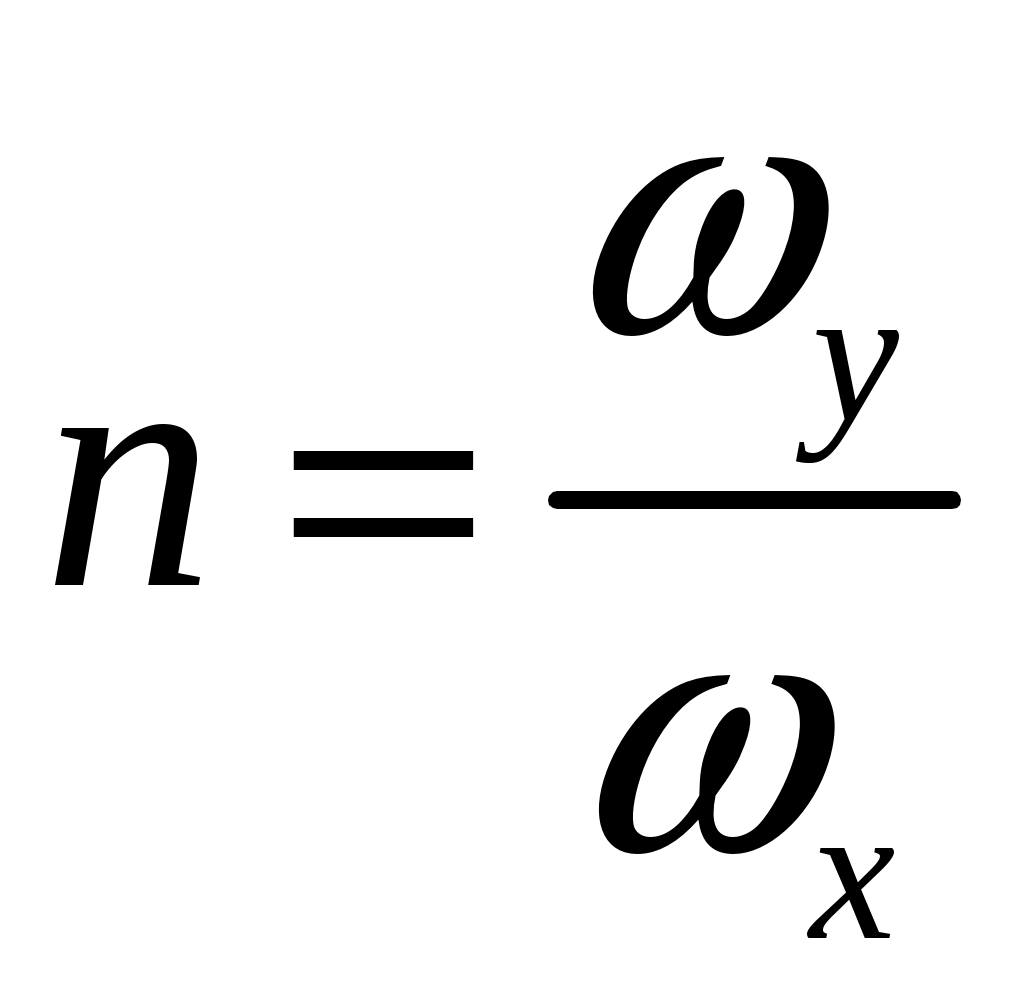 ,
,где
Система уравнений (6), (7) представляет собой уравнение кривой, являющейся результатом сложения этих колебаний, заданной в параметрической форме. Определим уравнение траектории точки, участвующей в данных колебаниях, решая систему уравнений (6) и (7), исключая из уравнения (7) время
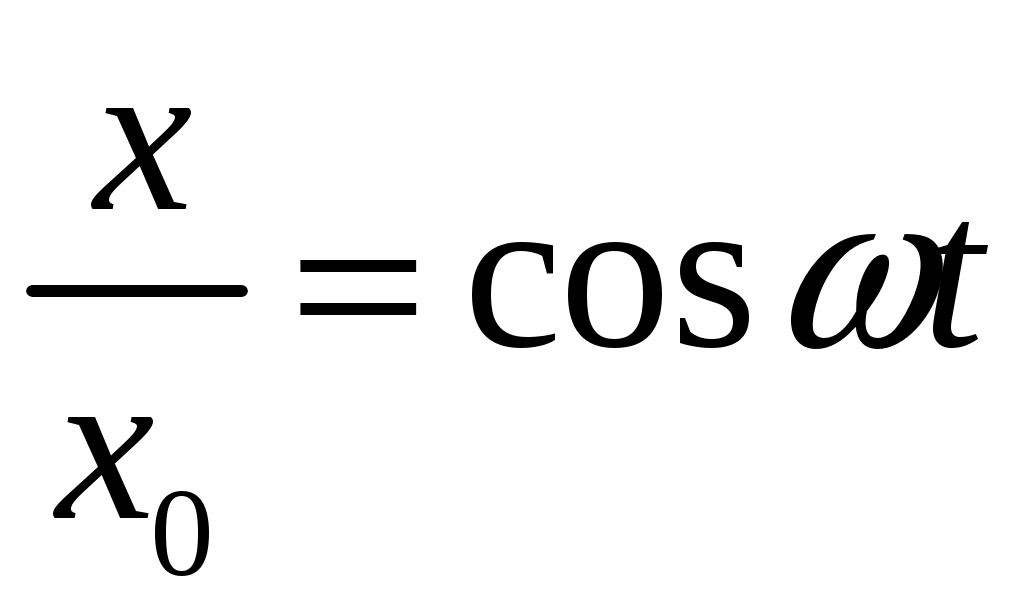 (8)
(8)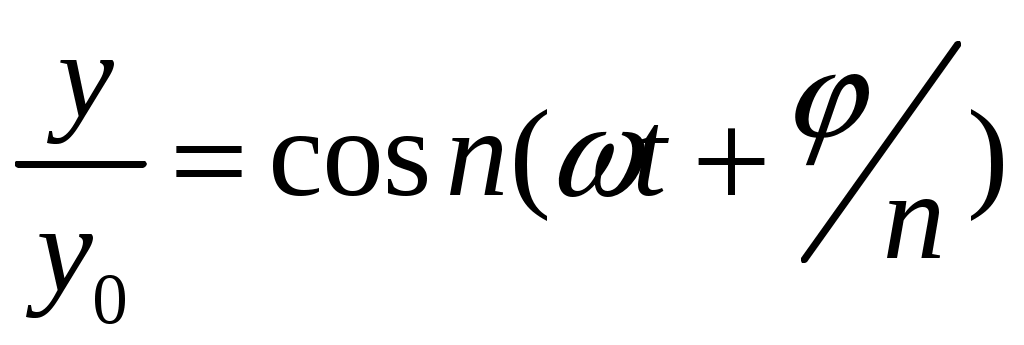 (9)
(9)Прибавим к левой и правой части (9) мнимую величину
получим
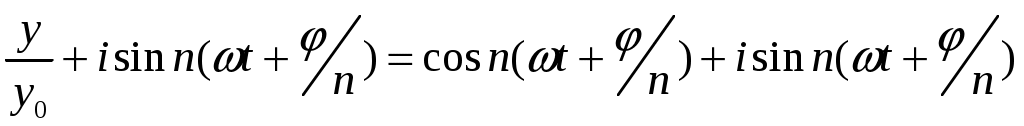 (10)
(10)По формуле Муавра:
Тогда
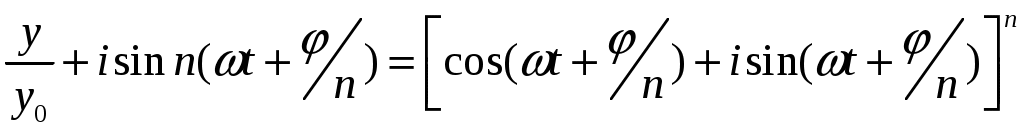 (12)
(12)Или
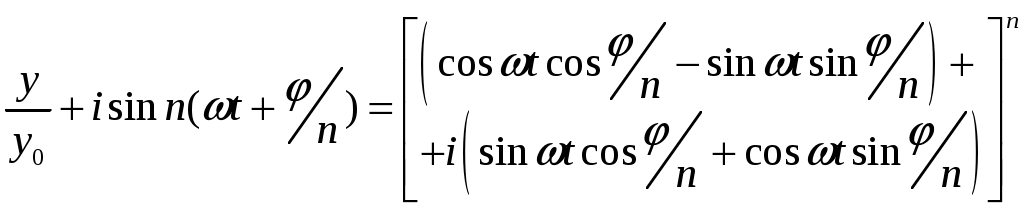 (13)
(13)Но
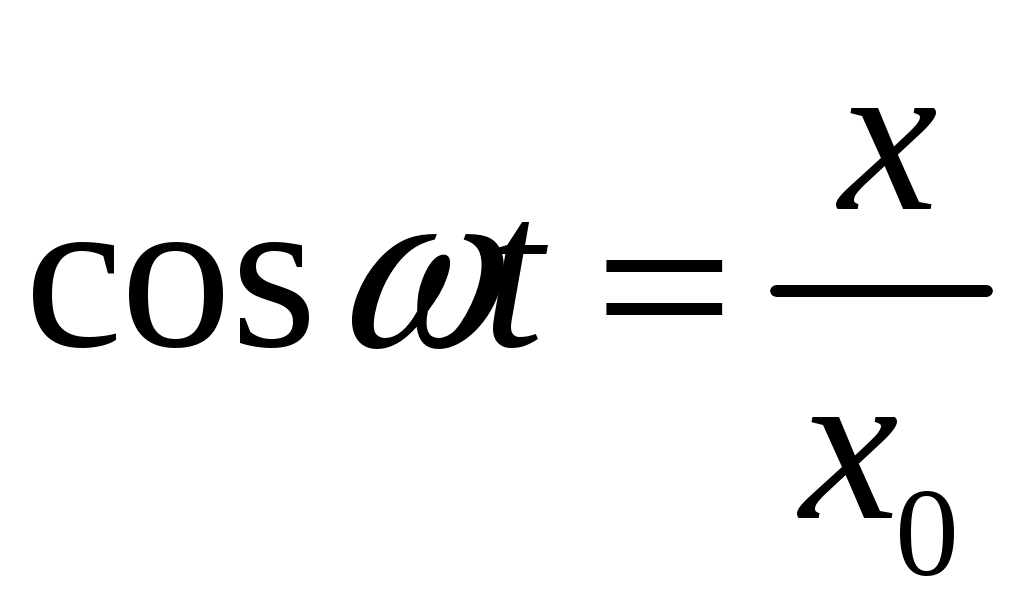 ,
, 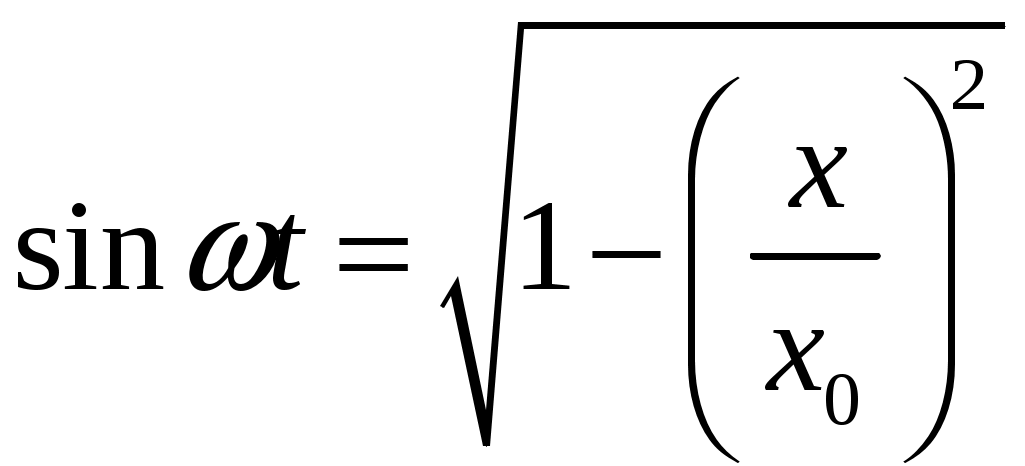 . Подставляя эти значения в формулу (13), получим:
. Подставляя эти значения в формулу (13), получим: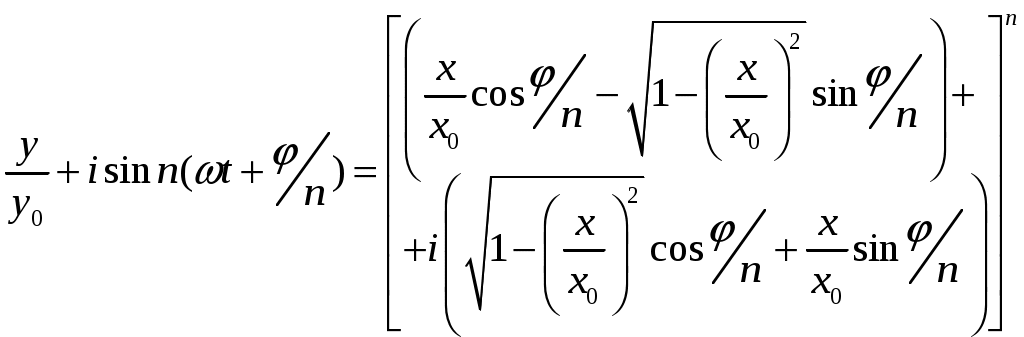 (14)
(14)Разлагая по биному Ньютона (n – целое число) выражение в квадратных скобках и приравнивая действительные части слева и справа, получим уравнение траектории колеблющейся точки. Рассмотрим частный случай – сложение колебаний с одинаковыми частотами (n=1). Из формулы (14) получим:
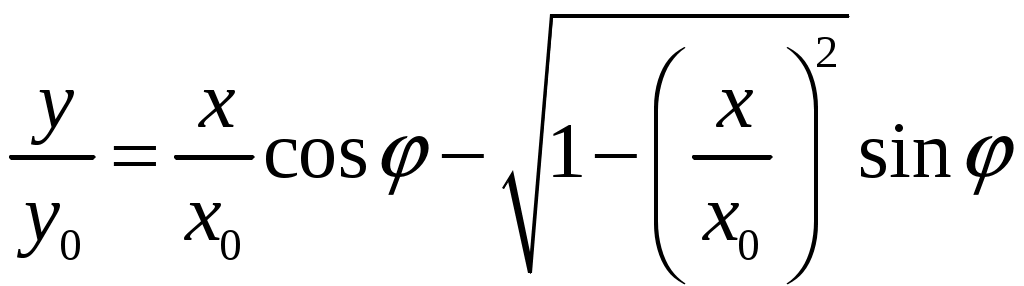 (15)
(15)Откуда:
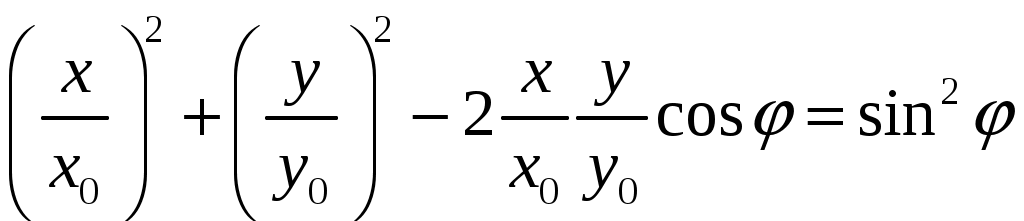 (16)
(16)Это уравнение является в общем случае уравнением эллипса.
Рассмотрим ряд частных случаев.
-
Пусть колебания происходят в одинаковых фазах, т.е.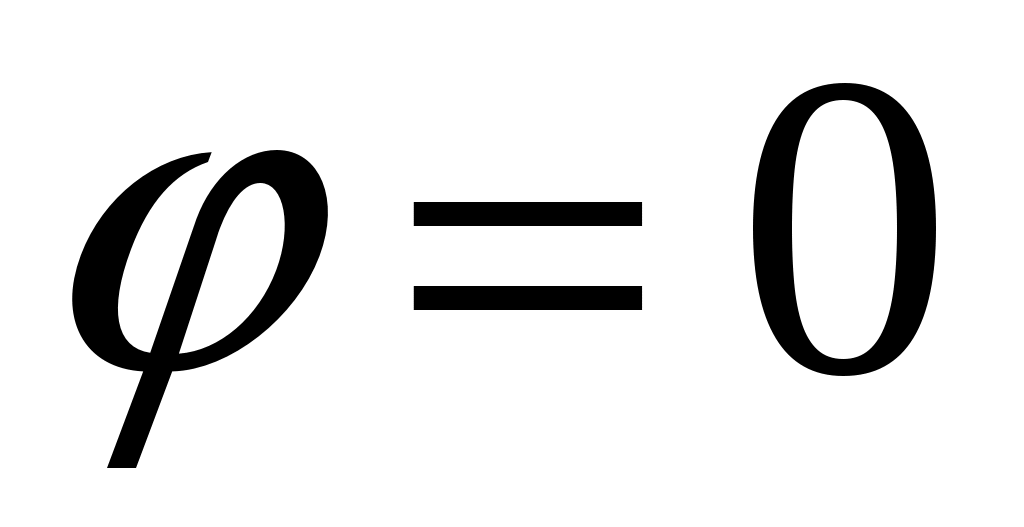 . В этом случае уравнение (16) принимает вид:
. В этом случае уравнение (16) принимает вид:
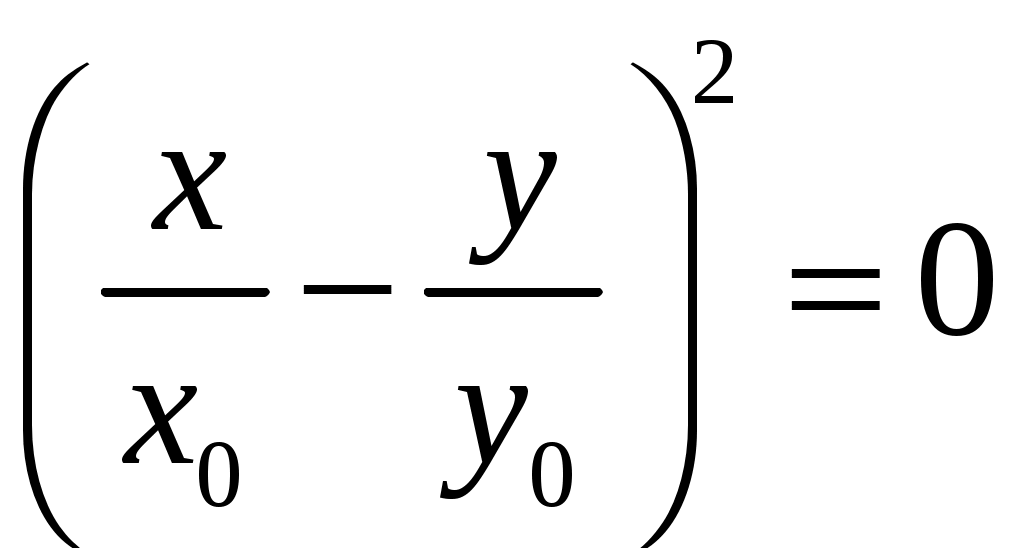 (17)
(17)или
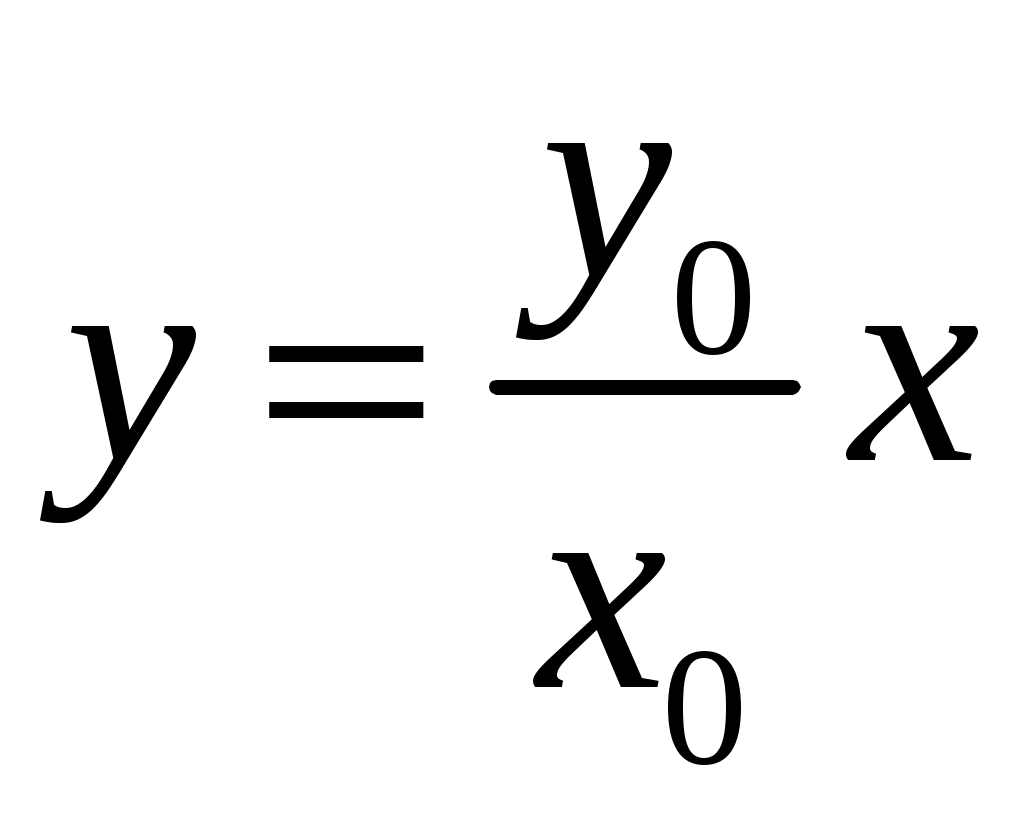 (18)
(18)Это есть уравнение прямой с углом наклона
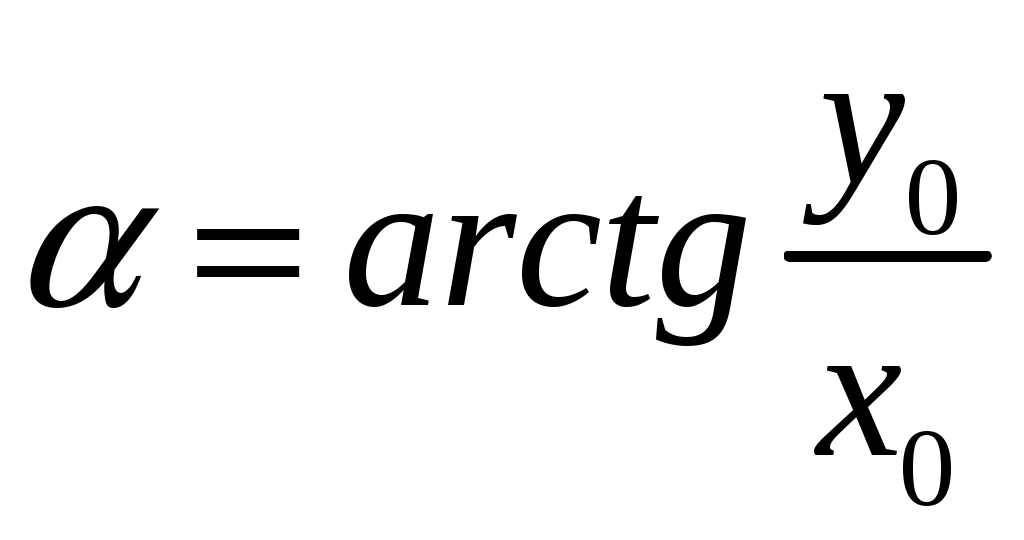 .
.Если разность фаз
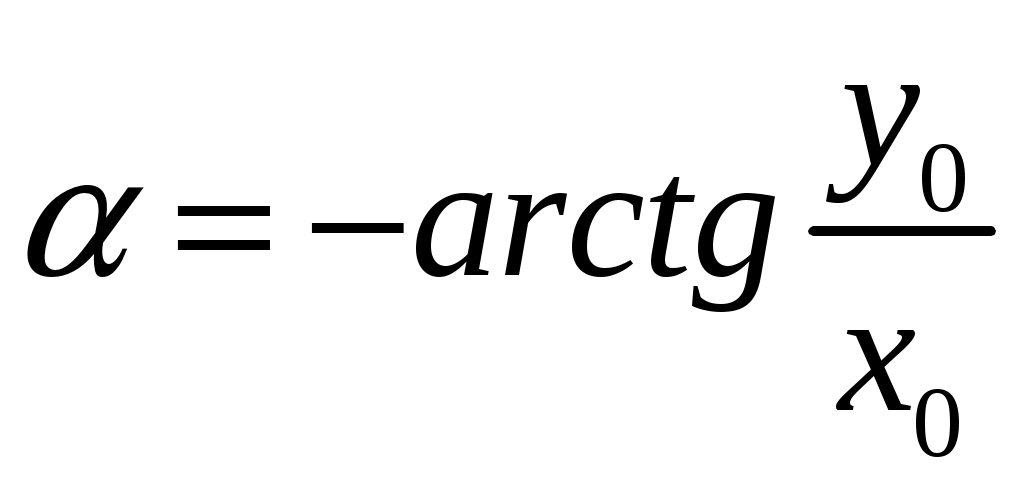 .
.-
Пусть разность фаз между колебаниями равна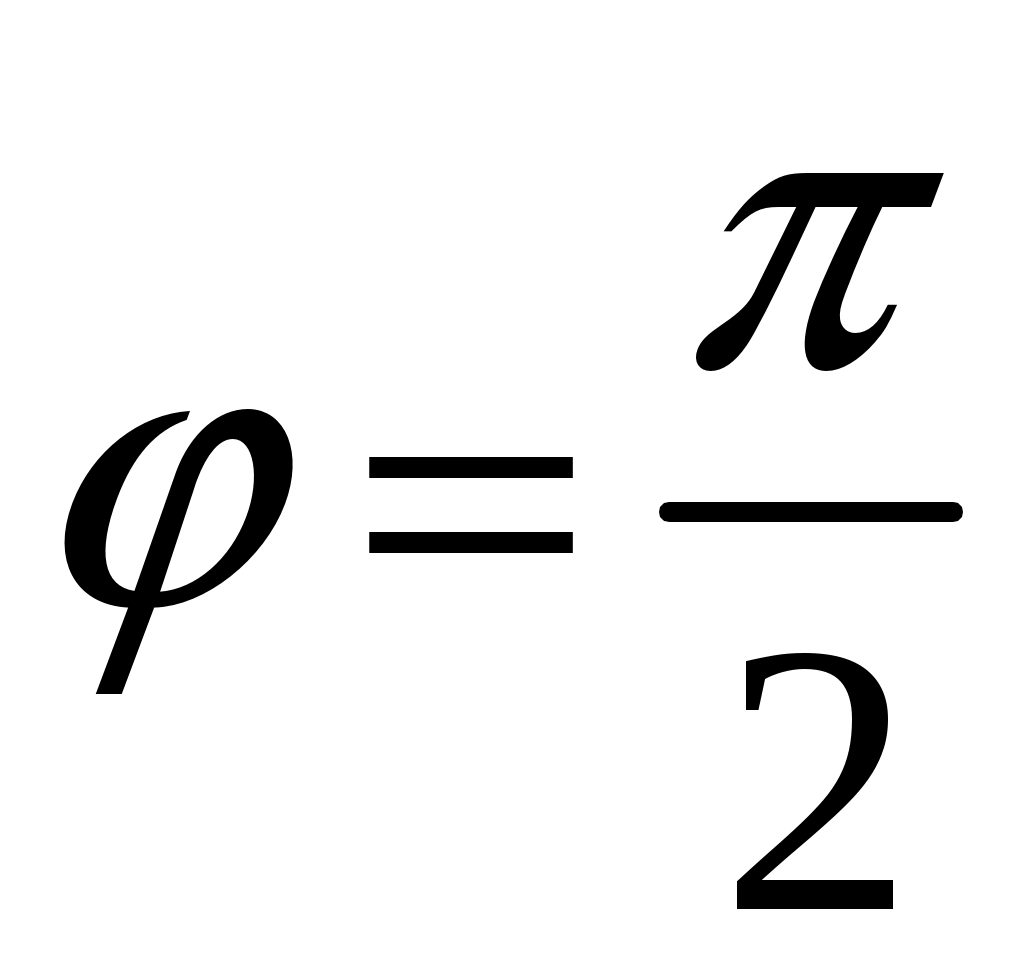 . Тогда уравнение (7) будет иметь вид:
. Тогда уравнение (7) будет иметь вид:
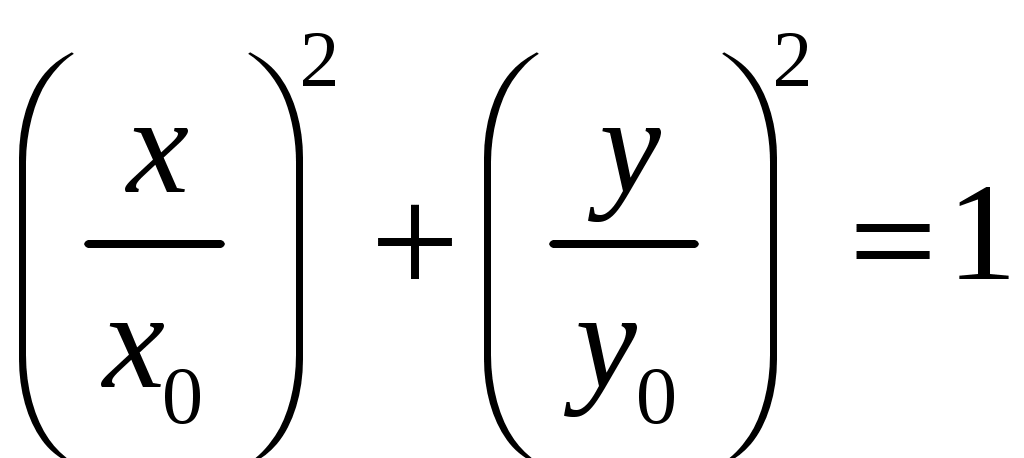 (19)
(19)Полученная кривая является эллипсом, оси которого совпадают с осями координат.