Файл: Разработка многоканальной системы связи.docx

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ВОЗДУШНОГО ТРАНСПОРТА

(РОСАВИАЦИЯ)

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ» (МГТУ ГА)

Кафедра основ радиотехники и защиты информации (ОРТЗИ)

Курсовая работа

по дисциплине “Теория электрической связи”

Тема: “Разработка многоканальной системы связи”

Вариант № 29

Выполнил:

Студент 3 курса

Группы

Руководитель:

Москва 2023

Аннотация

Системы передачи информации используются во многих отраслях. В
зависимости от назначения, они должны отвечать определенным требованиям:и отказоустойчивость, помехоустойчивость и пропускная способность.

Эта курсовая работа посвящена расчету и анализу основных характеристик многоканальной дискретной системы связи. Основная задача – разработать многоканальную когерентную систему передачи дискретной информации, предназначенную для передачи цифровых сигналов.

Задание и исходные данные

Исходные данные

Задание: разработать обобщенную функциональную и электрическую функциональную схему многоканальной системы связи и рассчитать её основные тактико-технические характеристики.

Исходные данные:

Число каналов	2
Длина кодовой комбинации (слова) на входе канала (бит)	4
Суммарная средняя мощность сигнала на входе приемника 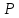, (пВт)	3Е-4
Средняя скорость на входе канала, (слова/с)	3
Тип манипуляции	ЧМ
Способ уплотнения каналов	ВУ
Степень когерентности системы	Некогерентная
Спектральная плотность мощности шума на входе приемника 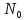, (пВт/Гц)	1Е-6
Тип корректирующего кода	Хэмминга (15,11)

Содержание

Аннотация 3

1.Задание и исходные данные 4

2.Расчёт технических параметров проектируемой СПИ и обоснование технических требований к её элементам. 6

2.1 Назначние СПИ 6

2.2 Выбор численных значений параметров корректирующего кода, при которых обеспечивается минимальная битовая вероятность ошибки на выходе декодера. 6

2.3 Листинг программы кодирования и декодирования для персонального компьютера (ПК) на языке программирования Python 11

2.4 Вычисление вероятности ошибки при приеме кодового слова и битовой вероятности ошибки на выходе декодера и оценка частоты появления ошибок 14

2.5 Выбор способов введения и численных значений параметров синхросигналов 14

3.Разработка функциональной схемы системы в целом для передачи в одном направлении 17

Заключение 19

Список используемой литературы 20

Расчёт технических параметров проектируемой СПИ и обоснование технических требований к её элементам.

2.1 Назначние СПИ

Определяя предполагаемое назначение СПИ, нужно учитывать скорость передачи в одном канале и количество двоичных разрядов в кодовой комбинации. Скорость передачи информации в одном канале равна:

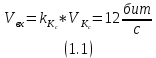
Такая скорость передачи информации является недостаточной для случая радиолокационного измерения расстояния до летящей ракеты, но является уместной для передачи значений направления и скорости ветра при метеорологических наблюдениях или скорости движения конвейера.

Количество разрядов в кодовой комбинации k определяет относительную величину модуля максимальной ошибки:

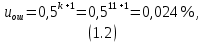
Величина модуля максимальной ошибки в данном случая не подходит для передачи значений координат движущегося объекта, однако достаточна для передачи данных о направлении и скорости ветра.

2.2 Выбор численных значений параметров корректирующего кода, при которых обеспечивается минимальная битовая вероятность ошибки на выходе декодера.

Коды Хэмминга – это простой класс блочных кодов, которые имеют следующую

структуру:

⁽????, ????⁾= ⁽2^???? − 1, 2^???? − 1 − ????⁾,

(2.1)

где ???? = 2,3,4, … - основание блочного кода, ???? – число бит кодового слова, ???? –

число информационных бит.

Число проверочных бит кода:

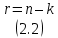
Избыточность кода:

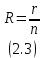
Способности кода к обнаружению ???? ошибок и исправлению ???? ошибок определяются:

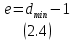
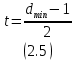
При минимальном расстоянии Хэмминга ????_????_????_????_???? = 3 получим ???? = 1 и ???? = 2 – т.е код способен исправить все однобитовые ошибки или определить все модели ошибки из двух или малого числа ошибок в блоке (слове).

Вероятность появления битовой ошибки:

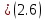
где ???? – кратность ошибки, кол-во неверно принятых символов в блоке (слове),

????кс – вероятность ошибочного приёма канального символа (кодового слова)

????_????. В частности, для кодов Хэмминга вместо уравнения (3.9) можно использовать

другое эквивалентное уравнение:

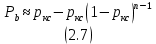Для описания гауссовского канала с использованием когерентной бинарной фазовой манипуляции, вероятность ошибочного приёма канального символа (кодового слова) можно выразить через соотношение:

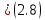
где ????_к_????^⁄????₀ – отношение энергии кодового символа к спектральной плотности мощности шума, ????(????) – Гауссов интеграл ошибок, определён в [приложение А].

Чтобы связать ????к????/????0 с энергией бита информации на единицу плотности спектрального шума (????????/????0), используем:

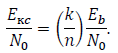(2.9)

Для кодов Хэмминга уравнение (3.12):

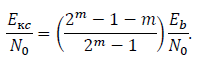(2.10)

Среднее время безошибочной работы в групповом канале передачи данных

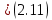
где ????_д _вых – битовая вероятность появления ошибки на выходе декодера, ^〈????^〉-

средняя скорость источника информации.

Рассчитаем параметры помехоустойчивого кодирования при различных значениях основания кода ????.

Для ???? = ????:

⁽????, ????⁾= ⁽2^???? − 1,2^???? − 1 − ????⁾= ⁽2² − 1,2² − 1 − 2⁾= ⁽3,1⁾;

???? = ???? − ???? = 3 − 1 = 2;

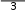???? = ^????⁻^????= ³⁻¹= 0,67.

Согласно формуле (3.13), получим:

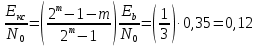
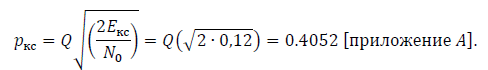
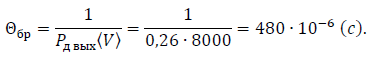
^Для ???? = ????:

⁽????, ????⁾= ⁽2^???? − 1,2^???? − 1 − ????⁾= ⁽2³ − 1,2³ − 1 − 3⁾= ⁽7,4⁾;

???? = ???? − ???? = 7 − 4 = 3;

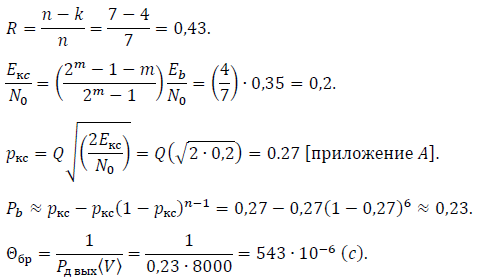
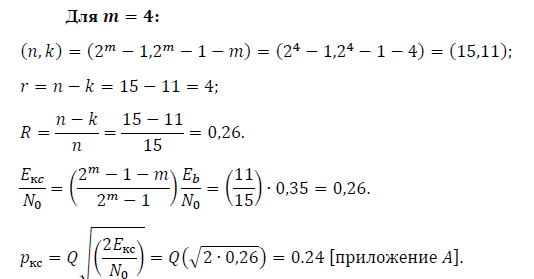
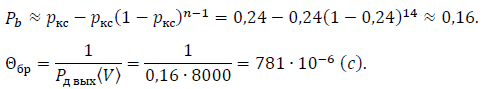
Как показали расчёты вероятность появления битовой ошибки ????_???? при кодировании кодами Хэмминга тем меньше, чем больше основание кода ????, т.е чем большее количество проверочных символов вводится в информационный сигнал.

2.3 Листинг программы кодирования и декодирования для персонального компьютера (ПК) на языке программирования Python

Ниже представлен код на языкуе Python кодера и декодера кода Хэмминга:

import numpy as np

# функция, которая возвращает биты проверки ошибок

def get_check_bits(data):