Файл: Методы решения задач на смеси и сплавы.docx

Муниципальное казенное общеобразовательное учреждение "Средняя общеобразовательная школа № 1 имени Героя Советского Союза М. А. Машина"

ИНДИВИДУАЛЬНЫЙ ПРОЕКТ

«Методы решения задач на смеси и сплавы»

Автор: Полыгин Алексей Федорович

учащийся 11-А класса

Руководитель: Жданова Ольга Анатольевна

Допуск к защите

_______________________________________________________

Г. Лиски

2023г.

Паспорт проекта

(Индивидуальный план выполнения проекта)

Этапы	Виды деятельности
Подготовительный	Выбор темы проекта, которая заинтересовала меня больше всего.
Поисковый (исследовательский)	изучение выбранной темы, поиск и выбор самой важной информации.
Аналитический (Процесс проектирования)	Оформление проекта: систематизирование всех полученных данных в одну работу. Исправление недочетов.
Презентация полученного результата(продукта).	Защита проекта.

Для руководителей проекта

Общие сведения

№ п/п	ФИО ученика	Тема проекта	Руководитель	Итоговая оценка	Подпись ученика
1.	Полыгин Алексей Федорович	Методы решение задач на смеси и сплавы	Жданова Ольга Анатольевна

Оглавление

---

1. Введение

Человеку часто приходится смешивать разные жидкости, порошки, газообразные или твёрдые вещества или разбавлять что-то водой. Поэтому в современном мире множество отраслей, например таких, как пищевая, фармацевтическая, тяжёлая промышленность, связаны с химией. Впервые в вариантах единого государственного экзамена по математике задача на «смеси и сплавы» появились в 2003 году в заданиях группы В

2. История появления процентов в жизни

Само слово «процент» происходит от лат. «pro centum», что означает в переводе «сотая доля». В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.

В Древнем Риме были широко распространены денежные расчеты с процентами. Римский сенат установил максимально доступный процент, взимавшийся с должника.

От римлян проценты перешли к другим народам Европы.

Есть мнение, что понятие «процент» ввел бельгийский ученый Симон Стевин. В 1584 г. он опубликовал таблицы процентов.

Употребление термина «процент» в России начинается в конце XVIII в. Долгое время под процентами понималось исключительно прибыль или убыток на каждые 100 рублей. Проценты применялись только в торговых и денежных сделках. Затем область их применения расширилась.

В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento).

Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.(Рис.1)

Рис. 1.

3. Основные термины и понятия при решении задач.

Концентрация вещества – это отношение массы или объема вещества к массе или объему всего раствора. Как правило, концентрация выражается в процентах.

Масса раствора равна сумме масс всех составляющих.

При смешивании нескольких растворов (смесей, сплавов) масса нового раствора становится равной сумме всех смешанных растворов.

---

Масса растворенного вещества при смешивании двух растворов суммируется.

4. Способы решения задач на смеси и сплавы

• 
  С помощью таблицы.
  
• 
  Применение систем линейных уравнений.
  
• 
  Старинный способ
  

5. Решение задачи с помощью таблицы.

Рассмотрим решения задач с применением таблицы. Таблица для решения

задач имеет вид:(Таблица 1)

Наименование веществ, растворов, смесей, сплавов	Масса раствора (смеси, сплава)	% содержание вещества (доля содержания вещества)	Масса вещества

Табл. 1.

Данный способ является самым распространённым и лёгким.

Задача1

Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?

Решение:

Наименование веществ, растворов, смесей, сплавов	Масса раствора	%	Масса вещ-ва
1	200г	70%	200×0.7=140г
2	Х г	0%
Получившийся сплав	200+Х	8%	200×0.7=140г

Табл. 2.

Исходя из сведений найденных с помощью таблицы, решим уравнение:

0.08×(200+х)=140

16+0.08х=140

0.08х=124

Х=1550г

Ответ:1.55 кг воды

6. Применение систем линейных уравнений

Идею общего метода решения систем линейных уравнений высказал Лейбниц в 1693 году. Она была реализована швейцарским математиком Крамером в 1752 году. Он сформулировал и обосновал правило, носящее теперь его имя, которое позволяет решать системы n линейных уравнений с n неизвестными и буквенными коэффициентами.

---

1. 
   Обозначить одну неизвестную величину через х, другую неизвестную величину через у.
   
2. 
   Составить систему двух линейных уравнений по условию задачи.
   
3. 
   Решить получившуюся систему уравнений.
   
4. 
   Перейти к условию задачи (ответить на вопрос).
   
5. 
   Записать ответ
   

Задача

Смешав 25 -процентный и 95 -процентный растворы кислоты и добавив 20 кг чистой воды, получили 40 -процентный раствор кислоты. Если бы вместо 20 кг воды добавили 20 кг 30 -процентного раствора той же кислоты, то получили бы 50 -процентный раствор кислоты. Сколько килограммов 25 -процентного раствора использовали для получения смеси?

Решение

1.Обозначим массу раствора с 25 -процентным содержанием кислоты за X, а массу раствора с 95 -процентным содержанием кислоты за Y

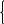
2. 0,25х + 0,95y +0*20=0,4(x+y+20) *100

0,25х + 0,95y +0,3*20=0,5(x+y+20) *100

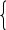
25x+ 95y+0= 40(x+y+20)
25x+ 95y+30*20= 50(x+y+20)

3. Из второго уравнения вычтем первое. Одинаковые части вычтутся и получим новую систему:

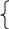25x+ 95y+0= 40(x+y+20) 5x+19y=8(x+y+20)
30*20= 10(x+y+20) y=40-x

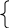
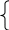y=40-x x=20

3x-11(40-x)+160=0 y=20

4. Для получения смеси потребовалось 20 килограммов 25 -процентного раствора

5. Ответ: 20 кг

7. Старинный способ

Таким способом можно решать задачи на смешивание (сплавление) любого числа веществ. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Леонтия Филипповича Магницкого ( автор первой в России учебной энциклопедии по математике).

---

Леонтий Филиппович [9.06.1669 — 19.10.1739], русский математик; педагог. По некоторым сведениям, учился в Славяно-греко-латинской академии в Москве. С 1701 до конца жизни преподавал математику в Школе математических и навигацких наук. В 1703 напечатал свою "Арифметику", которая до середины 18 века была основным учебником математики в России.

Данный способ позволяет получить правильный ответ за очень короткое время и с минимальными усилиями.

В основу метода Магницкого положено составление пропорции с помощью шаблона «Рыба». (Рис.2)



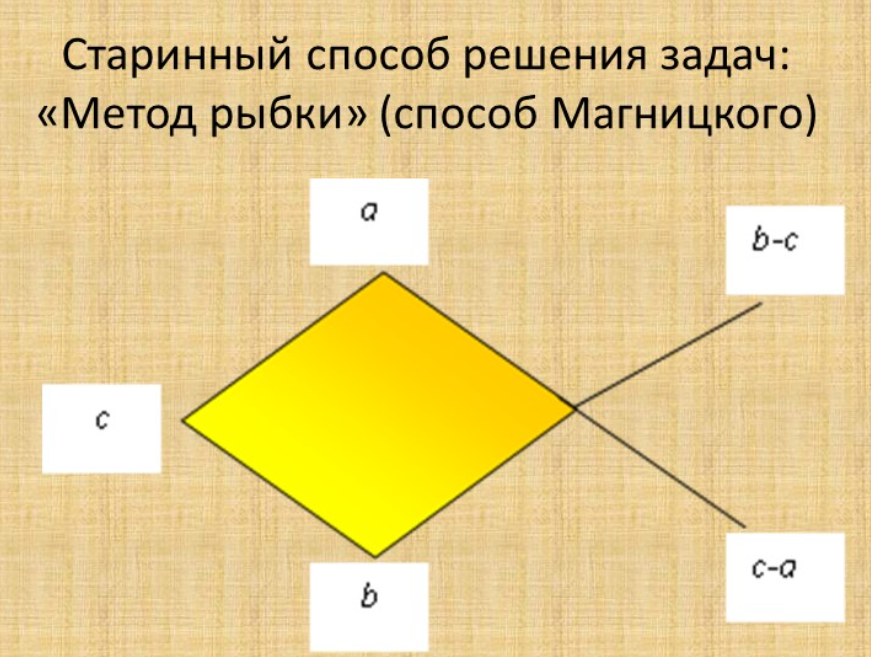
Рис.2

Задача.

Два литра шестипроцентного раствора соляной кислоты разбавили тремя литрами однопроцентного раствора этой кислоты. Каково процентное содержание кислоты в полученном растворе?

В данной задаче неизвестна концентрация конечного продукта. Эти задачи вызывают у школьников затруднения при заполнении шаблона. величина концентрации полученного раствора больше концентрации данного раствора с меньшим процентным содержанием кислоты, но меньше концентрации данного раствора с большим процентным содержанием кислоты. (Рис.3)



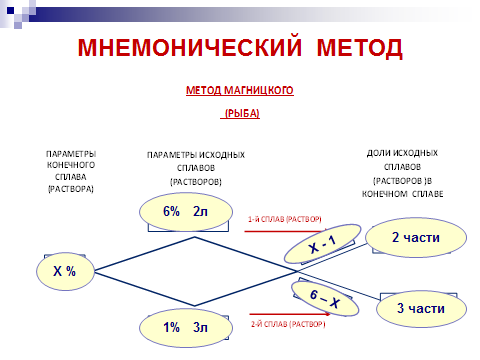
(Рис.3)

Составляем и решаем пропорцию:  .

12-2х=3х-3

5х=15

х=5

Ответ: 5%

8. Практическая часть

Мне было предложено решить несколько задач разными способами. Все задачи были взяты из сборников задач для подготовки к ЕГЭ, а также олимпиадные задачи по данной теме.

Задача №1

Если смешать 40-процентный раствор кислоты и 92-процентный раствор этой же кислоты и добавить 10 кг чистой воды, получится 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентый раствор кислоты. Сколько килограммов 40-процентного раствора использовали для получения смеси?

Решение (система линейных уравнений)

1. 
   Обозначим массу раствора с 25 -процентным содержанием кислоты за X, а массу раствора с 95 -процентным содержанием кислоты за Y
   
2. 
   0,4х + 0,9y +0*10=0,62(x+y+10) *100
   

---