Файл: Методы решения задач на смеси и сплавы.docx

0,4х + 0,9y +0,5*10=0,72(x+y+10) *100

40х+90у=62(х+у+10)

40х+90у+50*10=72(х+у+10)

3. 
   Из второго уравнения вычтем первое. Одинаковые части вычтутся и получим новую систему:
   

40х+90у+50*10=72(х+у+10) у=(40-х)

50*10=10(х+у+10) 40х+90*(40-х)+50*10=72(х+(40-х)+10)

х=10

у=30

4. 
   Для получения смеси потребовалось 10 килограммов 40 -процентного раствора.
   
5. 
   Ответ: 10 кг
   

Задача №2

Сплав меди и цинка массой 36 кг содержит 45% меди. Какую массу меди следует к нему добавить, чтобы получить сплав, содержащий 60% меди?

Решение (метод таблицы)

Наименование веществ, сплавов	Масса сплава	% содержание вещества (доля содержания вещества)	Масса вещества
1.	36 кг	45%	36*0,45=16,2 кг
2.	Х кг	0%
Получившийся раствор	36+х	60%	16,2+х

Табл.3

Исходя из сведений, найденных с помощью таблицы, составим и решим уравнение:

(36+х) *0,6=16,2+х

0,4х=5,4

х=13,5 кг

Ответ: 13,5 кг меди.

Задача №3

Первый сплав содержит 5% меди, а второй – 11% меди. Масса второго сплава больше массы первого на 4 кг из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.

Решение(метод «рыбка»)

Для начала обозначим массу первого сплава за х кг, тогда масса второго сплава х+4 кг. Составим схему и заполним все данные, которые известны по условию задачи.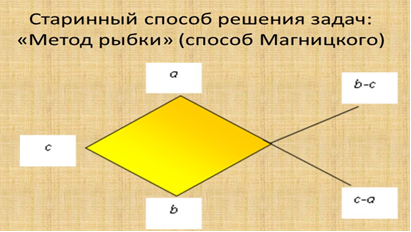

---

(Рис.4)

Составим пропорцию и решим её.

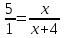
5х=х+4

х=1

Мы нашли массу первого сплава, но по условию нам нужно найти массу третьего.
Масса третьего сплава равна сумме масс первого и второго сплава, следовательно масса третьего слава равна 6 кг

Ответ: 6 кг.

9. Заключение

В ходе выполнения своей исследовательской работы я считаю, мне удалось обобщить и систематизировать изученный материал по выше указанной теме.

Способов решения задач на смеси и сплавы очень много. Я нашёл 3 самых простых и понятных способов решения этих задач. Нужно отметить, что каждый из них по-своему уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на контрольных работах и экзаменах. При работе над темой я ставил задачу выяснить, какие методы являются стандартными, а какие нестандартными.

Решая задачи на смеси и сплавы, я понял, что одни задачи можно решить разными способами, а для других некоторые способы не применимы. У каждого способа есть свои положительные стороны и недостатки.

Название способа решения задач	Положительные стороны	Недостатки
Применение систем линейных уравнений	Легко обозначить величины через две переменные	Требуются навыки по решению систем уравнений.
Старинный способ	Данный способ позволяет получить правильный ответ за очень короткое время и с минимальными усилиями.	Не каждый его понимают. Не самый лёгкий способ.
С помощью таблицы	За минимальное количество действий можно решить задачу. Задача легко понимается, благодаря наглядности.	Неправильное составление таблицы приведёт к неверному ответу. Требуется внимательность.

---

В итоге, Решение задач на растворы, смеси и сплавы являются хорошим накоплением опыта решения задач. Такой вид работы делает мышление учащихся оперативным, воспитывает творческое отношение к тем задачам, учит учащихся прогнозированию.

В задачах этого типа прослеживается системный подход к решению задач. Происходит успешная отработка и закрепление интеллектуальных умений (анализ, синтез, аналогия, обобщение. конкретизация и т.д.). 

 

Список литературы.

• 
  Математика профильный уровень. Типовые варианты экзаменационных заданий. Под редакцией И. В. Ященко. Издательство «экзамен»
  
• 
  https://yandex.ru/tutor/subject/tag/problems/?ege_number_id=48&tag_id=160
  
• 
  https://obuchonok.ru/node/1966
  
• 
  https://infourok.ru/metod-ribki-dlya-uchiteley-matematiki-3286940.html
  
• 
  https://youclever.org/book/zadachi-na-smesi-i-splavy-1/
  

---