Файл: Лабораторная работа 1. Массивы и матрицы в Scilab. Решение задач линейной алгебры 4 Теоретическая часть 4 Задание 5 Задание 6.docx

Федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича».

Факультет Институт непрерывного образования (ИНО)

Лабораторные работы №1-6

По дисциплине “Теория информации, данные, знания”

Вариант 2 (1910622)

Фамилия: Кременцов

Имя: Владимир

Отчество: Романович

Курс: 2

№ зачетной книжки: 1910622

Группа №: ИБ-94з


Санкт-Петербург

2021

Оглавление

Введение

Scilab – это пакет прикладных математических программ, предоставляющий открытое окружение для инженерных (технических) и научных расчётов. Это самая полная общедоступная альтернатива MATLAB.

Scilab содержит сотни математических функций, и есть возможность добавления новых, написанных на различных языках (C, C++, Fortran и т. д.). Также имеются разнообразные структуры данных (списки, полиномы, рациональные функции, линейные системы), интерпретатор и язык высокого уровня.

В системе доступно множество инструментов:

• 
  2D и 3D графики, анимация
  
• 
  Линейная алгебра, разреженные матрицы (sparse matrices)
  
• 
  Полиномиальные и рациональные функции
  
• 
  Интерполяция, аппроксимация
  
• 
  Симуляция: решение ОДУ и ДУ
  
• 
  Scicos: гибрид системы моделирования динамических систем и симуляции
  
• 
  Дифференциальные и не дифференциальные оптимизации
  
• 
  Обработка сигналов
  
• 
  Параллельная работа
  
• 
  Статистика
  
• 
  Работа с компьютерной алгеброй
  
• 
  Интерфейс к Fortran, Tcl/Tk, C, C++, Java, LabVIEW
  

---

Лабораторная работа №1. «Массивы и матрицы в Scilab. Решение задач линейной алгебры»

Теоретическая часть

Для работы с множеством данных удобно использовать массивы. Например, можно создать массив для хранения числовых или символьных данных. В этом случае вместо создания переменной для хранения каждого данного достаточно создать один массив, где каждому элементу будет присвоен порядковый номер. Таким образом, массив — множественный тип данных, состоящий из фиксированного числа элементов.

Как и любой другой переменной, массиву должно быть присвоено имя. Переменную, представляющую собой просто список данных, называют одномерным массивом, или вектором. Для доступа к данным, хранящимся в определенном элементе массива, необходимо указать имя массива и порядковый номер этого элемента, называемый индексом.

Если возникает необходимость хранения данных в виде таблиц, в формате строк и столбцов, то необходимо использовать двумерные массивы (матрицы). Для доступа к данным, хранящимся в таком массиве, необходимо указать имя массива и два индекса: первый должен соответствовать номеру строки, а второй — номеру столбца, в которых хранится необходимый элемент. Значение нижней границы индексации в Scilab равно единице. Индексы могут быть только целыми положительными числами.

Задание 1.1.

Решить систему линейных алгебраических уравнений, сделать проверку.



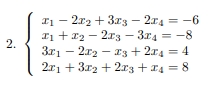
Решение:



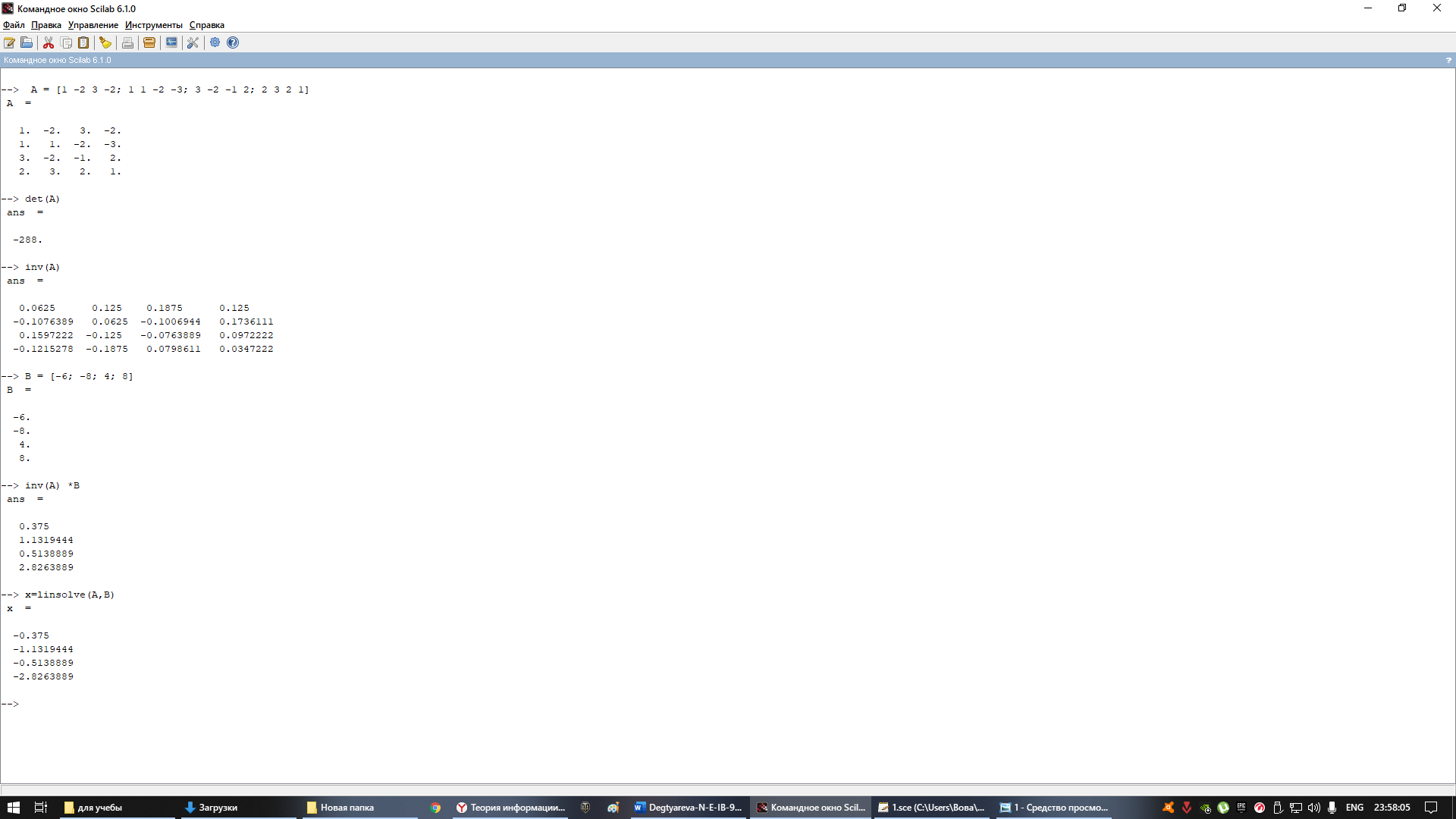
Обьяснение:

Для начала нам нужно задать матрицу А в scilab, после чего вычисляем определитель и обратную матрицу, затем задаем матрицу В в Scilab, умножаем матрицы А и В и в конце проверяем все с помощью команды linsolve.

Задание 1.2.

Если возможно, вычислить матрицу, обратную к матрице D



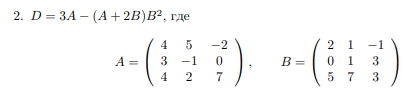
Решение:



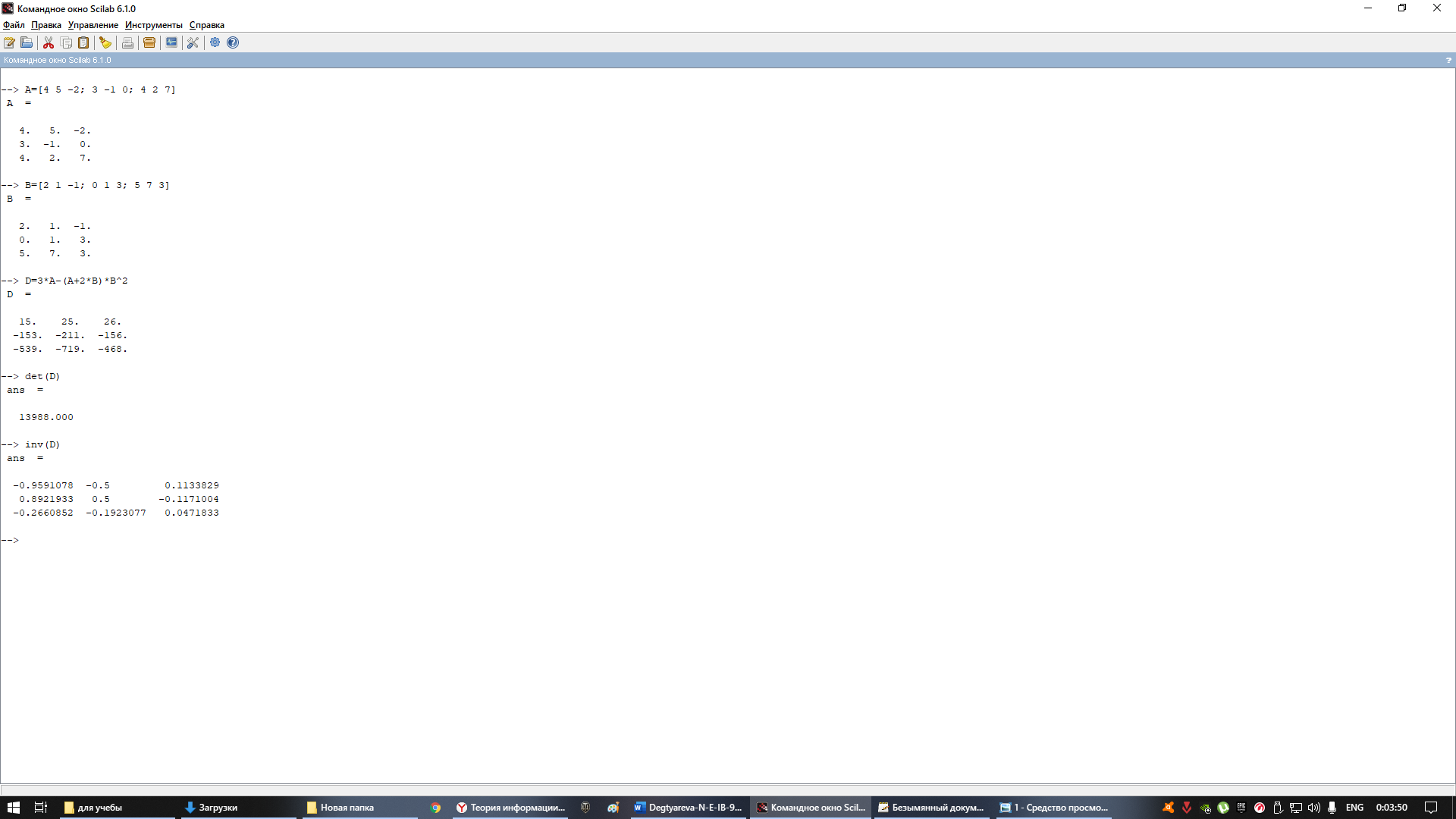
Обьяснение:

Для начала мы задали матрицы А и В в scilab, после чего вычислили матрицу D, ее определитель и в конце концов обратную матрицу к D.

---

Вывод

В лабораторной работе №1 посвященной массивам и матрицам в Scilab, а также решению задач линейной алгебры мы научились решать системы линейных алгебраических уравнений и делать их проверку; вычислять обратные матрицы.

Лабораторная работа №2. «Построение двумерных графиков»

Теоретическая часть

В этой лабораторной работе мы применим графический аппарат Scilab для построения двумерных графиков. Двумерными будем считать такие графики, в которых положение каждой точки задается двумя величинами.

Рассмотрение графиков начнем с простейших функций вида y = f(x), для построения которых в Scilab существует функция plot. В предыдущих версиях Scilab (по третью версию Scilab включительно) функция plot предназначена для построения графика одной функции y = f(x). Обращение к ней имеет вид:

plot(x,y,[xcap,ycap,caption])

Здесь x — массив абсцисс; y — массив ординат; xcap, ycap, caption — подписи осей X, Y и графика соответственно.

При простейшем обращении к функции plot(x,y) создается окно с именем Scilab Graphic (0), в котором будет построен график функции y(x) на заданном интервале. Если же повторно обратиться к функции plot, будет создано новое графическое окно, и в нем будет построен новый график.

Задание 2.1.

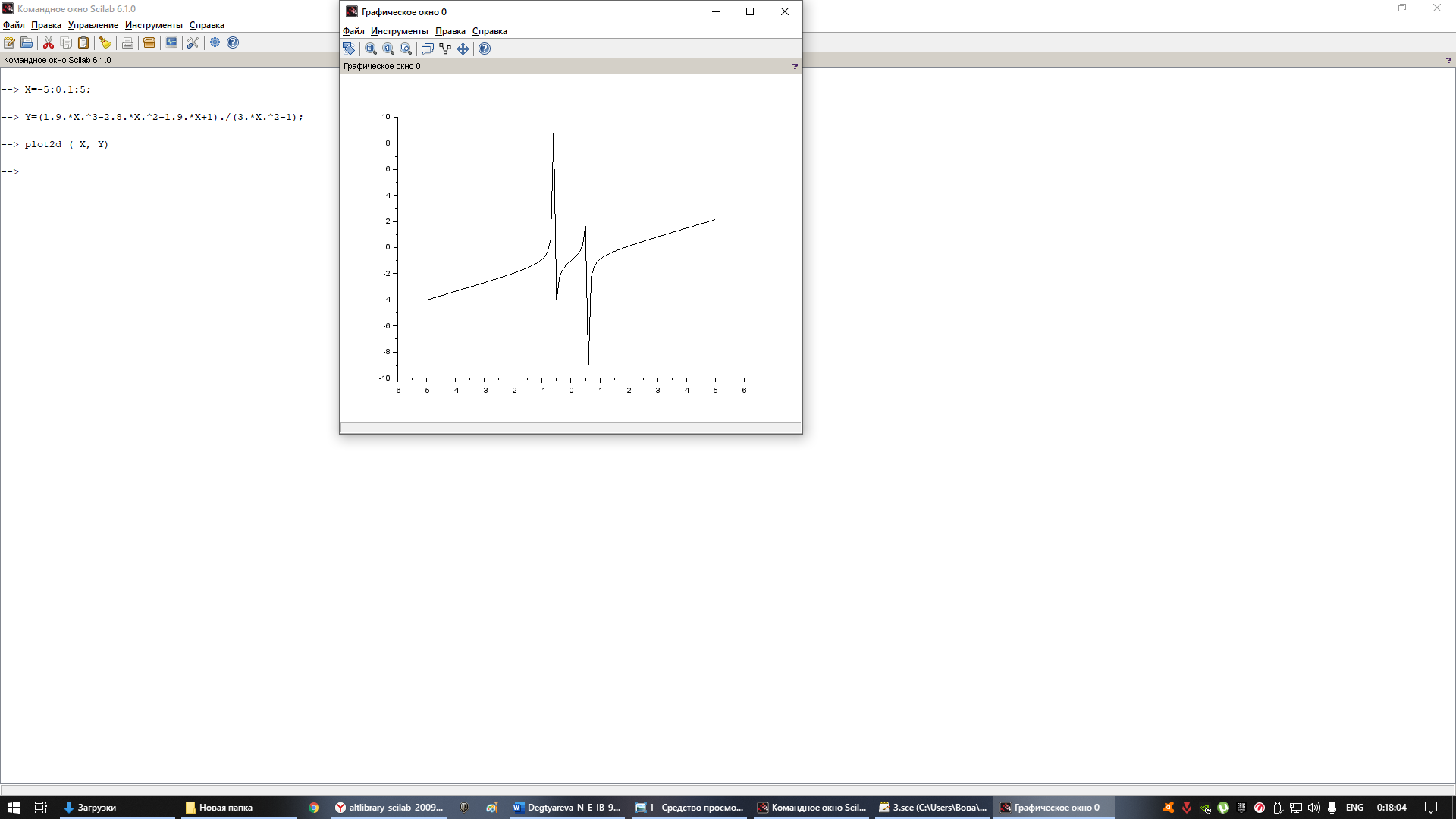
Изобразите график функции f(x).



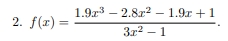
Решение:



Обьяснение:

Для начала мы задали две переменные X и Y в scilab, выполнили функцию plot2d и получили график.

Задание 2.2.

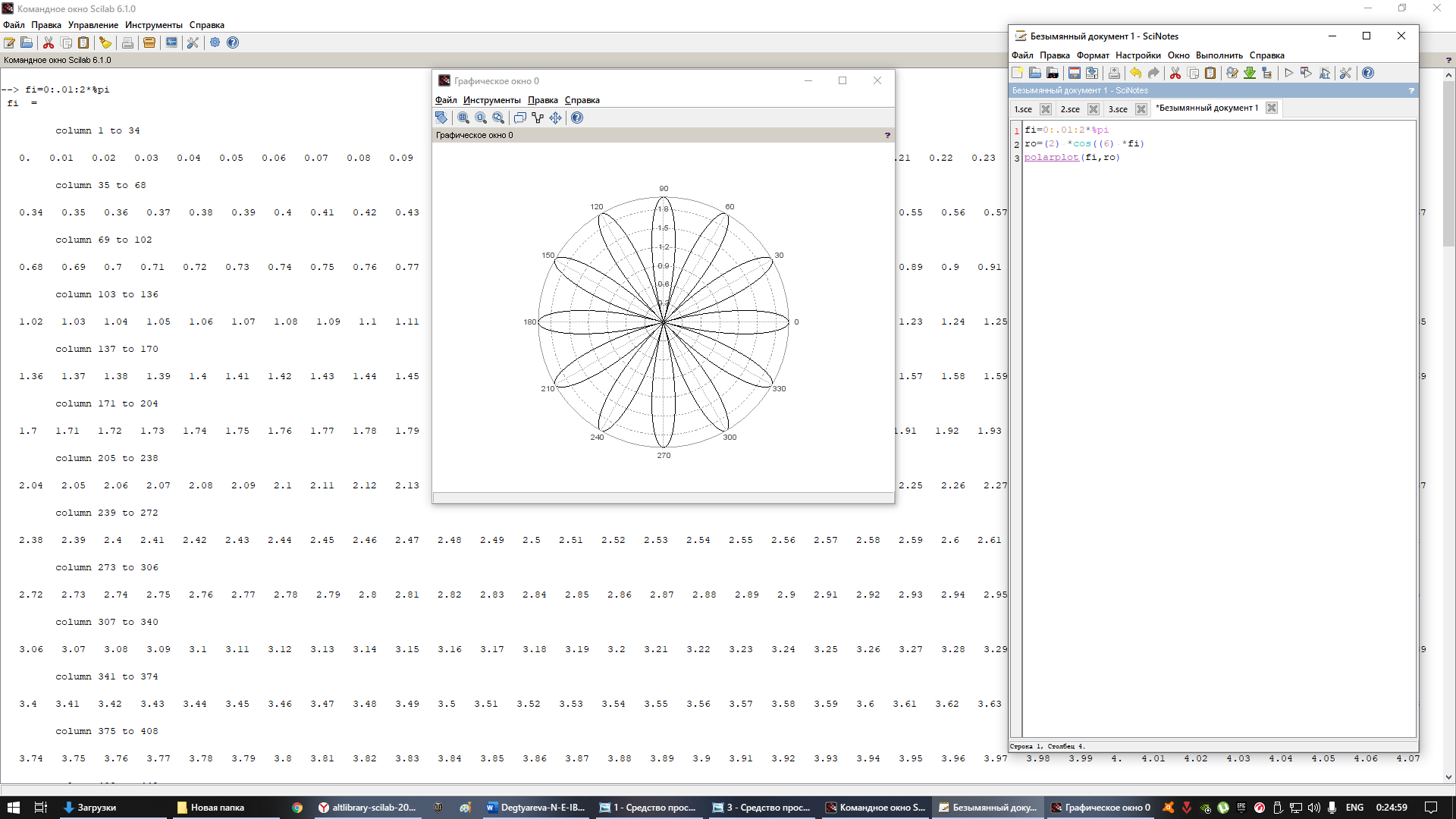
Изобразите график функции в полярных координатах



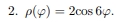
Решение:



Обьяснение:

Для начала мы задали параметры функции, после чего выполнили функцию polarplot и получили график.

Вывод

В лабораторной работе №2 посвященной построению двумерных графиков мы научились изображать двумерные графики и графики в полярных координатах.

Лабораторная работа №3. «Построение трехмерных графиков»

---

В данной лабораторной работе будут рассмотрены основные возможности Scilab по созданию трехмерных графиков — объемных и пространственных. При этом к трехмерным отнесем все графики, положение каждой точки которых задается тремя величинами.

В Scilab поверхность можно построить с помощью функций plot3d или plot3d1. Их отличие состоит в том, что plot3d строит поверхность и заливает ее одним цветом, а plot3d1 — поверхность, каждая ячейка которой имеет цвет, зависящий от значения функции в каждом соответствующем узле сетки.

Задание 3.1.

Построить график, заданный системой уравнений





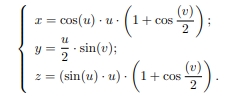
Решение:



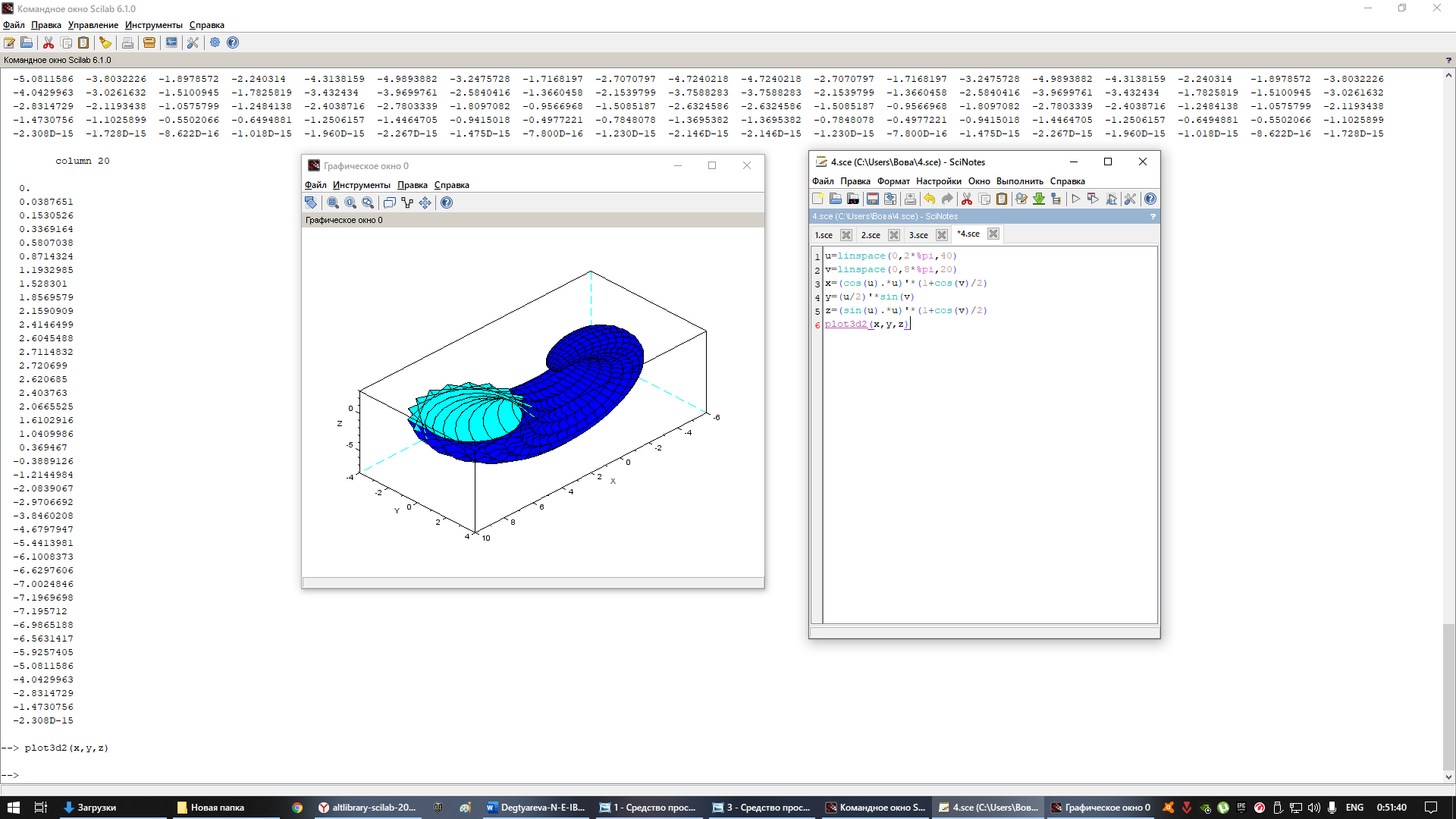
Обьяснение:

Для начала мы задали массивы значений для параметров u и v, после чего вычислили значения функций и выполнили функцию plot3d2 с помощью которой получили график.

Задание 3.2.

Изобразить линии, заданные параметрически

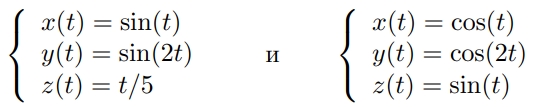
Решение:



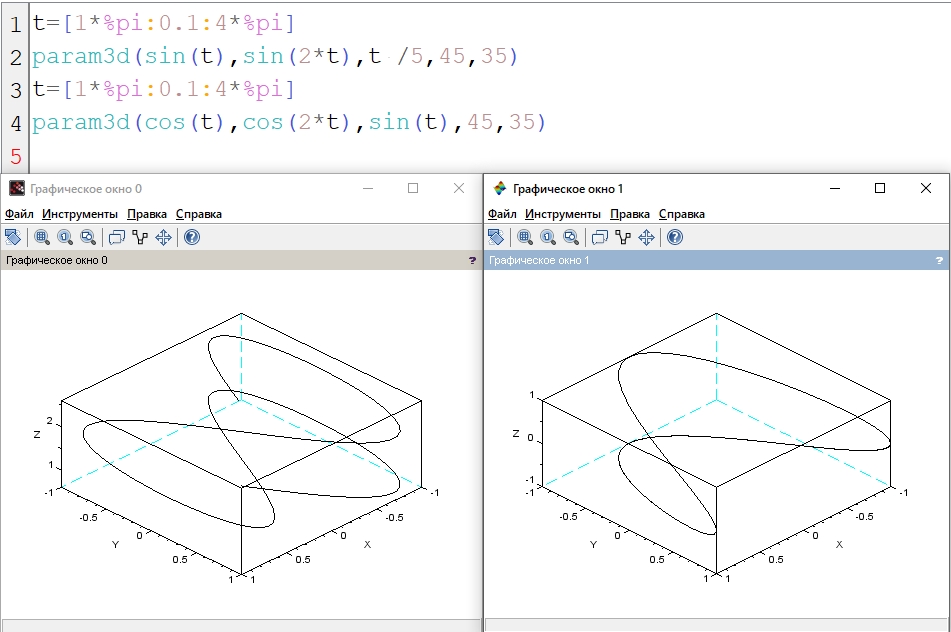
Обьяснение:

Для начала мы задали параметры наших графиков, после чего прописали функцию param3d и построили с ее помощью график

Вывод

В лабораторной работе № 3 посвященной построению трехмерных графиков мы научились строить график, заданный системой уравнений и изображать параметрические линии.

Лабораторная работа №4. «Нелинейные уравнения и системы»

Теоретическая часть

Любое уравнение P(x) = 0, где P(x) — это многочлен, отличный от нулевого, называется алгебраическим уравнением или полиномом. Всякое алгебраическое уравнение относительно x можно записать в виде

a0x n+a1xn−1+· · ·+an−1x+an = 0, где a0 6= 0, n > 1 и ai — коэффициенты алгебраического уравнения n–й степени.

Например, линейное уравнение — это алгебраическое уравнение первой степени, квадратное — второй, кубическое — третьей и так далее.

---

Решение алгебраического уравнения в Scilab состоит из двух этапов. Необходимо задать полином P(x) с помощью функции poly, а затем найти его корни, применив функцию roots.

Итак, определение полиномов в Scilab осуществляет функция

poly(a, "x ["fl"]),

где a — это число или матрица чисел, x — символьная переменная, fl — необязательная символьная переменная, определяющая способ задания полинома. Символьная переменная fl может принимать только два значения — «roots» или «coeff» (соответственно «r» или «c»). Если fl=c, то будет сформирован полином с коэффициентами, хранящимися в параметре a. Если же fl=r, то значения параметра a воспринимаются функцией как корни, для которых необходимо рассчитать коэффициенты соответствующего полинома. По умолчанию fl=r.

Следующий пример отражает создание полинома p, имеющего в качестве корня тройку, и полинома f с коэффициентом 3.

Задание 4.1.

Найти корни полиномов.



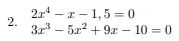
Решение:



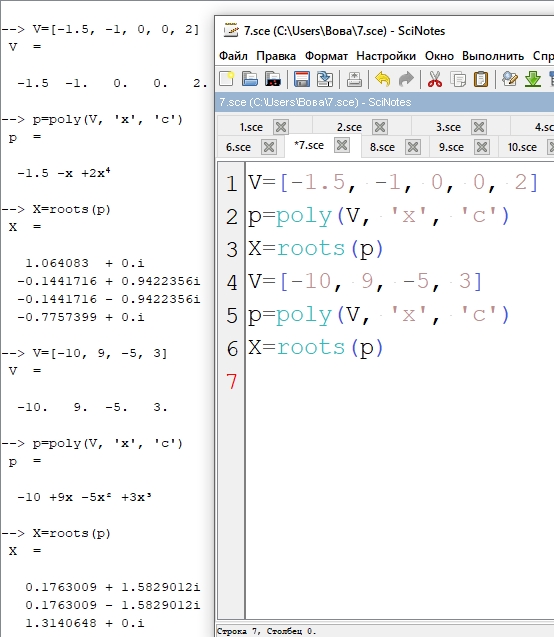
Обьяснение:

Для начала мы задали полиномы, после чего находим их корни.

Задание 4.2.

Решение решить систему уравнений



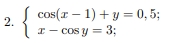
Решение:



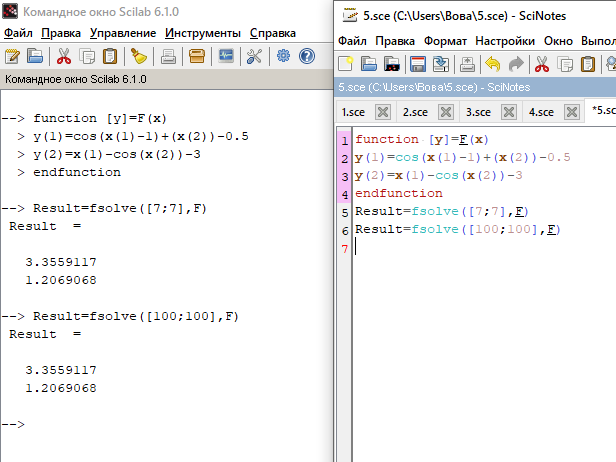
Обьяснение:

Для начала мы задали пользовательскую функцию, после чего с помощью fsolve получаем ответ.

Вывод

В лабораторной работе № 4 посвященной нелинейным уравнениям и системам мы научились находить корни полиномов и решать системы уравнений.

Лабораторная работа №5. «Обработка экспериментальных данных»

Теоретическая часть

Метод наименьших квадратов позволяет по экспериментальным данным подобрать такую аналитическую функцию, которая проходит настолько близко к экспериментальным точкам, насколько это возможно.

Пусть в результате эксперимента были получены некоторые данные, отображенные в виде таблицы (табл. 11.1). Требуется построить аналитическую зависимость, наиболее точно описывающую результаты эксперимента

---