Файл: Лабораторная работа 1. Массивы и матрицы в Scilab. Решение задач линейной алгебры 4 Теоретическая часть 4 Задание 5 Задание 6.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 115
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Лабораторная работа №1. «Массивы и матрицы в Scilab. Решение задач линейной алгебры»
Лабораторная работа №2. «Построение двумерных графиков»
Лабораторная работа №3. «Построение трехмерных графиков»
Изобразить линии, заданные параметрически
Лабораторная работа №4. «Нелинейные уравнения и системы»
Лабораторная работа №5. «Обработка экспериментальных данных»

Идея метода наименьших квадратов заключается в том, что функцию Y = f(x, a0, a1, . . . , ak) необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений yi от расчетных Yi была наименьшей:
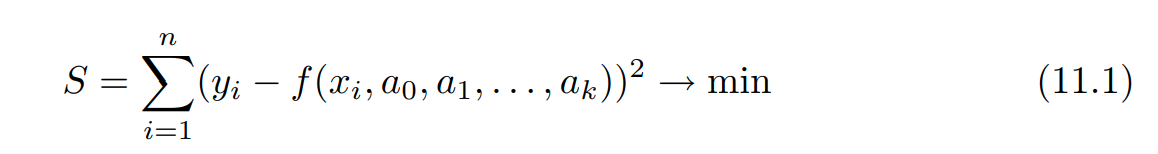 Задача сводится к определению коэффициентов ai из условия (11.1). Для реализации этой задачи в Scilab предусмотрена функция
Задача сводится к определению коэффициентов ai из условия (11.1). Для реализации этой задачи в Scilab предусмотрена функция[a,S]=datafit(F,z,с)
Задание 5.1.
В результате эксперимента была определена некоторая табличная зависимость. С помощью метода наименьших квадратов определить линию регрессии, рассчитать коэффициент корреляции, подобрать функциональную зависимость заданного вида, вычислить коэффициент регрессии. Определить суммарную ошибку.

Решение:
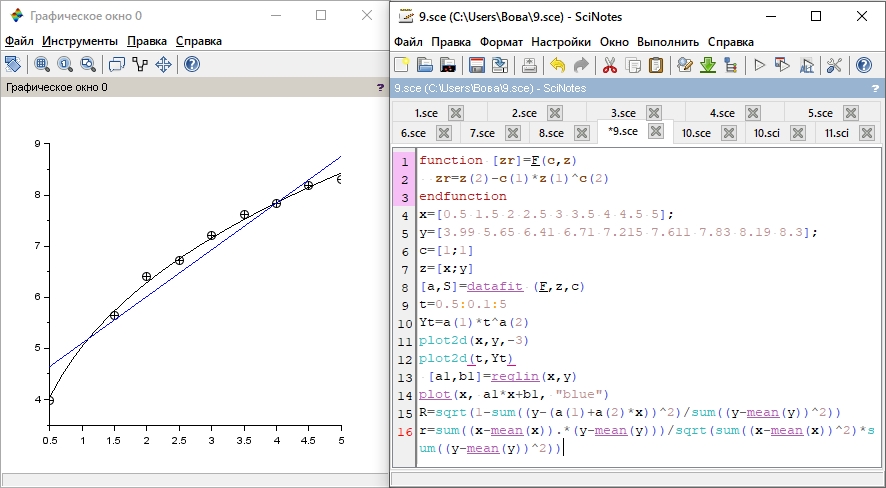
Обьяснение:
Для начала мы задали пользовательскую функцию и массивы экспериментальных данных, сформировали матрицу исходных данных, нашли вектора коэффициентов и суммарную ошибку, построили графики экспериментальных данных и функциональной зависимости, нашли коэффициенты регрессии и добавили линию регрессии на график и наконец нашли коэффициент корреляции r и индекс корреляции R.
Задание 5.2.
Для вариантов 1-7 найти приближенное значение функции при заданном значении аргумента с помощью функции линейной интерполяции. Функция задана таблично.

Решение:
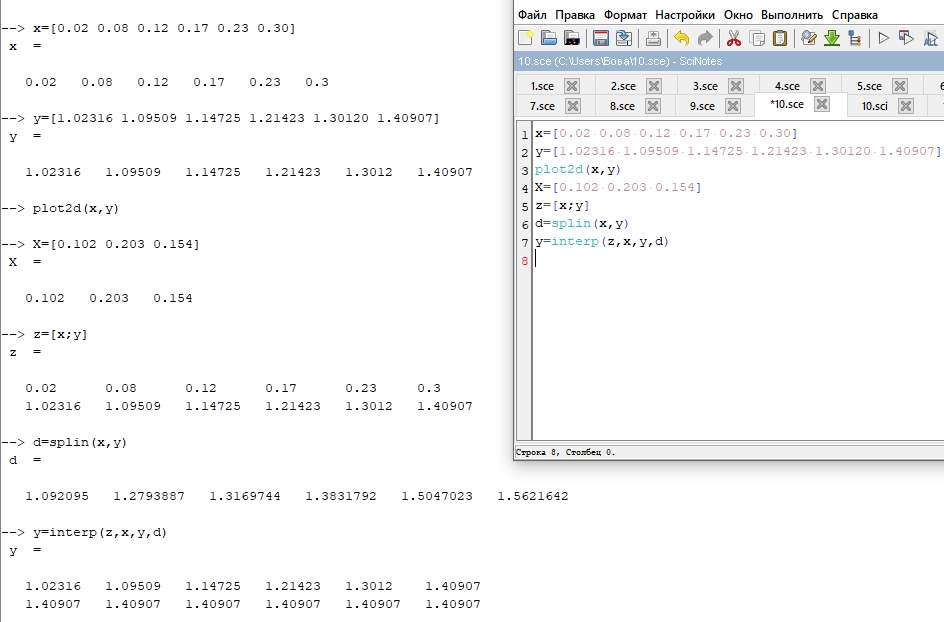
Обьяснение:
Для начала мы задали массивы значений, создали график регрессии задали массив значения х в заданных точках, создали матрицу исходных данных и сплайн-интерполяцию.
Вывод
В лабораторной работе №5 посвященной обработке экспериментальных данных мы научились с помощью метода наименьших квадратов определять линию регрессии, рассчитывать коэффициент корреляции, подобирать функциональную зависимость заданного вида, вычислять коэффициент регрессии и определять суммарную ошибку, а также искать приближенное значение функции при заданном значении аргумента с помощью функции линейной интерполяции.
Лабораторная работа №6. «Решение задач оптимизации»
Теоретическая часть
При нахождении минимума функции многих переменных функцию costf необходимо построить таким образом, чтобы входными данными в нее были значения вектора неизвестных x и параметра ind. Функция costf должна зависеть не от нескольких неизвестных, а от одного массива (вектора) неизвестных. В случае функции многих переменных структура функции сostf должна быть такой:

Задание 6.
Решить задачу целочисленного программирования.
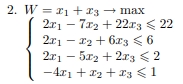
Решение:
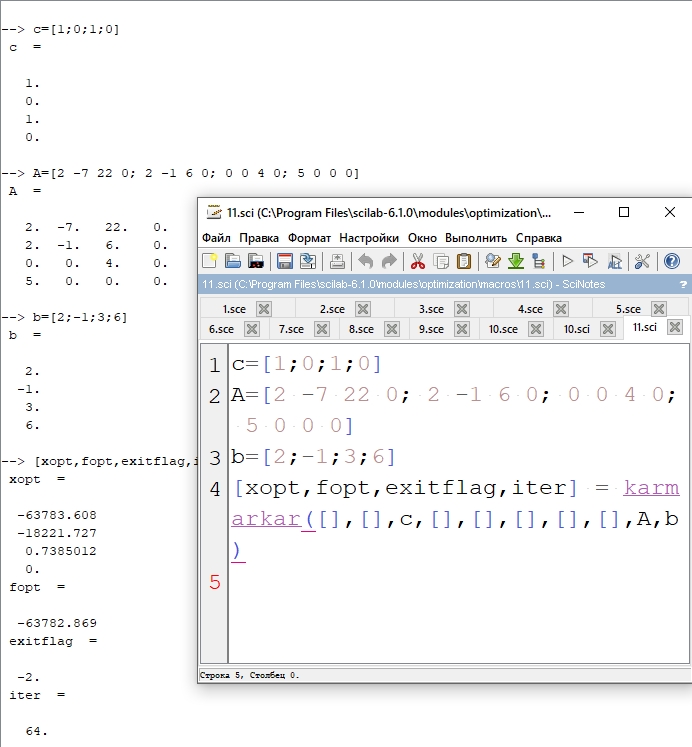
Обьяснение:
Для начала мы задали массив коэффициентов функции цели, матрицу при неизвестных левой части неравенства и массив, который содержит свободные члены системы ограничений, после чего применили функцию karmarkar.
Вывод
В данной лабÐ