Файл: Лабораторная работа 4 Краткое описание Понятие цикла Виды циклов.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.12.2023

Просмотров: 45

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Лабораторная работа № 4

do

do

Самостоятельная работа

....

Написать отчет по лабораторной работ

Лабораторная работа № 4


Краткое описание:

Понятие цикла Виды циклов

Запустить Microsoft Visual Studio, выбрав приложение Microsoft Visual C#

Начать новый проект – Консольное приложение

Цикл – многократное повторение однотипных действий, со- бытий или состояний.

Циклы могут повторяться фиксированное число раз, или за- вершаться при выполнении определенного условия.

  1. Циклы с предусловием


Цикл с предусловием — цикл, который выполняется пока истинно некоторое условие, указанное перед его началом. Это условие проверяется до выполнения тела цикла, поэтому тело может быть не выполнено ни разу (если условие с само- го начала ложно). В большинстве процедурных языков про- граммирования реализуется оператором while, отсюда его второе название — while-цикл.
while (Условие)

{
Тело цикла
}

while (x<0)

{

y*=4;

z += 10;

x += 10;

  1. Циклы с постусловием


Цикл с постусловием — цикл, в котором условие про- веряется после выполнения тела цикла. Отсюда следу- ет, что тело всегда выполняется хотя бы один раз.

do


{

Тело цикла
} while (Условие);

do {

y *= 4;

z += 10;

x += 10;

} while (x < 0);


  1. Циклы со счетчиком



Цикл со счётчиком — цикл, в котором некото- рая переменная изменяет своё значение от заданного начального значения до конечного значения с некото- рым шагом, и для каждого значения этой переменной тело цикла выполняется один раз. В большинстве про- цедурных языков программирования реализуется опе- ратором for, в котором указывается счётчик (так назы- ваемая «переменная цикла»), требуемое количество проходов (или граничное значение счётчика) и, воз- можно, шаг, с которым изменяется счётчик.

for(начальное значение; условие; прира- щение)

{

Тело цикла

for (int i = 25; i < 125; i+=5)

{

s = s + i;

skv = skv + Math.Pow(i, 2);

}


  1. Вложенные циклы


Существует возможность организовать цикл внутри тела другого цикла. Такой цикл будет называть- ся вложенным циклом. Вложенный цикл по отноше- нию к циклу в тело которого он вложен будет имено- ваться внутренним циклом, и наоборот цикл в теле ко- торого существует вложенный цикл будет именовать- ся внешним по отношению к вложенному. Внутри вложенного цикла в свою очередь может быть вложен еще один цикл, образуя следующий уровень вложенно- сти и так далее. Количество уровней вложенности, как правило, не
ограничивается.
Задание 6. Пример программы, в которой использова- ны все циклы.

Создать новый проект, набрать код программы, запус- тить программу на выполнение, используя разные ва- рианты входных данных.

using System;

using System.Collections.Generic; using System.Linq;

using System.Text;
namespace ConsoleApplication1

{

class Program

{

static void Main(string[] args)

{

int x, z, f; double y,k,s, skv;

//Посчитать факториал числа n

Console.WriteLine("Введите число для определения факториала");

Int n=Convert.ToInt32 (Console.ReadLine());

f = 1;

x = 1;

while (x<=n)

{

f=f*x; x +=1;

}

Console.WriteLine("Факторил числа

{0} равен {1}",n,f); Console.ReadLine();
//Сумма кубов четных чисел меньших половины заданного z

Console.WriteLine("Введите z");

z = Convert.ToInt32(Console.ReadLine());

k = 2;

s = 0;

int b = 0;

do


{

if (k%2==0) {

y = Math.Pow(k,3); s=s+y;

b += 1;

}

k += 1;

} while (k < z/2);
Console.WriteLine("Сумма кубов пер- вых {0} четных чисел меньших {1} равна

{2}", b, z/2, s);

Console.ReadLine();

//Cумма чисел от 25 до 125 кратных 5, и сумма квадратов этих чисел

s = 0;

skv = 0;

for (int i = 25; i < 125; i+=5)

{

s = s + i;

skv = skv + Math.Pow(i, 2);

}

Console.WriteLine("Сумма чисел от

25 до 125 кратных 5 равна {0}, \nсумма квадратов равна {1}", s, skv);

Console.ReadLine();
/*Даны натуральные числа n, m. Получить все меньшие n натуральные числа, сумма цифр которых равен m. */

Console.WriteLine("Введите n"); n=Convert.ToInt32(Console.ReadLine());

Console.WriteLine("Введите m");

int m=Convert.ToInt32(Console.ReadLine());

int u, v;
for (int i = 0; i < n; i++) { s = 0;

u=i;

while (u>0)

{

v=u%10;

s=s+v;

u = u / 10;

}

if(s==m) Console.WriteLine("Число

{0}, сумма цифр равна {1}",i, m);

}
Console.ReadLine();

}

}

}




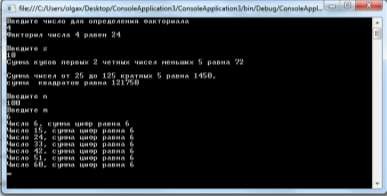
Рисунок 3. Вариант вывода результата на Консоль


Самостоятельная работа



Циклы с предусловием


  1. Найти сумму цифр числа.

  2. Приписать по 1 в начало и в конец записи числа n. Например, было n=3456, стало n=134561.

  3. Поменять местами первую и последнюю цифры числа.

  4. Поменять порядок цифр числа на обратный. На- пример, было 12345, стало 54321.

  5. Найти количество чётных цифр целого положи- тельного числа.

  6. Найти самую большую цифру целого числа.

  7. Найти сумму цифр целого числа, больших 5.

  8. Сколько раз данная цифра встречается в целом числе?

  9. Составить программу, проверяющую, является ли последовательность из 10 целых чисел, вводимых с клавиатуры, возрастающей.

  10. Составить программу, проверяющую, является ли заданное натуральное число палиндромом, то есть

таким, десятичная запись которого читается оди- наково слева направо и справа налево.
Циклы с постусловием


  1. Произведение максимального количества N пер- вых нечетных чисел не больше p. Вывести послед- ний сомножитель , общее количество сомножите- лей и произведение.

  2. Числа Фибоначчи (fn) определяется формулами: f0

= f1 = 1; fn = fn = fn-1 + fn-2 при n=2, 3,... Составить программу определения f - 40-е число Фибоначчи.

  1. Числа Фибоначчи (fn) определяется формулами: f0

= f1 = 1; fn = fn = fn-1 + fn-2 при n=2, 3,... Составить программу поиска f - первого числа Фибоначчи, большего m (m>1).

  1. Числа Фибоначчи (fn) определяется формулами: f0

= f1 = 1; fn = fn = fn-1 + fn-2 при n=2, 3,... Составить программу вычисления s - суммы всех чисел Фи- боначчи, которые не превосходят 1000

  1. Составить программу, проверяющую, является ли заданное натуральное число совершенным, то есть равным сумме своих положительных делителей, кроме самого этого числа.

  2. Дана непустая последовательность натуральных чисел, за которой следует 0. Вычислить сумму по- ложительных элементов последовательности, по- рядковые номера которых нечетны.

  3. Составить программу, проверяющую, является ли заданное натуральное число палиндромом, то есть таким, десятичная запись которого читается оди- наково слева направо и справа налево.

  4. Найти количество нечётных цифр целого положи- тельного числа.

  5. Найти первую цифру числа.

  6. Подсчитать сумму квадратов первых нечетных чи- сел меньших заданного Z.

Циклы со счетчиком


  1. Составить программу возведения натурального числа в квадрат, используя следующую законо- мерность:

12 = 1

22 = 1 + 3

32 = 1 + 3 + 5

42 = 1 + 3 + 5 + 7

....


n2 = 1 + 3 + 5 + 7 + 9 + ... + 2n-1

  1. Определить количество трехзначных натуральных чисел, сумма цифр которых равна заданному числу N.

  2. Составить программу вычисления суммы кубов чисел от 25 до 125.

  3. Среди двузначных чисел найти те, сумма квадра- тов цифр которых делится на 13. Ответ: .

  4. Написать программу поиска двузначных чисел, та- ких, что если к сумме цифр этого числа прибавить квадрат этой суммы, то получится это число.

  5. Квадрат трехзначного числа оканчивается тремя цифрами, которые как раз и составляют это число.

  6. Написать программу поиска четырехзначного чис- ла, которое при делении на 133 дает в остатке 125, а при делении на 134 дает в остатке 111. Ответ: 1987.

  7. Найти сумму положительных нечетных чисел, меньших 100.

  8. Найти сумму целых положительных чисел из про- межутка от A до B, кратных 4 (значения перемен- ных A и B вводятся с клавиатуры).

  9. Найти сумму целых положительных чисел, боль- ших 20, меньших 100, кратных 3 и заканчиваю- щихся на 2, 4 или 8.

Вложенные циклы

  1. Исходное данное - натуральное число q, выра- жающее площадь. Написать программу для нахо- ждения всех таких прямоугольников, площадь ко-

торых равна q и стороны выражены натуральными числами.

  1. Составить программу для графического изображе- ния делимости чисел от 1 до n (n - исходное дан- ное). В каждой строке надо печатать число и сколько плюсов, сколько делителей у этого числа. Например, если исходное данное - число 4, то на экране должно быть напечатано:

1+

2++

3++

4+++

  1. Составить программу получения всех совершен- ных чисел, меньших заданного числа n. Число на- зывается совершенным, если равно сумме всех своих положительных делителей, кроме самого этого числа. Например, 28 - совершенно, так как 28=1+2+4+7+14.

  2. Из истории. Грекам были известны первые четыре совершенных числа: 6, 28, 496, 8128. Эти числа высоко ценились. Даже в XII веке церковь утвер- ждала, что для спасения души необходимо найти пятое совершенное число. Это число было найдено только в XV веке. До сих пор совершенные числа полностью не исследованы - не известно, имеется ли конечное число совершенных чисел или их число бесконечно, кроме того, неизвестно ни од- ного нечётного совершенного числа, но и не дока- зано, что таких чисел нет.

  3. Дано натуральное число n. Можно его представить в виде суммы трёх квадратов натуральных чисел? Если можно, то:

    1. указать тройку x, y, z, таких натуральных чисел, что x2 + y2 + z2 = n;

    2. указать все тройки x, y, z таких натуральных чисел, что x2 + y2 + z2 = n.

  4. Найти натуральное число от 1 до 10000 с макси- мальной суммой делителей.

  5. Даны натуральные числа a, b (ap, удовлетворяющие неравенствам: a<=p<=b.

  6. Даны натуральные числа n, m. Получить все меньшие n натуральные числа, квадрат суммы цифр которых равен m.

  7. Даны натуральные числа n и m. Найти все пары дружественных чисел, лежащих в диапазоне от n до m. Два числа называются дружественными, если каждое из них равно сумме всех делителей другого (само число в качестве делителя не рас- сматривается).

  8. В данном натуральном числе переставить цифры таким образом, чтобы образовалось наименьшее число, записанное этими же цифрами.

  9. Составить программу, печатающую для данного натурального числа k-ю цифру последовательно- сти:

    1. 12345678910..., в которой выписаны подряд все натуральные числа;

    2. 14916253649..., в которой выписаны подряд квад- раты всех натуральных чисел;

    3. 1123581321..., в которой выписаны подряд все числа Фибоначчи.

  10. Составить программу возведения заданного числа в третью степень, используя следующую законо- мерность:

13 = 1

23 = 3 + 5

33 = 7 + 9 + 11

43 = 13 + 15 + 17 + 19

53 = 21 + 23 + 25 + 27 + 29

  1. Составить программу для нахождения всех нату- ральных решений уравнения n2 + m2 = k2 в интер- вале [1, 10].

Примечание. Решения, которые получаются пере- становкой n и m, считать совпадающими.

Написать отчет по лабораторной работ



}


Смотрите также файлы