Файл: Научная работа включает 33 страниц, 18 иллюстраций и 3 использованных литературных источников.doc

1.4. Концентрация электронов и дырок в собственном полупроводнике

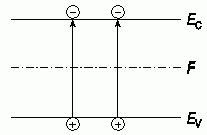
Напомним, что полупроводник называется собственным, если в нем отсутствуют донорные и акцепторные примеси. В этом случае электроны появляются в зоне проводимости только за счет теплового заброса из валентной зоны, тогда n = p (рис. 1.5).

Рис. 1.5. Заброс из валентной зоны

При отсутствии внешних воздействий (освещение, электрическое поле и т.д.) будем обозначать концентрации свободных электронов и дырок с индексом нуль, то есть n₀ и p₀ соответственно. При n₀ = p₀ из (1.14) получаем:

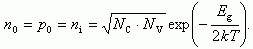   (1.15)

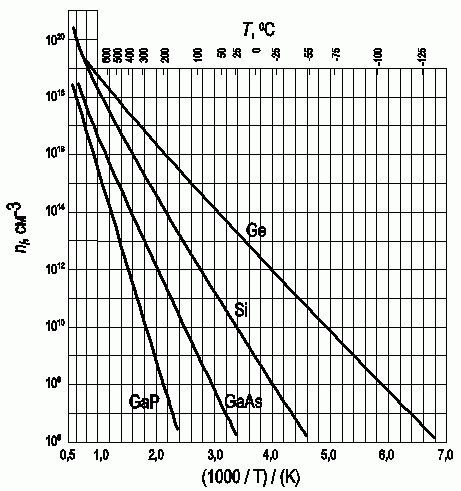
Напомним, что значком n_i принято обозначать концентрацию собственных носителей заряда в зоне проводимости и в валентной зоне. Для расчета N_C и N_V используется формула (1.11). Как следует из соотношения (1.15), концентрация собственных носителей определяется в основном температурой и шириной запрещенной зоны полупроводника. На рисунке 1.6 представлена зависимость концентрации собственных носителей от температуры для наиболее распространенных полупроводников - кремния, германия, арсенида и фосфида галлия. Видно, что при изменении ширины запрещенной зоны в диапазоне от 0,6 эВ для германия до 2,8 эВ для фосфида галлия собственная концентрация ni при комнатной температуре изменяется от значения 10¹³ см^-3 до 10¹ см^-3.

Рис. 1.6. Зависимость концентрации собственных носителей от температуры для наиболее распространенных полупроводников - кремния, германия, арсенида и фосфида галлия

1.4. Концентрация электронов и дырок в примесном полупроводнике

Уравнение (1.14) справедливо только для равновесных носителей заряда, то есть в отсутствие внешних воздействий. В наших обозначениях

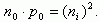   (1.16)

---

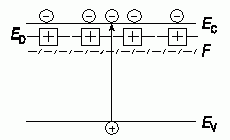
Пусть полупроводник легирован донорами с концентрацией N_D. При комнатной температуре в большинстве полупроводников все доноры ионизованы, так как энергии активации доноров составляют всего несколько сотых электронвольта. Тогда для донорного полупроводника

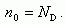   (1.17)

Рис. 1.7. Зонная диаграмма полупроводника n-типа

Концентрацию дырок в донорном полупроводнике найдем из (1.16):

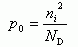   (1.18)

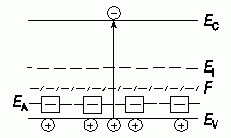
Соответственно если полупроводник легирован акцепторами с концентрацией N_A, то

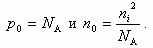   (1.19)

Рис. 1.8. Зонная диаграмма полупроводника p-типа

1.5. Определение положения уровня Ферми

В предыдущих рассуждениях мы считали, что уровень Ферми задан. Посмотрим теперь, как можно найти положение уровня Ферми.

Для собственного полупроводника уравнение электронейтральности приобретает вид p - n = 0 или p = n. Если ширина запрещенной зоны полупроводника достаточно велика (E_g много больше kT) и если эффективные массы электронов m_n и дырок m_p одного порядка, то уровень Ферми будет достаточно удален от краев зон (E_C - F > 2kT и F - E_V > 2kT) и полупроводник будет невырожденным.

Подставляя (1.10) и (1.13) в уравнение p + p_D - n - n_A = 0, имеем:

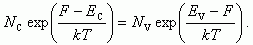   (1.20)

Отсюда вычисляем F. Уравнение (1.20) - это уравнение первого порядка относительно exp(F/kT).

Это дает

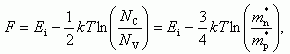   (1.21)

где через E_i = (1/2)*(E_V + E_C) обозначена энергия середины запрещенной зоны. При выводе правого выражения для F величина (N_C/N_V) была заменена на (m_n/m_p) с помощью уравнения (1.11).

Для случая m_n^* = m_p^* энергия Ферми в собственном полупроводнике находится посреди запрещенной зоны F = (E_C + E_V)/2.

Положение уровня Ферми зависит от того

---

, какие другие величины заданы. Если известны концентрации носителей заряда в зонах n и p, то значение F можно определить из формул (1.10) и (1.13). Так, для невырожденного полупроводника n-типа имеем:

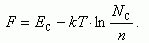   (1.22)

Аналогично для невырожденного полупроводника p-типа

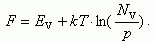   (1.23)

Из выражений (1.22 и 1.23) видно, что чем больше концентрация основных носителей, тем ближе уровень Ферми к краю соответствующей зоны. Для донорного полупроводника n₀ = N_D (1.17), тогда

   (1.24) Для акцепторного полупроводника p₀ = N_A (1.19), тогда    (1.25)

1.6. Проводимость полупроводников

При приложении электрического поля к однородному полупроводнику в последнем протекает электрический ток. При наличии двух типов свободных носителей - электронов и дырок - проводимость σ полупроводника будет определяться суммой электронной σ_n и дырочной σ_p компонент проводимости σ=σ_n+σ_p. Величина электронной и дырочной компонент в полной проводимости определяется классическим соотношением:

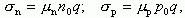   (1.26)

где μ_n и μ_p - подвижности электронов и дырок соответственно.

Для легированных полупроводников концентрация основных носителей всегда существенно больше, чем концентрация неосновных носителей, поэтому проводимость таких полупроводников будет определяться только компонентой проводимости основных носителей. Так, для полупроводника n-типа

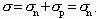   (1.27)

Величина, обратная удельной проводимости, называется удельным сопротивлением:

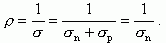   (1.28)

Здесь ρ - удельное сопротивление, обычно измеряемое в единицах [Ом·см]. Для типичных полупроводников, используемых в производстве интегральных схем, величина удельного сопротивления находится в диапазоне ρ = (1-10) Ом·см.

Подставляя соотношение (1.10) в (1.11), получаем

---

где N_D - концентрация доноров в полупроводнике n-типа в условиях полной ионизации доноров, равная концентрации свободных электронов n₀.

В отраслевых стандартах для маркировки полупроводниковых пластин обычно используют следующее сокращенное обозначение типа: КЭФ-4,5. В этих обозначениях первые три буквы обозначают название полупроводника, тип проводимости, наименование легирующей примеси. Цифры после букв означают удельное сопротивление, выраженное во внесистемных единицах, - Ом·см. Например, ГДА-0,2 - германий, дырочного типа проводимости, легированный алюминием, с удельным сопротивлением ρ = 0,2 Ом·см; КЭФ-4,5 - кремний, электронного типа проводимости, легированный фосфором, с удельным сопротивлением ρ = 4,5 Ом·см.

---

1.7. Токи в полупроводниках

Как уже отмечалось выше, проводимость, а следовательно, и ток в полупроводниках обусловлены двумя типами свободных носителей. Кроме этого, также есть две причины, обуславливающие появление электрического тока, - наличие электрического поля и наличие градиента концентрации свободных носителей. С учетом сказанного плотность тока в полупроводниках в общем случае будет суммой четырех компонент:

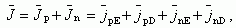   (1.29)

где J - плотность тока, j_nE - дрейфовая компонента электронного тока, j_nD - диффузионная компонента электронного тока, j_pE - дрейфовая компонента дырочного тока, j_pD - диффузионная компонента дырочного тока.

Выражение для каждой из компонент тока дается следующими соотношениями:

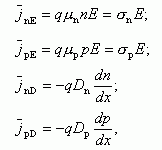   (1.30)

где D_n - коэффициент диффузии электронов, связанный с подвижностью электронов μ_n соотношением . Аналогичные соотношения существуют для коэффициентов диффузии дырок D_p и подвижности дырок μ_p.

1.8. Неравновесные носители

Образование свободных носителей заряда в полупроводниках связано с переходом электронов из валентной зоны в зону проводимости. Для осуществления такого перехода электрон должен получить энергию, достаточную для преодоления запрещенной зоны. Эту энергию электрон получает от ионов решетки, совершающих тепловые колебания. Таким образом, преодоление запрещенной зоны электроном происходит обычно за счет тепловой энергии решетки. Концентрация носителей заряда, вызванная термическим возбуждением в состоянии теплового равновесия, называется равновесной.

Однако помимо теплового возбуждения появление свободных носителей заряда может быть связано с другими причинами, например, в результате облучения фотонами или частицами большой энергии, ударной ионизации, введения носителей заряда в полупроводник из другого тела (инжекция) и др. Возникшие таким образом избыточные носители заряда называются

---