Файл: Научная работа включает 33 страниц, 18 иллюстраций и 3 использованных литературных источников.doc

неравновесными. Таким образом, полная концентрация носителей заряда равна:

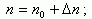   (1.31)

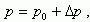   (1.32)

где n₀ и p₀ - равновесная концентрация, а Δn и Δp - неравновесная концентрация электронов и дырок. Если возбуждение избыточных электронов производилось из валентной зоны, а полупроводник однородный и не содержит объемного заряда, то концентрация избыточных электронов равна концентрации избыточных дырок:

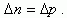   (1.33)

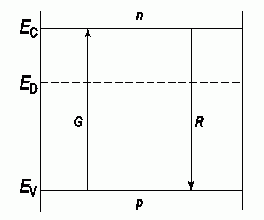
После прекращения действия механизма, вызвавшего появление неравновесной концентрации носителей, происходит постепенное возвращение к равновесному состоянию. Процесс установления равновесия заключается в том, что каждый избыточный электрон при встрече с вакантным местом (дыркой) занимает его, в результате чего пара неравновесных носителей исчезает. Явление исчезновения пары носителей получило название рекомбинации. В свою очередь возбуждение электрона из валентной зоны или примесного уровня, сопровождающееся появлением дырки, называется генерацией носителей заряда.

На рисунке 1.9 G - это темп генерации, а R - темп рекомбинации свободных носителей заряда в собственном полупроводнике.

Рис. 1.9. Генерация и рекомбинация свободных электронов и дырок в полупроводниках

Скорость (темп) рекомбинации R пропорциональна концентрации свободных носителей заряда:

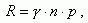   (1.34)

где γ - коэффициент рекомбинации. При отсутствии освещения (в темноте) G=G₀ и , величины n₀ и p₀ иногда называют темновыми концентрациями свободных электронов и дырок соответственно. Из формул (1.30) и (1.14) получим:

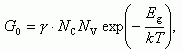   (1.35)

---

где E_g = E_C - E_V - ширина запрещенной зоны. Таким образом, G₀ будет больше в узкозонных полупроводниках и при высоких температурах.

Если в полупроводнике нет электрического тока и объемных зарядов, то изменение во времени неравновесных концентраций электронов и дырок в зонах определяется уравнениями:

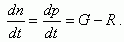   (1.36)

Скорости (темпы) генерации и рекомбинации имеют две составляющие:

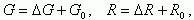   (1.37)

где ΔG, ΔR - темпы генерации и рекомбинации только неравновесных электронов, то есть ΔG - это темп генерации электронов и дырок за счет освещения полупроводника, и . Используя равенство (1.31), (1.32) и (1.34), уравнение (1.36) можно свести к следующему:

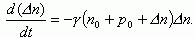   (1.38)

Рассмотрим процесс рекомбинации неравновесных носителей заряда (то есть при выключении освещения в момент времени t = 0). Общее решение уравнения (1.38) довольно сложное. Поэтому рассмотрим два частных случая.

В собственном полупроводнике при сильном освещении . Из (1.38) получим:

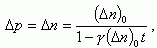   (1.39)

где Δn₀ - начальная концентрация неравновесных носителей заряда. Спад концентрации происходит по параболическому закону.

В донорном полупроводнике в случае полной ионизации доноров n₀ = N_D, p₀ << n₀. Будем также считать, что Δn << N_D. Уравнение (1.38) сводится к виду:

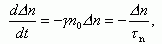   (1.40)

где введено обозначение:

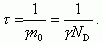   (1.41)

Уравнение (1.40) легко решается:

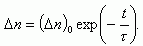   (1.42)

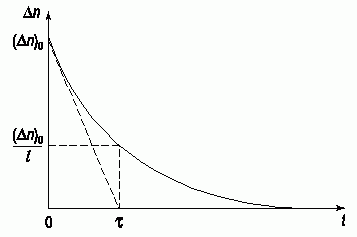
Величина τ имеет смысл среднего времени электронов в зоне проводимости. Полученные решения иллюстрируются на рисунке 1.10. Из (1.42) видно, что процесс рекомбинации описывается экспоненциальной зависимостью от времени, причем среднее время жизни представляет собой такой отрезок времени, за который концентрация избыточных носителей изменяется в "е" раз.

---

В заключение отметим, что неравновесные носители заряда появляются только в том случае, если энергия фотонов при освещении полупроводника превышает ширину запрещенной зоны (hν > E_g).

Рис. 1.10. Спад неравновесной концентрации электронов во времени в донорном полупроводнике

---

1.9. Уравнение непрерывности

Динамика изменения неравновесных носителей по времени при наличии генерации и рекомбинации в полупроводнике, а также при протекании электрического тока определяется уравнением непрерывности. Для полупроводника n-типа уравнение непрерывности будет описывать динамику изменения концентрации дырок p_n:

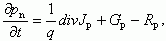   (1.43)

где J_p - дырочный ток, включающий дрейфовую и диффузионную компоненту, G_p - темп генерации неравновесных носителей, а R_p - темп рекомбинации.

Уравнение непрерывности - это уравнение сохранения числа частиц в единице объема. Это уравнение показывает, как и по каким причинам изменяется концентрация неравновесных дырок со временем. Во-первых, концентрация дырок может изменяться из-за дивергенции потока дырок, что учитывает первое слагаемое. Во-вторых, концентрация дырок может изменяться из-за генерации (ударная ионизация, ионизация под действием света и т. д.). В-третьих, концентрация дырок может изменяться из-за их рекомбинации, что учитывает третье слагаемое.

2. Полупроводниковые диоды

Введение

Полупроводниковым диодом называют нелинейный электронный прибор с двумя выводами. В зависимости от внутренней структуры, типа, количества и уровня легирования внутренних элементов диода и вольт-амперной характеристики свойства полупроводниковых диодов бывают различными. В данном разделе будут рассмотрены следующие типы полупроводниковых диодов: выпрямительные диоды на основе p-n перехода, стабилитроны, варикапы, туннельные и обращенные диоды.

2.1. Характеристики идеального диода на основе p-n перехода

Основу выпрямительного диода составляет обычный электронно-дырочный переход. Как было показано в главе 2, вольт-амперная характеристика такого диода имеет ярко выраженную нелинейность, приведенную на рисунке 4.1(а,б), и описывается уравнением (4.1). В прямом смещении ток диода инжекционный, большой по величине и представляет собой диффузионную компоненту тока основных носителей. При обратном смещении ток диода маленький по величине и представляет собой дрейфовую компоненту тока неосновных носителей. В состоянии равновесия суммарный ток, обусловленный диффузионными и дрейфовыми токами электронов и дырок, равен нулю.

---

, (4.1)



Рис. 4.1. Параметры полупроводникового диода

а) вольт-амперная характеристика б) конструкция корпуса

Для анализа приборных характеристик выпрямительного диода важными являются такие дифференциальные параметры, как коэффициент выпрямления, характеристичные сопротивления и емкости диода в зависимости от выбора рабочей точки.

2.2. Выпрямление в диоде

Одним из главных свойств полупроводникового диода на основе p-n перехода является резкая асимметрия вольт-амперной характеристики: высокая проводимость при прямом смещении и низкая при обратном. Это свойство диода используется в выпрямительных диодах. На рисунке 4.2(а) приведена схема, иллюстрирующая выпрямление переменного тока в диоде.

Рассмотрим, каков будет коэффициент выпрямления идеального диода на основе p-n перехода. Для этого рассчитаем по уравнению (4.1) коэффициент выпрямления К как отношение прямого тока к обратному току диода при значениях напряжения U =  0,01 В; 0,025 В; 0,1 В; 0,25 В; 1 B. Получаем:

. (4.2)

Учтем, что величина ^-1 при комнатной температуре составляет ^-1 = 0,025 В. Результаты расчета приведены в следующей таблице.

VG, B	 0,01	0,025	0,1	0,25	1
K, отн. ед.	1,0	1,1

Как следует из таблицы и соотношения (4.2), при значениях переменного напряжения, модуль которого V_G меньше, чем тепловой потенциал kT/q, полупроводниковый диод не выпрямляет переменный ток. Коэффициент выпрямления достигает приемлемых величин при значениях V_G по крайней мере в 4 раза больших, чем тепловой потенциал

---