Файл: Лабораторная работа 1. Основные свойства электрорадиоматериалов 1 Краткая теория.docx

ЛАБОРАТОРНАЯ РАБОТА №1. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРОРАДИОМАТЕРИАЛОВ

1.1 Краткая теория

1.1.1 Электропроводность электрорадиоматериалов

— это физическая величина, которая описывает насколько хорошо определенный материал проводит электричество.

Существует три различных формульных обозначения удельной электропроводности σ (греч. сигма), k (каппа) и γ (гамма). Формула электропроводности, также называемой удельной электропроводностью, описывается формулой:

σ=1/ρ.

Здесь ρ называется удельным сопротивлением. Электрическое сопротивление R проводника с учетом его параметров следующим образом:

R=(ρ·l)/S.

Таким образом, сопротивление R равно удельному сопротивлению ρ, умноженному на длину проводника l, деленному на площадь поперечного сечения S.

Если выразить эту формулу через удельную электропроводность, то σ=1/ρ, полезно знать, что электрическая проводимость G проводника выражается следующим образом: G=1/R .

Если в верхнюю формулу подставить удельную электропроводность σ и электрическую проводимость G, то получится следующее: 1/G=(1/σ) (l/S) .

Путем дальнейшего преобразования можно получить выражение:

G=σ S/l .

С помощью электропроводности можно также описать важную зависимость между плотностью электрического тока и напряженностью электрического поля с помощью выражения: J=σ·E .

1.1.2 Единица измерения удельной электропроводности

Единицей удельной электропроводности σ в СИ является: [σ]=1 См/м (Сименс на метр ).

Эти единицы определяются по формуле G=σ·S/l. Если решить эту формулу в соответствии с σ, то получим σ=G·l/S.

Единица измерения электрической проводимости G задается как: [G]=1/σ=1 См (Сименс, международное обозначение: S).

Если теперь ввести в формулу все единицы измерения, то получится:

[σ]=1 См·1 м / м² = 1 См / м .

В зависимости от количества свободно перемещающихся электронов один материал проводит лучше, чем другой. В принципе, любой материал является проводящим, но в изоляторах, например, протекающий электрический ток ничтожно мал, поэтому здесь мы говорим о непроводниках.

1.1.3 Электропроводность металлов

В металлических связях валентные электроны, т.е. крайние электроны в атоме, свободно подвижны. Они расположены в так называемой полосе проводимости. Находящиеся там электроны образуют так называемый электронный газ. Соответственно, металлы являются сравнительно хорошими проводниками. Если теперь

---

подать электрическое напряжение на металл, валентные электроны медленно движутся к положительному полюсу, потому что он их притягивает.

Для большинства веществ уже известны значения удельной электропроводности. Некоторые из них вы можете найти в следующей таблице. Все значения в этой таблице действительны для комнатной температуры, т.е. 25°C.

Таблица 1.1. Таблица удельной электропроводности некоторых веществ при температуре 25 °C

Вещество	Удельная электропроводность, См / м
Серебро	62 · 106
Медь	58 · 106
Золото	45,2 · 106
Алюминий	37,7 · 106
Вольфрам	19 · 106
Латунь	15,5 · 106
Железо	9,93 · 106
Нержавеющая сталь (WNr. 1,4301)	1,36 · 106
Кремний (легирование <10-12)	0,5 · 10-3
Морская вода	примерно 5
Водопроводная вода	примерно 0,05
Дистиллированная вода	5 · 10-6
Изолятор	обычно <10-8

Удельная электропроводность сильно зависит от температуры, поэтому указанные значения применимы только при 25°C. При повышении температуры вибрация решетки в веществе становится выше. Это нарушает поток электронов, и поэтому электропроводность уменьшается с ростом температуры.

Из таблицы видно, что медь имеет вторую по величине электропроводность, поэтому медные кабели очень часто используются в электротехнике. Серебро обладает еще более высокой проводимостью, но стоит намного дороже меди.

---

Интересно также сравнение между морской и дистиллированной водой. Здесь электропроводность возникает благодаря растворенным в воде ионам. Морская вода имеет очень высокую долю соли, которая растворяется в воде. Эти ионы передают электрический ток. В дистиллированной воде нет растворенных ионов, поэтому в ней практически не может протекать электрический ток. Поэтому электропроводность морской воды намного выше, чем дистиллированной.

---

1.1.4 Деформация проводников

Деформация — это любые изменения структуры, формы, размеров тел. Она происходит под влиянием напряжений - сил, которые действуют на единицу площади сечения заготовок или деталей. Деформация металла обусловлена:

• 
  внешними силами;
  
• 
  усадкой;
  
• 
  структурными превращениями;
  
• 
  внутренними физико-механическими процессами.
  

Под нагрузкой F следует понимать максимальную силу, действующую вдоль оси проволоки, при которой последняя не проявляет признаков разрушения (уменьшения диаметра) [1]. Предельно допустимую нагрузку, при которой проволока еще не разрушается, характеризуют пределом текучести σ_S, который обычно берется из справочника [2] или других источников.

Примеры прилагаемых к телу нагрузок:

• 
  сжатие – нагрузка прикладывается соосно по направлению к телу;
  
• 
  растяжение – возникает при продольном от тела приложении нагрузки (соосно или параллельно плоскости, в которой находятся точки крепления тела);
  
• 
  изгиб – нарушение прямолинейности главной оси тела;
  
• 
  кручение – возникает при приложении к телу крутящего момента.
  

Механизм и виды деформирования изучаются материаловедением, физикой твердого тела, кристаллографией.

1.2 Содержание работы

Целью лабораторной работы является расчет основных параметров проволоки.

Математические расчеты проводятся в удобной для студента программной среде.

Проволока, не претерпевая пластической деформации, должна выдержать нагрузку F, Н. Сопротивление одного метра этой проволоки должно быть не более R, Ом. Плотность сплава линейно зависит от содержания цинка. Предел текучести для латуни Л60 σ_{S Л60} , Н/м², для латуни Л80 σ_{S Л80}, Н/м², для меди σ_Cu, Н/м².

Определить;

1. 
   Наименьший диаметр d_min проволоки, изготовленной из латуней Л60, Л80, из чистой меди?
   
2. 
   Какая проволока окажется наиболее экономически выгодной, если считать, что медь вдвое дороже цинка?
   
3. 
   Диаметр проволоки по сопротивлению d_R.
   
4. 
   
   

Исходные данные приведены в таблице 1.1. (Приложение 1)

---

1.3 Порядок выполнения работы

1.3.1 Деформация проволоки

1. 
   По формуле (1.1) вычисляем требуемое сечение проволоки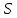
   

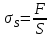(1.1)

2. 
   По формуле (1.2.) рассчитываем радиус
   

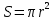. (1.2)

3. 
   Проведя элементарные преобразования определяем наименьший диаметр d_min
   
4. 
   Построить графики зависимости d_minотпредела текучести вещества
   

1.3.2 Диаметр по сопротивлению

1. 
   Из справочных материалов определяем удельную электропроводность меди .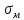
   
2. 
   Относительная электропроводность относительно чистой латуни:
   

• 
  латуни Л60  для ;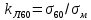
  
• 
  латуни Л80 .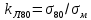
  

Осуществляем расчет 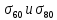для относительно чистой меди (Л60 и Л80).

3. 
   Из формулы (1.3) находим удельное сопротивление ρ
   

σ=1/ρ. (1.3)

4. 
   Из (1.4.) получаем требуемый диаметр по сопротивлению d_R
   

R=(ρ·l)/S (1.4)

где 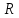– сопротивление отрезка проволоки;

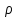– удельное сопротивление (по справочным данным);

l – длина проводника;

S – площадь сечения.

5. 
   d_R – диаметр по сопротивлению определяется из S.
   
6. 
   Результаты расчета оформить в виде таблиц 1.2, 1.3. (Приложение 1)
   
7. 
   Построить графики зависимости Rпровода от его сечения.
   

1.3.3 Расчет расстояния от источника напряжения до места повреждения изоляции

В двухпроводной линии электропередачи, на одном конце которой находится источник постоянного напряжения, а с другой подключена нагрузка с сопротивлением R (50 Ом), повредилась изоляция, в результате чего ток в источнике вырос в n₁ раза, а ток в нагрузке упал в n₂ раз. На каком расстоянии x от источника произошло повреждение изоляции, если удельное сопротивление единицы длины проводящих проводов равно ρ₁, а длина линии электропередачи равна L

---