Файл: Контрольная работа по предмету Статистика Проверил 2021 Оглавление Задача 3.docx

Тогда дисперсия выборки

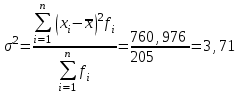
Предельная ошибка выборки вычисляется как: ,

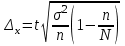где 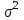является выборочной дисперсией.

t – нормированное отклонение, зависящее от вероятности,

n – объем выборки,

N – объем генеральной совокупности.

.

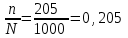При вероятности 0,997 коэффициент доверия t=3

Тогда предельная ошибка выборки:



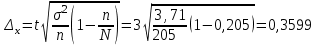
Определим границы генеральной средней:





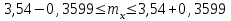
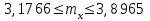
Следовательно, генеральная средняя продолжительность стажа равна 3,54±0,36 года или попадает в интервал: 3,183,90
2) Найдём пределы доли рабочих со стажем до 2 лет

Всего в выборке рабочих со стажем, не превышающим 2 лет, 45 человек.

Возможные пределы, в которых ожидается доля рабочих со стажем свыше 8 лет, определим по формуле:



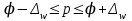
где 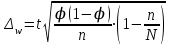– предельная ошибка выборочной доли.

t – нормированное отклонение, зависящее от вероятности,

n – объем выборки,

N – объем генеральной совокупности.



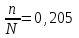
Выборочная доля рабочих со стажем до 2 лет

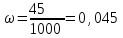
Дисперсия стажа рабочих равна 3,71 кг.

При вероятности 0,954 коэффициент доверия t=2.

Предельная ошибка выборочной доли:



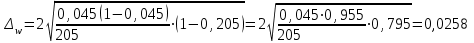
С помощью предельной ошибки выборочной доли определим границы для доли рабочих со стажем до 2 лет:





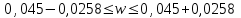
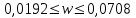
Доля рабочих со стажем до 2 лет в генеральной совокупности попадает интервал (0,0192; 0,0708)

Задача 8.4.

По данным задачи 1 рассчитайте ранговый коэффициент корреляции Спирмена между среднесписочной численностью работающих и прибылью организаций.

---

Решение:

Обозначим как X среднесписочную численность работающих, как Y – прибыль предприятий.

Присвоим ранги признаку Y и фактору X.

Ранги, их разность и квадраты разместим в таблице.

Среднесписочная численность работающих (X)	Прибыль, тыс. руб. (Y)	RX	RY	d=RX–RY	d2
606	2878	18	20	-2	4
360	1062	9	12	-3	9
641	3858	19	21	-2	4
587	2593	17	17	0	0
264	324	4,5	4	0,5	0,25
490	1174	16	14	2	4
386	1922	11	15	-4	16
405	1988	13	16	-3	9
377	754	10	6	4	16
441	1029	15	10	5	25
344	1042	8	11	-3	9
268	178	6	3	3	9
1017	90	21	1	20	400
670	2698	20	18	2	4
159	137	1	2	-1	1
390	2868	12	19	-7	49
		231	231		622,5

---

Контрольная сумма:

Сумма по столбцам R_X и R_Y равны между собой и равны контрольной суммы, значит, ранги определены верно.

Вычислим коэффициент ранговой корреляции Спирмена. Поскольку среди значений Y встречаются одинаковые, т.е. образуются связанные ранги, то в коэффициент Спирмена вычисляется как:



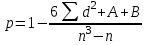
где , ,

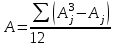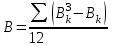j – номера связок по порядку для признака X;

А_j – число одинаковых рангов в j-й связке по X;

k – номера связок по порядку для признака Y;

В_k – число одинаковых рангов в k-й связке по Y.





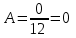
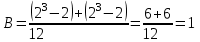
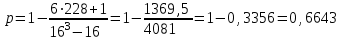
Связь между признаком Y и фактором X умеренная и прямая.



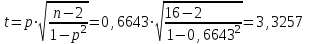
Расчетное значение статистики Стьюдента сравним с табличным при уровне значимости 0,05 и числе степеней свободы v = n – 2 = 16 – 2 = 14: t_крит= 2,51.

2,51 < 3,3257

Следовательно, коэффициент корреляции Спирмена статистически значим.

Значит, между среднесписочной численностью работающих и прибылью имеется прямая умеренная связь.

Задача 8.5.

Имеются следующие данные о средних запасах оборотных средств предприятия по месяцам за 2017 год (ден. ед.):

Месяцы	Запасы	Месяцы	Запасы	Месяцы	Запасы
1.	217	5.	219	9.	197
2.	218	6.	215	10.	206
3.	207	7.	197	11.	190
4.	210	8.	193	12.	194

---

Произведите аналитическое выравнивание ряда динамики по прямой. Сделайте выводы о характере общей тенденции изучаемого явления. Сделайте прогноз запасов на январь 2018 г.
Решение:

Для выравнивания ряда динамики по прямой используют уравнение

у_t = a₀ + a₁t.

Параметры а₀ и а₁ можно найти способом наименьших квадратов, в котором параметры находятся из системы двух нормальных уравнений:



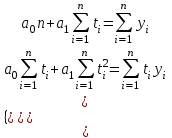
где у – исходные (эмпирические) уровни ряда динамики;

n – число членов ряда;

t – время.
Придадим показателям времени t такие значения, чтобы их сумма была равна нулю, т.е. ∑t = 0.

Произведем расчет необходимых значений в таблице:

месяц	y	t	t2	yt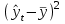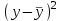
1	217	-11	121	-2387	218,19	1,42	485,13	434,03
2	218	-9	81	-1962	215,84	4,67	387,01	476,69
3	207	-7	49	-1449	213,49	42,07	299,96	117,36
4	210	-5	25	-1050	211,13	1,28	223,99	191,36
5	219	-3	9	-657	208,78	104,45	159,09	521,36
6	215	-1	1	-215	206,43	73,50	105,27	354,69
7	197	1	1	197	204,07	50,03	62,52	0,69
8	193	3	9	579	201,72	76,04	30,84	10,03
9	197	5	25	985	199,37	5,60	10,24	0,69
10	206	7	49	1442	197,01	80,75	0,72	96,69
11	190	9	81	1710	194,66	21,72	2,27	38,03
12	194	11	121	2134	192,31	2,86	14,89	4,69
	2463	0	572	-673	2463,00	464,42	1781,92	2246,33

---

В этом случае решение системы нормальных уравнений:





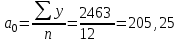
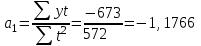
Уравнение тренда:

y_t = 205,25 – 1,1776t
Коэффициент тренда a₁ = –1,776 показывает среднее изменение запасов оборотных средств предприятия в 2017 г. с изменением периода времени на месяц. В данном случае с увеличением периода t на 1 месяц, запасов оборотных средств предприятия в 2017 г. (y) уменьшается в среднем на 1,1776 ден. ед.

Судя по отрицательному коэффициенту тренда, запасы оборотных средств уменьшаются со временем.

Оценим (сделаем прогноз) запасы на январь 2018 г.

Для января 2018 г. показатель времени t = 13, используя уравнение тренда, определяем: y(13)= 205,25 – 1,177613= 189,95 ден. ед.

Задача 8.6.

По данным таблицы определите индивидуальные и агрегатные индексы физического объема продукции, цен и стоимости. Объясните, что означают полученные индексы.

Виды продукции	Ед. измерения	Объем продукции		Цена за единицу продукции, ден. ед.
		базисный период	отчетный период	базисный период	отчетный период
А	шт.	575	525	175	195
Б	м3	1750	1150	205	255

Решение:

Введем обозначения:

p₀, p₁– цена продукции А в базовый и отчетный периоды соответственно,

q₀, q₁– физический объем продукции А в базовый и отчетный периоды соответственно.

Индивидуальный индекс цен рассчитаем по формуле:



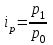
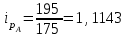или 111,43% 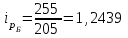или 124,39%

В отчетном периоде в наибольшей степени выросла цена на продукцию Б – прирост составил 24,39%, цена на продукцию А выросла 11,43%.

---