Файл: Задача 1 4 Решение 5 Задача 2 7 Решение 9 Задача 3 9 Решение 10 Задача 4 11 Решение 12 Задача 5 13.docx
Добавлен: 12.12.2023
Просмотров: 254
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решение
-
По таблице 2.1 вычислим входные запросы на обслуживание X(t) = 6,509 и вычислим выходной поток предоставленных услуг Y(t) = 4,041. -
По таблице 2.2 вычислим входные запросы на обслуживание X(t) = 6,569 и вычислим выходной поток предоставленных услуг Y(t) = 4,441. -
По таблице 2.3 вычислим входные запросы на обслуживание X(t) = 6,634 и вычислим выходной поток предоставленных услуг Y(t) = 4,021. -
По таблице 2.4 вычислим входные запросы на обслуживание X(t) = 6,097 и вычислим выходной поток предоставленных услуг Y(t) = 3,887.
В ходе выполнения задачи №2 мы нашли аналитическое выражение, связывающее входные и выходные потоки в системе обслуживания – почтовом предприятии связи.
Результаты вычислений представлены в таблице:
| Коэффициент | Таблица 2.1 | Таблица 2.2 | Таблица 2.3 | Таблица 2.4 |
| | 0,620833 | 0,676054 | 0,60612 | 0,637527 |
Задача 3
Результатом исследования почтового предприятия связи явилось построение аналитической модели, позволяющей оценить относительную продолжительность (R) процедуры обслуживания клиентов в течение одного часа.
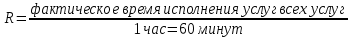
По истечении рабочего периода хронометража получены данные, помещенные в таблице 3-1 (вариант 3).
Таблица 3-1.
| Номер варианта | Показатель загруженности операторов в течение 8-часового рабочего дня (R) | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 3 | 0,56841 | 0,06684 | 0,27684 | 0,35684 | 0,47684 | 0,16684 | 0,37684 | 0,46684 |
Указание:
В данной задаче отыскивается решение индивидуально – каждым участником учебной группы.
Требуется вычислить дисперсию относительного времени исполнения услуги. Вычисления исполняются каждым участником учебной группы, в соответствии с индивидуальным номером зачетной книжки.
Искомая оценка вычисляется по выражению:
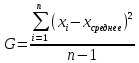
Полученная оценка для каждого варианта дополняется комментариями, характеризующими адекватность проведенного исследования.
Решение
Первым делом найдем
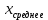 по формуле =СРЗНАЧ(B4:I4) и получим значение 0,34454. Примем n = 24.
по формуле =СРЗНАЧ(B4:I4) и получим значение 0,34454. Примем n = 24. В ходе выполнения задачи №3 мы поэтапно вычислили дисперсию относительного времени исполнения услуги.
Результаты вычислений представлены в таблице:
| x | x-x_среднее | (x-x_среднее)^2 | (x-x_среднее)^2/n-1 |
| 0,56841 | 0,2238729 | 0,0501191 | 0,0021791 |
| 0,066841 | -0,2776961 | 0,0771151 | 0,0033528 |
| 0,276841 | -0,0676961 | 0,0045828 | 0,0001993 |
| 0,356841 | 0,0123039 | 0,0001514 | 0,0000066 |
| 0,476841 | 0,1323039 | 0,0175043 | 0,0007611 |
| 0,166841 | -0,1776961 | 0,0315759 | 0,0013729 |
| 0,376841 | 0,0323039 | 0,0010435 | 0,0000454 |
| 0,466841 | 0,1223039 | 0,0149582 | 0,0006504 |
Задача 4
Для принятия формально обоснованного решения о проведенном исследовании хронометража рабочего времени операторов почтового предприятия связи, осуществляется вычисление доверительного интервала рабочего времени – на контролируемом промежутке в 8 часов. С этой целью используется выражение:
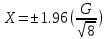
В решении этой задачи используются индивидуальные данные предыдущей задачи.
Указания.
-
Полученное значения Х (формула записана выше) сопоставляется с пороговым значением, определяющим достоверность проведенных исследований. Полагать, что если текущая оценка превосходит пороговое значение, то такое исследование рекомендуется повторить.
В противном случае полученный результат принимается, а само исследование полагается проведенным корректно. Для проведения процедуры сопоставления воспользоваться данными, помещенными в таблице 4-1.
Вариант 3 – пороговые значения 0,020019.
-
Сформулировать выводы. Пояснить полученный результат. В выводах указать насколько велика разница базовой и вычисленной оценки.
Указание: В данной задаче отыскивается решение индивидуально – каждым участником учебной группы.
Решение
Для принятия формально обоснованного решения о проведенном исследовании хронометража рабочего времени операторов почтового предприятия связи, осуществляется вычисление доверительного интервала рабочего времени – на контролируемом промежутке в 8 часов.
С этой целью по выражению
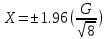 рассчитаем X(-) и X(+) по данным из таблицы предыдущей задачи.
рассчитаем X(-) и X(+) по данным из таблицы предыдущей задачи. Результаты вычислений представлены в таблице:
| X(-) | -0,00152544 | -0,00234710 | -0,00013948 | -0,00000461 | -0,00053277 | -0,00096106 | -0,00003176 | -0,00045527 |
| X(+) | 0,00152544 | 0,00234710 | 0,00013948 | 0,00000461 | 0,00053277 | 0,00096106 | 0,00003176 | 0,00045527 |
X(-) = -0,00152544 и X(+) = 0,00152544 сопоставим с пороговым значением 0,020019, определяющим достоверность проведенных исследований.
Полагаем, что если текущая оценка превосходит пороговое значение, то такое исследование рекомендуется повторить. В нашем случае текущая оценка не превосходит пороговое значение 0,020019.
-
Разница между X(-) = -0,00152544 и 0,020019 составляет 0,02154444. -
Разница между X(+) = 0,00152544 и 0,020019 составляет 0,01849356.
Следовательно полученный результат принимается, а само исследование полагается проведенным корректно.
Задача 5
Для сопоставления рабочей загруженности нескольких предприятий связи создается модель. Количественное (численное) исследование модели позволяет установить поток исполненных услуг: принятых почтовых переводов (a), выданных почтовых переводов (b), приобретенных конвертов (c) и открыток (d), выданных бандеролей e) и т.д.
Каждая процедура, рассматриваемая как отдельная услуга, характеризуется численным показателем. Набор численных показателей в течение 8 часов работы предприятия связи (период исследования) создавался для трех предприятий. Данные по исследованию модели почтового предприятия связи представлены в таблицах 5-1 – 5-4.
Указание. Учебная группа делится на 4 части. Каждая подгруппа анализирует один из 4 вариантов задачи
Требуется найти коэффициент корреляции между тремя моделями предприятий. Вычисления провести по выражению:
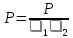
Где
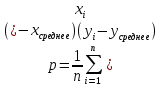
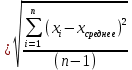
Построить графические зависимости, поясняющие полученные результаты.