Файл: Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 41
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание
Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид: x(t) =
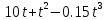
Найти:
-
Среднюю скорость Vср за интервал времени от t1 до t2; t1=2.4 c; t2=14.1 с; -
Среднюю путевую скорость Vср.п. за тот же интервал времени; -
Среднее ускорение.
Построить графики зависимостей х(t) и Vx(t).
Краткие теоретические сведения:
Явление, изучаемое в ргз – прямолинейное движение материальной точки.
Определение основных величин, процессов, явлений, объектов:
Тело отсчета – произвольно выбранное тело, относительно которого определяется положение движущейся материальной точки (или тела).
Система отсчета – это совокупность тела отсчета, системы координат и системы отсчета времени, связанных с этим телом, по отношению которого изучается движение (или равновесия) каких-либо других материальных точек или тел.
Координата – это совокупность чисел или независимых переменных, которые определяют положение точки в пространстве.
Материальная точка – это тело, размерами, которых можно пренебречь по сравнению с расстоянием до других тел.
Траектория – линия, которую описывает материальная точка при своем движении. Если точка двигаясь по траектории переместилась из точки 1 в точку 2, то это расстояние называется длиной пройденного частицей пути или просто пройденным частицей путем.
Перемещение – вектор, проведенный из начального положения частицы в конечное.
Скорость - векторная величина, характеризующая быстроту движения и его направление в данный момент времени.
Мгновенная скорость - векторная физическая величина, равная пределу отношения перемещения тела к промежутку времени, в течение которого это перемещение произошло.
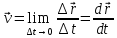
Мгновенная скорость v, таким образом, есть векторная величина, определяемая первой производной радиуса-вектора движущейся точки по времени.
Модуль мгновенной скорости равен первой производной пути по времени:
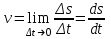
Единица скорости [м/с].
Средняя скорость - равна отношению перемещения тела к промежутку времени, за который это перемещение произошло. Является векторной величиной.
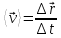
Средняя путевая скорость - это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден. Является скалярной величиной.
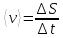
Ускорение – производная скорости по времени
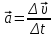 .
.Законы, соотношения, использованные при решении
Модуль скорости:
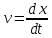
Средняя скорость
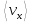 за интервал времени
за интервал времени 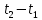 определяется выражением
определяется выражением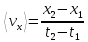
Средняя путевая скорость за время от
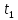 до
до 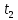 :
: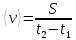
Ускорение равно первой производной скорости по времени:
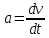
Пояснение ко всем величинам, входящим в формулы и соотношения:
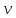 – мгновенная скорость в данный момент времени
– мгновенная скорость в данный момент времени
; [
 ]=м/с.
]=м/с.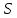 – путь, пройденный материальной точки; [
– путь, пройденный материальной точки; [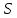 ]=м.
]=м.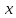 – перемещение материальной точки; [
– перемещение материальной точки; [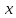 ]=м.
]=м. – средняя скорость, [
– средняя скорость, [ ]=м/с.
]=м/с.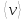 – средняя путевая скорость, [
– средняя путевая скорость, [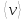 ]=м/с.
]=м/с.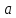 – ускорение, [
– ускорение, [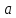 ]=м/с2.
]=м/с2.Расчеты:
1) S = x(t2) – x(t1) – путь пройденный телом, будет равен разности конечной и начальной его координат.
x(t1) =
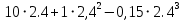 =27,69 (м); - координата тела в момент врем
=27,69 (м); - координата тела в момент врем 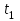
x(t2) =
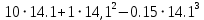 = -80,67 (м); - координата тела в момент времени
= -80,67 (м); - координата тела в момент времени 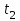 .
.S = -80,67 – 27,69 = -108.36 (м); - путь пройденный телом.
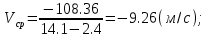 - средняя скорость.
- средняя скорость.2) Путь пройденный материальной точкой за промежуток времени от t1 – t2
S = 2 × xmax – x1 – x2
3) Определим xmax
Найдём сначала производную от координаты по времени и приравняем её к нулю
V = 10 + 2tmax - 0.45tmax 2 = 0
Далее найдём t
max
tmax = -0.52 : -0.9 =0.57 с
получаем максимальную координату:
xmax = x(tmax) =
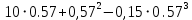 = 6 м
= 6 м Подставим полученные значения в формулу
S = 2
 6 – 27.69 + 80.67 = 64.98
6 – 27.69 + 80.67 = 64.98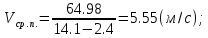
3) Найдём среднее ускорение:
a =
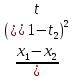 =
= 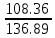 = 0.792 (м/с2)
= 0.792 (м/с2) Так как ускорение непостоянно, то найдём производную по скорости, чтобы показать его зависимость от времени.
a = Vꞌ(t) = 2 - 0.9t
Графики.
График зависимости x(t): x(t)=

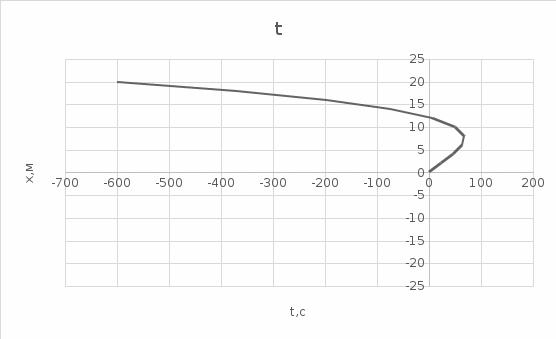
График зависимости a(t):
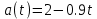
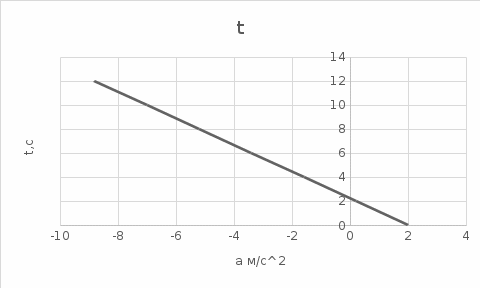

Окончательный ответ:
1)
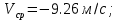
2)
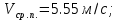
3) a = 0.792 м/с2.
Вывод.
В результате проделанной работы можно сказать, что при данном кинематическом уравнении движения материальной точки по прямой точка двигалась сначала равноускоренно, затем остановилась и начала равнозамедленное движение в обратную сторону. В расчетах были использованы основные физические формулы движения материальной точки по прямой и дифференцирование.