Файл: Курсовая работа Игра Точки и квадраты.docx

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ им. Р.Е.АЛЕКСЕЕВА

Институт радиоэлектроники и информационных технологий

Кафедра информатики и систем управления
Курсовая работа

Игра «Точки и квадраты»
по дисциплине

Алгоритмы и структуры данных

РУКОВОДИТЕЛЬ:

________________ Капранов С. Н.

СТУДЕНТ:

________________ Сухоруков В.А.


19-ИВТ-3

Работа защищена «___» ____________

С оценкой ________________________


Нижний Новгород 2020

Оглавление

Правила игры

Игровое поле представляет из себя n рядов по n точек. Играющие соединяют соседние по вертикали или горизонтали точки отрезками. Ходы делаются по очереди, но если игрок замкнул своим ходом один или два единичных квадратика, то он закрашивает эти квадраты своим цветом, и он обязан продолжать делать ходы, пока не сделает ход, не замыкающий квадратик, или до конца игры. Когда проведены все отрезки

---

, подсчитываются квадратики, которые замкнул каждый игрок. Выигрывает тот, кто занял больше точек.

Инструкция пользователя

Программа разработана для игры в «Точки и квадраты». Исходное поле представляет собой поле точек, в крайних двух противоположных углах располагаются точки компьютера и Ваша: в левом нижем компьютера, в правом верхнем Ваша.

Цель игры заключается в захвате незанятых точек. Побеждает тот, кто соберёт больше.

Если игрок собирает квадрат, то его противник пропускает ход.

Соединять можно любую занятую Вами точку с точкой, не принадлежащей противнику и расположенной рядом с данной (сверху, снизу, справа или слева).

Координаты точки – 2 значения от 0 до 9.

Инструкция программиста

Файл Tree.h содержит структуру узла дерева и функции для работы с ней. Поля структуры:

struct Tree_node {

Tree_node* child[N]; //Массив указателей на сыновей

Tree_node* parent; //Указатель на родителя

Tree_node* next_brother; //Указатель на следующего брата

int field [10][10] ; //Состояние поля игры

int connections[10][10][4]; //Массив клеток, соединённых с данной

int count_connections[10][10];//Количество клеток, соединённых с данной

int count_child; //Количество сыновей

int number; //Номер узла

int height; //Высота узла

int assessment; //Оценка текущего состояния игры

int alpha; //Параметр для альфа-бета отсечения

int betta; //Параметр для альфа-бета отсечения

int count_check_child; //Количество просмотренных сыновей при

//поиске лучшего хода

bool is_check; //Был ли полностью рассмотрен узел т.е.

//рассмотрены все его сыновья

bool is_square; //Показывает был ли образован квадрат на

//этом ходу

};

Функции:

1. 
   Tree_node* newNode //Позволяет создавать узел с переданными
   

//параметрами

2. 
   void push(]); //Позволяет добавлять сына узлу с
   

//переданными номером

3. 
   void deletion(); //Позволяет освободить динамическую
   

//память выделенную под дерево

Код основного файла содержит функции логики игры:

1. 
   bool game_is_over(); //Проверяет завершенность игры
   
2. 
   bool check_cell(); //Проверяет можно ли занять клетку
   
3. 
   void is_square(); //Проверяет был ли образован квадрат
   

//на данном ходу

4. 
   void generation_move(); //Генерирует ход
   
5. 
   void make_tree(); //Строит дерево возможных ходов
   
6. 
   void get_assessment(); //Оценочная функция
   
7. 
   void alpha_betta(); //Алгоритм альфа бета отсечения
   
8. 
   void choose_best_move(); //Выбирает лучший ход
   
9. 
   void Print_field(); //Выводит поле игры
   
10. 
    Tree_node* creat_root(); //Создаёт начальный корень дерева
    
11. 
    Tree_node * re_create_root();//Создаёт корень дерева
    
12. 
    void read_human_move(); //Считывает ход игрока
    
13. 
    Tree_node* game(); //Осуществляет игровой процесс
    
14. 
    void get_result(); //Анализ результатов игры
    

---

---

Оценочная функция

Описание оценочной функции

Каждая точка на игровом поле имеет свою стоимость, её значение может быть отрицательным или положительным, в зависимости от принадлежности игроку. Если точка принадлежит компьютеру, то её стоимость положительная, если человеку – отрицательная. Если точка не принадлежит игроку, то её стоимость равна нулю. Результат оценочной функции – сумма стоимостей каждой точки.

Стоимость точки определяется её связями с соседними "‎союзными "‎ точками: модуль значения стоимости точки равен количеству её связей.

П 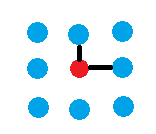ример: Красная точка принадлежит компьютеру и имеет 2 связи с соседними точками. Её стоимость – 2.

Пример расчёта оценочной функции

1. 
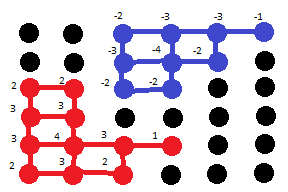
   Рассчитываем стоимость каждой клетки.
   
2. 
   Вычисляем значение оценочной функции.
   

F=2+2+3+3+3+4+3+1+2+3+2-2-3-3-1-3-4-2-2-2=6

Программная реализация оценочной функции

/*Оценочная функция

Параметры:

1)Указатель на узел дерева, поля которого:

1. 
   int field[10][10]- текущее состояние поля
   
2. 
   int count_connections[10][10]- количество связей клетки
   
3. 
   assessment - оценка поля
   

Принцип работы:

1)Просматриваются значения клеток текущего поля

2)Если значение клетки равно 1, то она принадлежит компьютеру. К результату прибавляется количество связей этой клетки

3)Если значение клетки равно 2, то она принадлежит человеку. К результату вычитается количество связей этой клетки

*/

void get_assessment(Tree_node* PNode) {

int res = 0;

for (int i = 0; i < 10; i++) {

for (int j = 0; j < 10; j++) {

if (PNode->field[i][j] == 1) {

res = res + PNode->count_connections[i][j];

}

if (PNode->field[i][j] == 2) {

res = res - PNode->count_connections[i][j];

}

}

}

PNode->assessment = res;

}

Алгоритм минимакса

Описание вычислений

Алгоритм Минимакса — правило принятия решений, используемое в теории игр, теории принятия решений, исследовании операций, статистике и философии для минимизации возможных потерь их тех

---

, которые лицу, принимающему решение, нельзя предотвратить при развитии событий по наихудшему сценарию.

Строится дерево ходов (решений) заданной глубины. После постройки дерева получаем результаты оценочной функции для каждого листа (состояния поля) и начинаем двигаться вверх, к корню дерева. На уровне MIN выбирается минимальное значение дочерних узлов и транслируется на данный уровень, а на уровне MAX максимальное значение дочерних узлов. Последними операциями выбора и трансляции получаем значение для корня дерева. Как только получено значение корня дерева делаем ход согласно той ветви, которая привела к данному результату. Если к одинаковому значению корня приводят несколько ветвей дерева, то направления движения выбирается произвольно.

Пример расчёта

Рассмотрим состояние поля, представленное на скриншоте 1. Ход делает компьютер (MAX – красные точки).



Скриншот 1

Для данного состояния возможно построение следующего дерева минимакса.



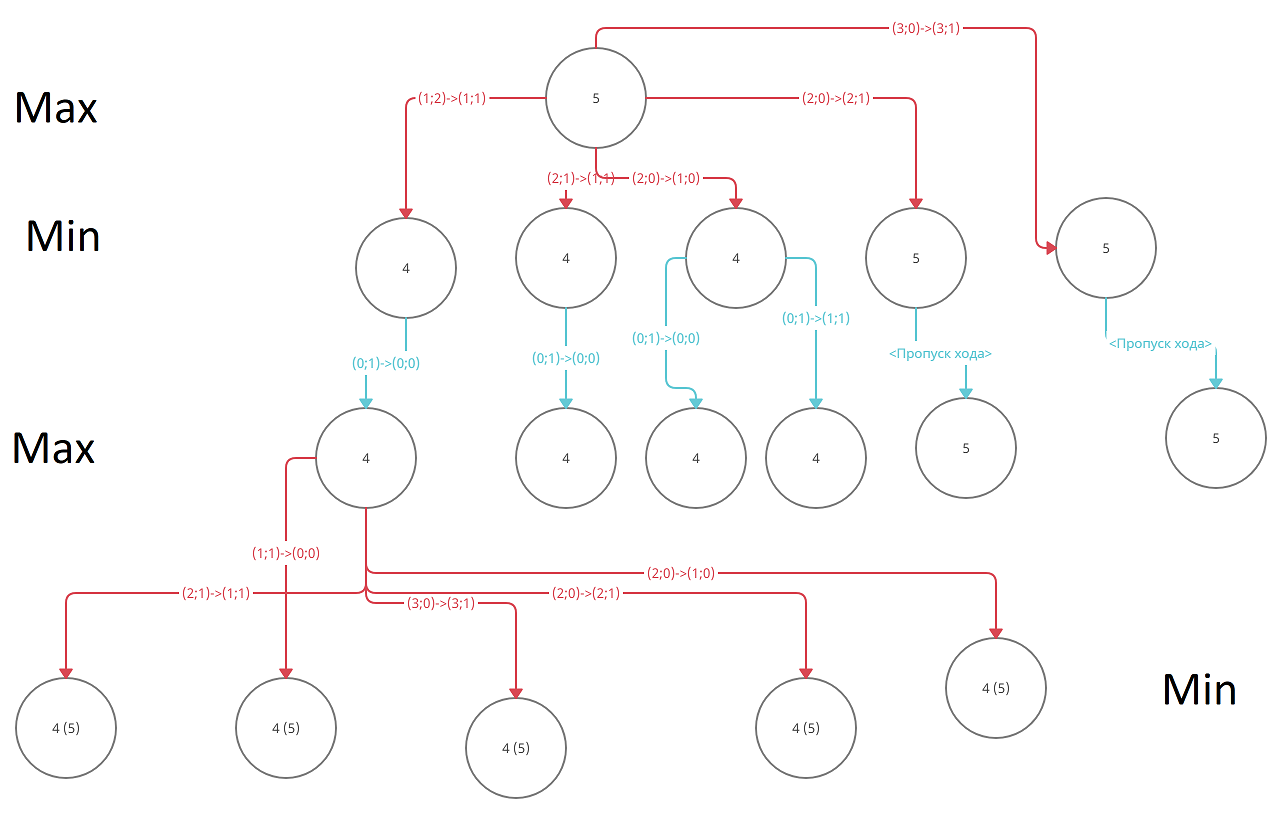
Замечание: Последний уровень у всех вершин одинаковый, для отсутствия нагромождения он построено только для одной вершины.

В дереве красным цветом отмечены ходы компьютер, синим ходы игрока.

Программная реализация

/*Функция минимакса

Параметры:

1)Указатель на узел дерева

Принцип работы:

1)Если узел является листом, то высчитываем его оценку

2)Если проверены не все сыновья узла, то применяем функция к непроверенным сыновьям

4)Вычисляем значение проверенных сыновей

5)Если проверены все сыновья, то узел проверен

6)Если узел не корень:

6.1) Если родитель находится на чётном уровне (минимума) и его значение больше оценки текущего узла, то заменяем оценку

6.2) Если родитель находится на нечётном уровне (максимума и его значение меньше оценки текущего узла, то заменяем оценку

*/

void Min_max(Tree_node* PNode) {

if (PNode->height == 3) {

get_assessment(PNode);

}

if (PNode->count_check_child != PNode->count_child) {

for (int i = PNode->count_check_child;

i count_child; i++)

{

Min_max(PNode->child[i]);

}

}

for (int i = 0; i < PNode->count_child; i++) {

if (PNode->child[i]->is_check == true) {

PNode->count_check_child++;

}

}

if (PNode->count_check_child == PNode->count_check_child) {

PNode->is_check = true;

}

if (PNode->height != 1) {

if (PNode->parent->height % 2 == 0) {

if (PNode->parent-> assessment > PNode->assessment)

PNode->parent-> assessment = PNode->assessment;

}

if (PNode->parent->height % 2 == 1) {

if (PNode->parent-> assessment < PNode->assessment) {

PNode->parent-> assessment = PNode->assessment;

}

}

if (PNode->next_brother != nullptr) {

PNode = PNode->next_brother;

}

else {

PNode = PNode->parent;

}

}

}

1   2   3   4   5   6   7   8   9   10

---