ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 1034
Скачиваний: 10
СОДЕРЖАНИЕ
БӚЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР Алгебра
«Екі айнымалысы бар теңдеулер,теңсіздіктер және олардың жүйелері»
Бағалау критерииі: Білім алушы:
Бағалау критерииі: Білім алушы:
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«Ықтималдықтар теориясының элементтері»
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
VI тоқсанға арналған ТЖБ
| Орындау уақыты: | 40 минут |
І нұсқа
-
[2 балл] Екі ойын сүйегі лақтырылды.Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 7 болу ықтималдығын табыңыз.
-
[5 балл] Урнада 3 ақ және 6 қара шарлар бар.
-
Урнадан бір уақытта екі шар алынады. Олар бірдей түсті болу ықтималдығын табыңыз. -
Бір уақытта екі шарды алып тастағанда, қандай оқиға болуы мүмкін А «бір түсті шарлар», В – «түрлі түсті шарлар»?
-
[2 балл] Бұйымдардың сапасын тексеру үшін 200 бӛлшектер зерттелді,олардың ішінде 8 ақаулы болды.
а) наугад алынған бӛлшектің жарамды болуы ықтималдығын табыңыз.
b) 1000 бӛлшектен тұратын партияда орташа ақаулы бӛлшектер қанша болады?
-
[3 балл] Радиус шеңберінің ішінде R наудачу нүкте тасталған. Нүкте шеңберге жазылған квадрат ішінде болуы ықтималдығын табу. Шеңбердің бӛлігіне нүктенің құлау ықтималдығы осы бӛліктің алаңына пропорционалды және оның шеңберге қатысты орналасуына байланысты емес деп болжанады.
-
[3 балл] Ӛрнекті ықшамдаңыз: sin 2 3cos 2 2 cos 2 3sin 2 2 .
-
[5 балл] Тепе-теңдікті дәлелдеңіз:
cos cos 2tg .
1sin 1 sin
ІІ нұсқа
-
[2 балл] Екі ойын сүйегі лақтырылды.Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 8 болу ықтималдығын табыңыз.
-
[5 балл] Урнада 5 ақ және 3қара шарлар бар.
-
Урнадан бір уақытта екі шар алынады. Олар бірдей түсті болу ықтималдығын табыңыз. -
Бір уақытта екі шарды алып тастағанда, қандай оқиға болуы мүмкін А «бір түсті шарлар», В – «түрлі түсті шарлар»?
-
[2 балл] Бұйымдардың сапасын тексеру үшін 500 бӛлшектер зерттелді,олардың ішінде 9 ақаулы болды.
а) наугад алынған бӛлшектің жарамды болуы ықтималдығын табыңыз.
b)1000 бӛлшектен тұратын партияда орташа ақаулы бӛлшектер қанша болады?
-
[3 балл] Радиус шеңберінің ішінде R наудачу нүкте тасталған. Нүкте шеңберге жазылған квадрат ішінде болуы ықтималдығын табу. Шеңбердің бӛлігіне нүктенің құлау ықтималдығы осы бӛліктің алаңына пропорционалды және оның шеңберге қатысты орналасуына байланысты емес деп болжанады.
-
[3 балла] Ӛрнекті ықшамдаңыз : 2sin 3 3cos 3 2 2cos 3 3sin 3 2 .
-
[5 баллов] Тепе-теңдікті дәлелдеңіз:
sin sin 2ctg .




Балл қою кестесі:
І нұсқа
| № | Жауап | Балл | Қосымша ақпарат |
| 1 | (2;5), (1;6) | 1 | |
| (5;2), (6;1) | 1 | ||
| 2(a) | C92 , C32 , C62 | 1 | Ең болмағанда бір дұрыс жазуға балл қою |
| С2 С2 3! 6! 3 6 1!2! 4!2! | 1 | ||
| С2 С2 1 Р( А) 36 С2 2 9 | 1 | ||
| 2(b) | С1С1 3 6 | 1 | Қабылданады балама жауап |
| P(B) P(A) | 1 | ||
| 3(а) | 2008 0,975 200 | 1 | |
| 3 (b) | 1000 5; 58 40 200 | 1 | |
| 4 | ???? = 2????2 | 1 | |
| 2????2 P = ????????2 | 1 | ||
| P = 2 ???? | 1 | ||
| 5 | ????i????22???? + 6????i????2????????????????2???? + 9????????????22???? + ????????????22???? − −6????i????2????????????????2???? + 9????i????22???? | 1 | |
| Мұндай қосылыстарды келтіреді | 1 | ||
| 1+9=10 | 1 | ||
| 6 | coscosasincossincos 2tg 1sin 2 | 1 | |
| Мұндай қосылғыштарды келтіріңіз. Негізгі тригонометриялық тепе-теңдікті қолданады | 1 | ||
| 2cossin 2tg cos2 | 1 | ||
| 2 ????i???? ???? = 2???????????? ???????????? ???? | 1 | ||
| 2tgα=2tgα | 1 | ||
| Барлығы | 20 | | |
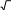
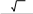
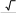
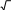
ІІ нұсқа
| № | Жауап | Балл | Қосымша ақпарат |
| 1 | (3;5), (5;3) | 1 | |
| (2;6), (6;2) (4;4) | 1 | ||
| 2(a) | C82 , C52 , C32 | 1 | Ең болмағанда бір дұрыс жазуға балл қою |
| С2 С2 5! 3! 13 5 3 (5 2)!2! (3 2)!2! | 1 | ||
| С2 С2 13 Р( А) 53 С2 28 8 | 1 | ||
| 2(b) | С1С1 15 5 3 | 1 | Қабылданады балама жауап |
| С2 С2 15 Р(В) 53 С2 28 8 P(B) P(A) | 1 | ||
| 3(а) | 5009 0,982 500 | 1 | |
| 3 (b) | 1000 2; 2 9 18 500 | 1 | |
| 4 | а 2Rsin 60o R3 a3 (R3 )3 3 3 2 S R 4R 4R 4 | 1 | |
| P Sтр 33 R3 1 S 4 R2 кр | 1 | ||
| P 33 4 | 1 | ||
| 5 | 4sin2 3 12sin 3 cos 3 9 cos2 3 4 cos2 3 12sin 3 cos 3 9sin2 3 | 1 | |
| Мұндай қосылыстарды келтіреді | 1 | ||
| Ӛрнек мәнін табады =13 | 1 | ||
| 6 | sinsincossinsincos 2ctg 1 cos2 | 1 | |
| Мұндай қосылғыштарды келтіріңіз. Негізгі тригонометриялық тепе-теңдікті қолданады | 1 | ||
sin2 | 1 | ||
sin | 1 | ||
| 1 | ||
| Барлығы: | 20 | | |