Файл: Фин. Вычисления 1.doc

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«Тольяттинский государственный университет»
Институт финансов, экономики и управления

^{(наименование института полностью)}

⁽^{Наименование учебного структурного подразделения}⁾

38.03.03

^{(код и наименование направления подготовки / специальности)}

Управление персоналом

^{(направленность (профиль) / специализация)}

Практическое задание № 1
по учебному курсу «Финансовые вычисления 2»

^{(наименование учебного курса)}

Обучающегося	^{Н.А Поганов}
	^{(И.О. Фамилия)}
Группа	УПбвд-2001а

Преподаватель	Морякова Анастасия Владимировна
	^{(И.О. Фамилия)}

Тольятти 2022
Содержание

Практическое задание 1 2

Практическое задание 2 4

Практическое задание 3 5

Практическое задание 4 6

Практическое задание 5 7

Практическое задание 6 8

Список использованной литературы 9

Практическое задание 1

Тема 2. Простые и сложные проценты

Задание

Кредит размером 1,2 млн руб. выдан 15 февраля до 7 ноября включительно под 17 % годовых. Какую сумму должен вернуть должник в конце срока, если начисляются простые проценты. При решении задачи используйте три способа расчета простых процентов:

Первый способ. Начисление точных процентов с точным числом дней ссуды.

Второй способ. Начисление обыкновенных процентов с точным числом дней ссуды.

Третий способ. Начисление обыкновенных процентов с приближенным числом дней ссуды.
Дано:

0,17 – простая годовая процентная ставка;

1,2 млн. руб. – первоначальная сумма;

15 февраля – дата начала финансовой операции;

7 ноября – дата окончания финансовой операции;

Найти:

– наращенную сумму.

Решение:

Существует три способа начисления по простым процентам:

1. Точные проценты с точным числом дней ссуды.

Продолжительность года Y (временная база) равна 365 (366) дням. Точное число дней ссуды t определяется путем подсчета числа дней между датой выдачи ссуды и датой ее погашения. Точное число дней между 15 февраля и 7 ноября (год невисокосный) составляет t = 265 дней.

Расчет наращенной суммы:

тыс. руб.
2. Обыкновенные проценты с точным числом дней ссуды.

Величина t рассчитывается как в предыдущем случае, а временная база принимается равной Y= 360 дням. Расчет наращенной суммы:

тыс. руб.
3. Обыкновенные проценты с приближенным числом дней ссуды.

В этом случае год делится на 12 месяцев, по 30 дней в каждом и временная база Y = 360 дням. Приближенное число дней между 15 февраля и 7 ноября составляет t = 262 дня.

Расчет наращенной суммы:

тыс. руб.

Ответ. Наращенная сумма при точных процентах с точным числом дней составит 1348,110 тыс. руб., по обыкновенным процентам с точным числом дней – 1350,167 тыс. руб., по обыкновенным процентам с приближенным числом дней – 1348,467 тыс. руб.

Для должника наиболее предпочтительный вариант – точные проценты с точным числом дней ссуды. т.к. наращенная сумма минимальна.

Практическое задание 2

Тема 2. Простые и сложные проценты

Задание

Клиент открыл счет в банке и поместил на него сумму в размере 25 000 руб. Сложная годовая процентная ставка 11 %. Через два года и 164 дня клиент закрыл счет. Определите двумя методами, какую сумму получил клиент в случае начисления точных процентов. Какой метод расчета предпочтительнее для клиента, а какой выгоднее для банка?
Дано:

0,11 – сложная годовая процентная ставка;

25 000 руб. – первоначальная сумма;

лет – срок финансовой операции в годах;

года - целое число лет;

- дробная часть года.

Найти:

– наращенную сумму двумя методами.

Решение:

Наращенная сумма при расчете первым способом составит:

32 281,24 руб.

Расчет наращенной суммы при смешанном способе начисления процентов (второй способ):

32 324,90 руб.

Ответ. Наращенная сумма при использовании 1-го метода составит 32281,24 руб.; при использовании 2-го метода – 32324,90 руб. Для клиента предпочтительнее 2-й метод, т.к. наращенная сумма больше.

Практическое задание 3

Тема 3. Оценка денежных потоков

Задание

Ежегодно в течение 6 лет на банковский счет в конце года поступает 12 000 руб. На эти средства ежеквартально начисляются проценты по номинальной ставке 15 % годовых. Рассчитайте, какая сумма будет накоплена на банковском счете к концу указанного срока. Определите, как изменится итоговая сумма, если начисление процентов будет происходить ежемесячно.

Дано:

=12 000 руб. - размер равного годового платежа;

0,15 – сложная номинальная процентная ставка;

4 – число периодов начислений процентов в год;

6 лет – срок ренты.

12 – число периодов начислений процентов в год.

Найти:

– наращенную сумму ренты при

.

Решение:

Расчет наращенной суммы ренты:

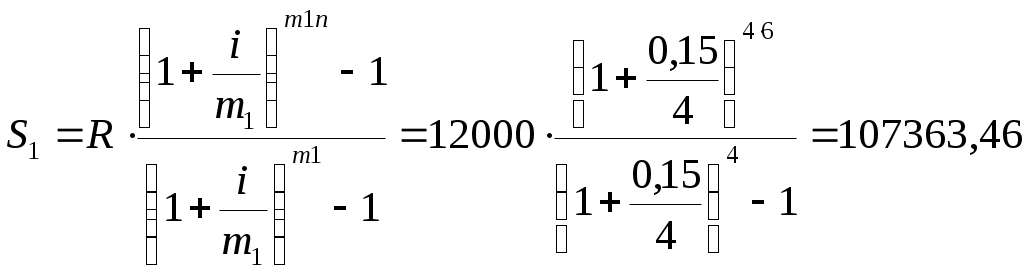
Если начисление процентов будет происходить ежемесячно, то:

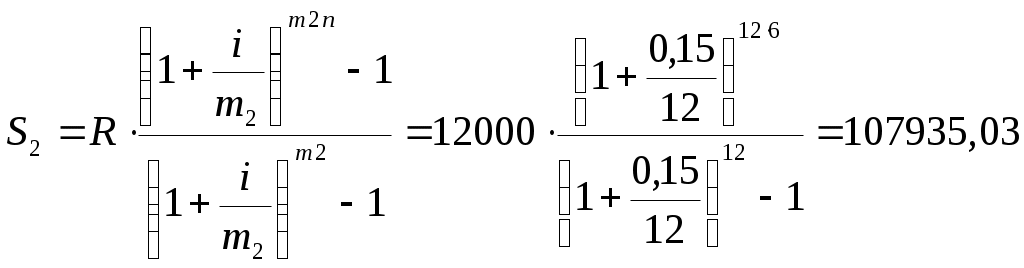
Ответ. При ежеквартальном начислении процентов наращенная сумма ренты составит 107363,46 руб.; при ежемесячном начислении – 107935,03 руб. При начислении процентов ежемесячно итоговая сумма будет на 571,56 руб. больше. Для клиента выгоднее ежемесячное начисление процентов.

Практическое задание 4

Тема 4. Финансовые активы

Задание

Для облигации номиналом 10 500 руб., выпущенной на 3 года, определен следующий порядок выплат: первый год – 10 %; далее каждый год процентная ставка повышается на 1,5 %. Определите наращенную стоимость облигации. Как изменится эта сумма, если процентная ставка в первый год начисления составит 12 %.
Дано:

= 10 500 руб. – номинальная стоимость облигации

0,1,

0,115,

0,13 – переменные процентные ставки;

1 – сроки начисления по процентным ставкам.

0,12,

0,135,

0,15 – измененные переменные процентные ставки.

Найти:

– наращенную стоимость облигации.

Решение:

Расчет наращенной стоимости облигации:

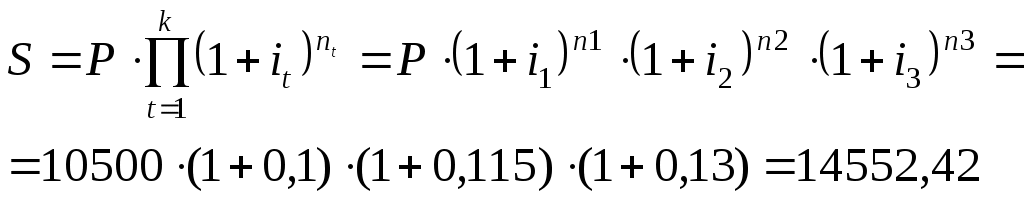
Расчет наращенной стоимости облигации, если процентная ставка в первый год начисления составит 12 %:

Ответ. Наращенная стоимость облигации при ставках наращения 10%, 11,5% и 13% составит 14552,42 руб. А при ставках 12%, 13,5% и 15% наращенная сумма составит 15349,74 руб.

Практическое задание 5

Тема 5. Финансовые ренты

Задание

Четыре платежа в размере 25 000 руб. в конце первого года, 20 000 руб. в конце второго года, 35 000 руб. в конце третьего года, 40 000 руб. в конце четвертого года образуют ренту постнумерандо. Размер годовой процентной ставке 18 %. Определите наращенную сумму финансовой ренты постнумерандо к концу четвертого года. На сколько изменится эта сумма, если размер годовой процентной ставки увеличится на 3%.
Дано: