ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 207
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Учебно-методическое пособие
тема: « ЛОГАРИФМЫ »
Дисциплина: «МАТЕМАТИКА»
Аннотация:
Учебно-методическое пособие по теме «ЛОГАРИФМЫ» предназначено для организации аудиторной и самостоятельной работы обучающихся 1 курса средних профессиональных учебных заведений, осуществляющих обучение на базе основного общего образования. Пособие предназначено для реализации государственных требований к минимуму содержания и уровню подготовки студентов по дисциплине «Математика».
В пособии содержится большое количество практических заданий. Предложенные задания закрепляют полученные обучающимися теоретические знания по теме: «Логарифмы», позволяют им освоить навыки решения разбора различных логарифмических выражений с подробным изучением основных формул, а так же изучить различные методы решения логарифмических уравнений, применяемые в каждом конкретном случае.
Оглавление
Пояснительная записка 4
Откуда взялся Log? 7
Свойства логарифмов 9
Дифференцированный набор заданий по теме «Понятие логарифма» 11
Свойства логарифмов (образцы решения) 14
Набор заданий для систематизации знаний 22
Дифференцированный набор заданий для систематизации знаний «Свойства логарифма» 27
Образцы решения логарифмических уравнений 36
Набор заданий для систематизации знаний для решения логарифмических уравнений 52
Лист контроля по теме: «Логарифмическая функция» 54
Количество вариантов: 55
Заключение 56
Приложение1 57
«Изобретение логарифмов, сократив работу астронома, продлило ему жизнь»
П.С.Лаплас
Пояснительная записка
Учебно-методическое пособие по теме «ЛОГАРИФМЫ» предназначено для преподавателей математики и обучающихся 1 курса средних профессиональных учебных заведений, осуществляющих обучение на базе основного общего образования. Пособие предназначено для реализации государственных требований к минимуму содержания и уровню подготовки студентов по дисциплине «Математика».
Учебно–методическое пособие создано в связи с недостаточным количеством раздаточного материала
, применяемого при изучении темы: «Логарифмы».
Пособие интересно тем, что для изучения, закрепления, а так же контроля разработаны и подобраны материалы разных видов.
Данное методическое пособие поможет студентам при изучении логарифмов. В пособии приводятся определение логарифма, свойства, основные формулы, а также примеры решения логарифмов, логарифмических выражений.
Работая с данным пособием, студенты будут четко знать основные способы решения логарифмов и логарифмических выражений, уметь быстро определять нужную формулу.
Данное методическое пособие могут использовать в своей работе и преподаватели с целью организации аудиторной и самостоятельной работы :
-
систематизации, закрепления и углубления полученных теоретических и практических знаний, умений; -
формирования умений применять теоретические знания; -
развития самостоятельности и организованности студентов;
Использование пособия на различных этапах занятия предполагает экономию времени и усилий (преподавателя, студента) за счет компактного изложения теоретического материала; иллюстрации каждой формулы примерами; подробно разобранных заданий; упражнений подобранных в системе.
Учебно - методическое пособие позволит студентам с наибольшей эффективностью организовать свою деятельность по подготовке к успешной сдаче экзамена.
Оценка качества выполнения студентами заданий будет осуществляться поэтапно, в соответствии с планом занятий по пятибалльной шкале.
Критерии оценок:
Отметка «5» ставится, если:
-
работа выполнена полностью; -
в логических рассуждениях и обосновании решения нет пробелов и ошибок; -
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
-
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки); -
допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Отметка «3» ставится, если:
-
допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
-
допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
-
работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Откуда взялся Log?
Мы изучили показательные уравнения. Давайте повторим, решив одно из них.
Запишем данное уравнение так:
Напомним, что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 2.
А теперь, попробуем решить еще одно показательное уравнение.
Теперь, тех знаний с точки зрения решения показательных уравнений, недостаточно.
Есть ли корень у этого показательного уравнения? Да, есть.
Как его найти, если уравнение не решается привычным способом?
И теперь, мы введем понятие «логарифм», которое поможет нам решить данное уравнение.
Важно запомнить!
Логарифм (от греч. λόγος – «слово», «отношение», άριθμός - «число») определяется как показатель степени, в которую надо возвести основание, чтобы получить число.
Для начала, представим наши показательные уравнения в виде стандартной формы (т.е. заменим числа с правой и левой стороны на а и b),
напишем:
Важно запомнить!
Корень х уравнения
х =
Соотнесем теперь определение логарифма с (1) показательным уравнением:
х = 5, так как
Значит,
= 32.
Мы решили показательное уравнение с помощью применение логарифма.
Теперь, представим (2) показательное уравнение в виде логарифма и попробуем решить его:
х =
Так откуда же взялся логарифм? А он взялся из-за потребности решить показательное уравнение, которое не решается привычным способом.
Свойства логарифмов
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ЛОГАРИФМИЧЕСКИХ И ПОКАЗАТЕЛЬНЫХ ВЫРАЖЕНИЙ
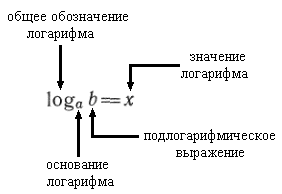
Логарифмом числа bпо основанию а
Основное логарифмическое тождество
| Общая схема вычисления логарифмов. Она состоит из трех шагов:
| | |
| Задача Вычислите логарифм: Решение: Представим основание и аргумент как степень двойки Составим и решим уравнение: Ответ: | Задача Вычислите логарифм: Решение: Представим основание и аргумент как степень тройки: Составим и решим уравнение: 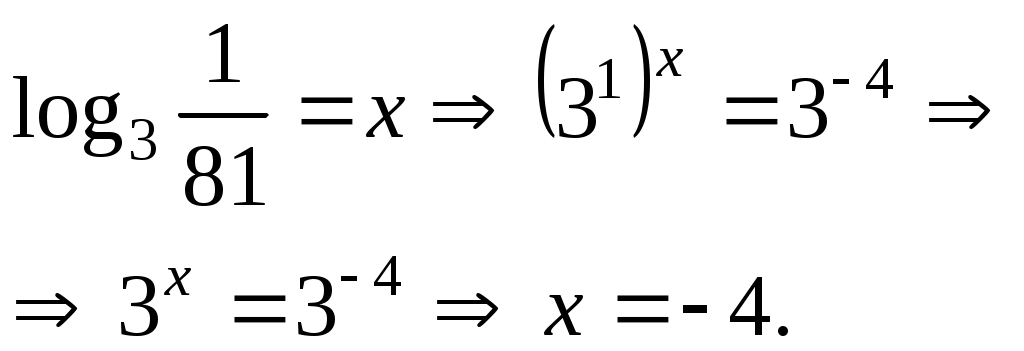 Ответ: | |
| Задача Вычислите логарифм: Решение: Представим основание и аргумент как степень двойки Составим и решим уравнение: Ответ: | Задача Вычислите логарифм: Решение: Представим основание и аргумент как степень пятерки: Составим и решим уравнение: Ответ: | |
| Задача Вычислите логарифм: Решение: Представим основание и аргумент как степень семерки: Ответ: | ||