Файл: логарифмы.doc

Свойства логарифмов (образцы решения)

Другие виды обозначения логарифмов:

логарифм числа b по основанию e

(натуральный логарифм)



e = 2,718281828459045… – основание натурального логарифма;

логарифм числа b по основанию 10

(десятичный логарифм)



10 – основание десятичного логарифма.

Логарифмическая единица

и логарифмический ноль

— это логарифмическая единица.

Запомните раз и навсегда:

логарифм по любому основанию от самого этого основания равен единице.

Например: .

— это логарифмический ноль.

Основание может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому, что

---

— это прямое следствие из определения.

Например: .

Сложение и вычитание логарифмов
Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают.
Задача Представьте логарифм в виде суммы: Решение: Представим число 14 в виде произведения и применим формулу суммы: Ответ:	Задача Найдите значение выражения: Решение: Поскольку основания у логарифмов одинаковые, используем формулу суммы: Ответ:
Задача Представьте логарифм в виде разности: Решение: Представим число 0,4 в виде обыкновенной дроби и применим формулу разности: Ответ:	Задача Найдите значение выражения: Решение: Поскольку основания у логарифмов одинаковые, используем формулу разности: Ответ:

---

Вынесение показателя степени из логарифма

Задача Найдите значение выражения: Решение: Избавимся от степени в аргументе по пятой формуле: Ответ:

Задача Найдите значение выражения: Решение: Избавимся от степени в основании по шестой формуле: Ответ:

Задача Найдите значение выражения: Решение: Избавимся от степени в аргументе и основании по седьмой формуле: Ответ:

Задача Найдите значение выражения: Решение: Избавимся от степени в аргументе по пятой формуле: Ответ:

Задача Найдите значение выражения: Решение: Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: Имеем: Ответ:

Задача Найдите значение выражения: Решение: Избавимся от степени в аргументе по пятой формуле: Ответ:

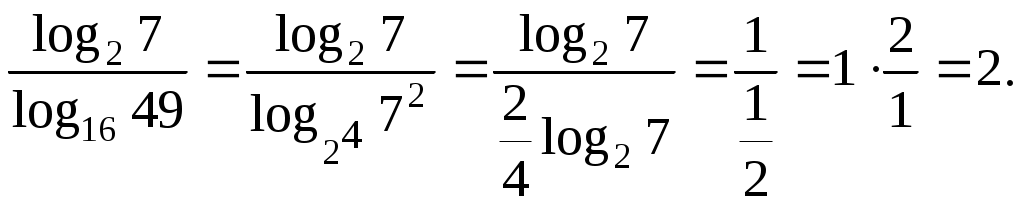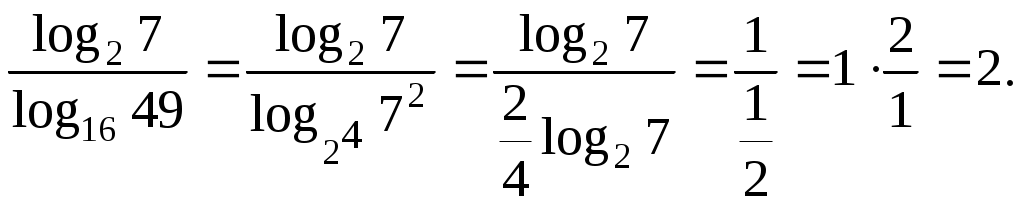Задача Найдите значение выражения: Решение: Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: Имеем: Ответ:

---

Переход к новому основанию

Из девятой формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.

Задача Представьте в виде логарифма с основанием 2. Решение: Воспользуемся восьмой формулой: Ответ:

Задача Представьте в виде логарифма с основанием 7. Решение: Воспользуемся девятой формулой: Ответ:

Задача Найдите значение выражения: Решение: Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: А теперь «перевернем» второй логарифм: 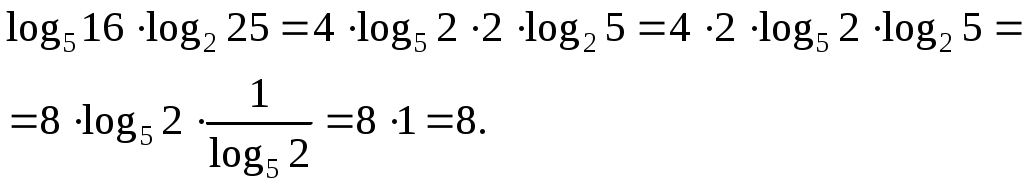Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами. Ответ:
Задача Найдите значение выражения: Решение: Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей: Теперь избавимся от десятичного логарифма, перейдя к новому основанию: Ответ:
Основное логарифмическое тождество
Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:
В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма	Вторая формула — это фактически перефразированное определение. Она так и называется: основное логарифмическое тождество
Задача Найдите значение выражения: Решение: Применяя основное логарифмическое тождество, получаем: Ответ:
Задача Найдите значение выражения: Решение: Заметим, что — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем: Ответ:

---

---