ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 13.08.2024
Просмотров: 50
Скачиваний: 0
4. Принцип доминирования по Парето.
Этот принцип применяется в моделях принятия решений по нескольким критериям.
Пусть альтернативы а1, а2,… аn оцениваются по нескольким (двум) критериям: К1 и К2.
Если альтернатива ai равносильна альтернативе aj по критерию К1, то
ai ~1 aj
Если альтернатива ai равносильна альтернативе aj по критерию К2, то
ai ~2 aj
Если альтернатива ai предпочтительнее альтернативы aj по критерию К1, то
![]()
Если альтернатива ai предпочтительнее альтернативы aj по критерию К2, то
![]()
Если альтернатива ai не хуже альтернативы aj по критерию К1, то
![]()
Если альтернатива ai не хуже альтернативы aj по критерию К2, то
![]()
Пусть
ai
~1
aj
и
![]()
Следовательно, ai доминирует по Парето альтернативу aj
Пусть
ai
~2
aj
и
![]()
Следовательно, ai доминирует по Парето альтернативу aj
В общем случае принцип доминирования по Парето является способом попарного сравнения всех альтернатив. Логически возможны следующие случаи:
1. по всем критериям альтернативы ai и aj эквивалентны, тогда альтернативы ai и aj эквивалентны с точки зрения принятия решений
2. по одним критериям альтернативы ai и aj эквивалентны, а по другим ai предпочтительнее альтернативы aj , тогда ai доминирует по Парето альтернативу aj
3. по одним критериям ai предпочтительнее альтернативы aj , а по другим – ai хуже альтернативы aj , тогда альтернативы ai и aj несопоставимы по Парето.
Пример:
Инвестор должен выбрать один из альтернативных способов размещения активов.
Каждый способ (альтернатива) определяется средним ожидаемым доходом (mi) и риском – средним квадратичным отклонением (σi), где i – номер альтернативы.
Требуется отбросить заведомо плохие альтернативы и составить множество для выбора.
Решение:
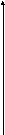
р
 иск
А5
иск
А5


А3 А4
 А2
А2

А1
Ожидаемый доход
Рис.1 «Доминирование по Парето в задаче принятия решения с риском»
Аi(mi, σi)
Сравниваем альтернативы попарно.
Сравним А1 и А2
Имеем: А1~mА2 А1>σА2, так как σ1>σ2
Следовательно А2 – доминируемая стратегия и её можно исключить
Аналогично сравниваем остальные стратегии и получаем, что стратегия А3 – доминируемая, следовательно её тоже отбрасываем
Мы отбросили стратегии А2 и А3 – доминируемые. Инвестор может выбирать из альтернатив А1, А4, А5.
Итак, принцип доминирования по Парето позволяет отбросить доминируемые альтернативы и оставить для рассмотрения множество по Парето несопоставимых альтернатив, называемые альтернативами эффективными по Парето.
Таким образом, принцип доминирования по Парето облегчает задачу принятия решения. Для задачи выбора альтернативы по двум критериям средний ожидаемый доход (mi) и риск ri множество альтернатив, эффективных по Парето, будет лежать на кривой с положительным наклоном:
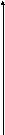
р иск
иск

 А3
А3
 А2
А2

А1
Ожидаемый доход
Рис. 2 «Альтернативы эффективные по Парето»
5. Принятие решений в условиях риска по интегральному критерию
Задача принятия решения с риском содержит Ai, оцененную по mi – средний ожидаемый доход, σi – риск.
Пусть применим принцип доминирования по Парето и получим множество альтернатив эффективности по Парето:
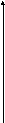
σi


 А3
А3
 А2
А2

А1
mi
рис. 3
Необходимо выбрать наилучшую альтернативу из множества на рисунке 3.
Для этого применяется интегральный (агрегированный) критерий. В общем случае, если альтернативы оцениваются по двум критериям: К1 и К2.
Интегральный критерий – это функция двух переменных:
f(K1,K2)
Возможны различные варианты вида функции.
Например, f(K1,K2)=К1α*К2(1–α) или f(K1,K2)=α*К1+β*К2
α–значимость критерия К1
β– значимость критерия К2
Естественно требование удовлетворения интегрального критерия следующим свойствам:
Если альтернативы ai и aj эквивалентны по всем критериям, то значения интегрального критерия для этих альтернатив равны (и наоборот)
Если ai доминирует по Парето альтернативу aj, то значение интегрального критерия для ai больше соответствующего значения для аj (и наоборот)
Составим линейный интегральный критерий для случая, когда первый критерий – средний ожидаемый доход, а второй – риск:
f(m, σ) = α*m – β* σ
m – средний ожидаемый доход
σ – риск
α≥0 и β ≥0
Пусть α >0, следовательно, агент принимает во внимание ожидаемый доход
Тогда имеем при делении на α:
![]()
λ = β / α >0
Или
f(m, σ) = m – λ * σ ,
λ = const≥0
Раскроем смысл постоянной величины λ.
Если для ЛПР значение λ равно нулю (λ =0), тогда f(m, σ) = m.
Это значит, что субъекта интересует только доход.
Это нейтральность к риску ЛПР.
Если есть два экономических субъекта, таких, что:
Для первого: f1(m, σ) = m – σ , то есть λ1 =1
Для второго: f2(m, σ) = m – 2* σ, то есть λ2 =2
Можно сделать вывод, что второй субъект более чувствителен к риску.
Если предположить, что f(m, σ) = m + σ
Это означает, что данный экономический агент склонен к риску
Таки образом λ отражает отношение ЛПР к риску:
λ =0 нейтральность
λ <0 склонность к риску
Чем больше λ, тем чувствительнее субъект к риску
Пример:
Для ЛПР λ=3.
Оценить с помощью неравенства Чебышева его гарантированную вероятность, на которую ориентируется ЛПР.
Решение:
![]()
ЛПР имеет отклонение X от M(X) на величину больше, чем α.
f(m, σ) = m – 3* σ, следовательно неприятности начинаются при
α. = 3* σ
Имеем,
![]()
Вероятность неприятностей должна быть не больше 1/9. Следовательно данный ЛПР выбирает гарантированную вероятность равную 8/9.
Заметим, что мы действовали как вольные интерпретаторы, то есть полученное решение не строго математическое.