ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.05.2019
Просмотров: 617
Скачиваний: 1
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Кубанский государственный технологический университет»
Кафедра электротехники и электрических машин
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В ЭЛЕКТРОТЕХНИКЕ
Методические указания по выполнению лабораторных работ для студентов очной формы обучения направления 13.03.02 Электроэнергетика и электротехника
Краснодар
2
015
Составители: канд. техн. наук, доц. И.Н. Автайкин
канд. техн. наук, доц. Я.М. Кашин,
Математическое моделирование в электротехнике: методические указания по выполнению лабораторных работ для студентов очной формы обучения направления 13.03.02 Электроэнергетика и электротехника /Сост.: И.Н. Автайкин, Я.М. Кашин; Кубан. гос. технол. ун-т., каф. электротехники и электрических машин. – Краснодар, 2015. – 50с.
Методические указания содержат краткие теоретические сведения, необходимые для выполнения лабораторных работ, описание лабораторных установок, содержание и порядок выполнения работ, содержание отчета и контрольные вопросы для допуска и защиты лабораторных работ. Приведен список литература
Ил. 21. Табл. 12, Библиогр.: 5 назв.
Рецензенты: доц. каф. ЭиЭМ, канд. техн. наук, А.М. Квон
доц., канд. техн. наук, зам директора ЗАО Спецэнергостроймонтаж" И.В. Лежепёков
Содержание
Введение
Современная электроэнергетическая система (ЭЭС) представляет собой сложную систему, имеющую большое число элементов и подсистем. Исследование таких систем невозможно без применения математического моделирования и ЭВМ. Математические модели широко используются для решения электроэнергетических задач.
Математическая модель ЭЭС – это совокупность математических формул или уравнений, определяющих взаимосвязь между параметрами режима ЭЭС.
В ходе выполнения лабораторных работ студент должен изучить методы построения и анализа математических моделей электрических систем, проектируемых с помощью вычислительной техники.
Перед выполнением лабораторной работы внимательно изучить указания по технике безопасности.
1 Основные понятия, термины, определения
1.1 ЭЭС – совокупность электростанций, электрических и тепловых сетей, соединённых между собой и связанных общностью режимов в непрерывном процессе производства, преобразования, передачи и распределения электрической и тепловой энергии при общем управлении этим режимом.
1.2 Математическая модель – математическое представление реальности, один из вариантов модели, как системы, исследование которой позволяет получать информацию о некоторой другой системе. Процесс построения и изучения математических моделей называется математическим моделированием.
1.3 Режим работы ЭЭС – совокупность процессов, происходящих в системе и определяющих в любой момент времени состояние параметров режима.
1.4 Топологический метод - обобщенный метода анализа установившихся рабочих режимов сложных схем замещения электрических цепей на базе применения аппарата матриц и элементов топологической теории графов.
К работе в кабинете информатики допускаются только студенты, прошедшие инструктаж по технике безопасности, соблюдающие указания преподавателя, расписавшиеся в журнале регистрации инструктажа.
Строго запрещается:
-
включать без разрешения оборудование;
-
трогать разъемы соединительных кабелей и проводов (возможно поражение электрическим током);
-
прикасаться к питающим проводам и устройствам заземления;
-
прикасаться к экрану и к тыльной стороне монитора, клавиатуры;
-
включать и выключать аппаратуру без указания преподавателя;
-
работать в верхней одежде и влажными руками;
-
прыгать, бегать (пылить);
-
класть диски, книги, тетради и другие предметы на монитор и клавиатуру;
-
устанавливать или копировать программы с дисков и флеш-носителей на компьютер;
При появлении запаха гари немедленно прекратите работу, выключите аппаратуру и сообщите об этом преподавателю.
Во время работы:
-
строго выполняйте все указанные выше правила, а также текущие указания преподавателя;
-
следите за исправностью аппаратуры и немедленно прекращайте работу при появлении необычного звука или самопроизвольного отключения аппаратуры;
-
легко и быстро нажимайте на клавиши, не допуская резких ударов;
-
не пользуйтесь клавиатурой и мышью, если не включен компьютер;
-
работайте на клавиатуре чистыми руками;
никогда не пытайтесь самостоятельно устранить неисправность в работе аппаратуры.
3. Лабораторная работа №1
РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Целью работы является изучение методов и алгоритмов нахождения корней нелинейных уравнений.
Содержание работы
1. Метод деления отрезка пополам (метод бисекции);
2. Метод секущих (хорд);
3. Метод простых итераций;
4. Метод Ньютона (касательных);
Перечень необходимых материалов, приборов, оборудования
Лабораторная работа проводится в компьютерном классе с сетевым оборудованием со следующим программным обеспечением: ОС MS Windows XP и выше, офисный пакет OpenOffice, система инженерных и математических расчетов MathCad.
Методические указания
1. Метод деления отрезка пополам (метод бисекции)
Допустим, что на отрезке [а,b], расположено искомое значение корня х=с, т. е. с ϵ [а,b]. В качестве начального приближения корня с0 принимаем середину этого отрезка:
Далее исследуем значения функции F(x) на концах отрезков [а, со] и [со,b], т.е. в точках а, со, b. Тот из отрезков, на концах которого F(x) принимает значения разных знаков, содержит искомый корень; Допустим, что нам удалось найти отрезок [а,b], на котором расположено искомое значение корня поэтому его принимаем в качестве нового отрезка [a1,b1]. Вторую половину отрезка [а,b], на которой знак F(x) не меняется, отбрасываем. В качестве первого приближения корня принимаем середину нового отрезка
и т. д.
Таким образом, k-е приближение вычисляется как
После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после k - итераций он сокращается в 2к раз:
Иллюстрация данного метода приведена на рисунке 1.
Процесс вычислений завершается,
когда длина текущего интервала становится
меньше заданной величины точности -
нахождения корня.

Рисунок 1.1 Графическая интерпретация нахождения корней
2. Метод секущих (хорд)
В этом методе кривая f(x) заменяется прямой линией – хордой, стягивающей точки (a, f(a)) и (b, f(b)). В зависимости от знака выражения f(a)*f //(a) метод хорд имеет два варианта, изображенных на рис. 1.2 а, б.
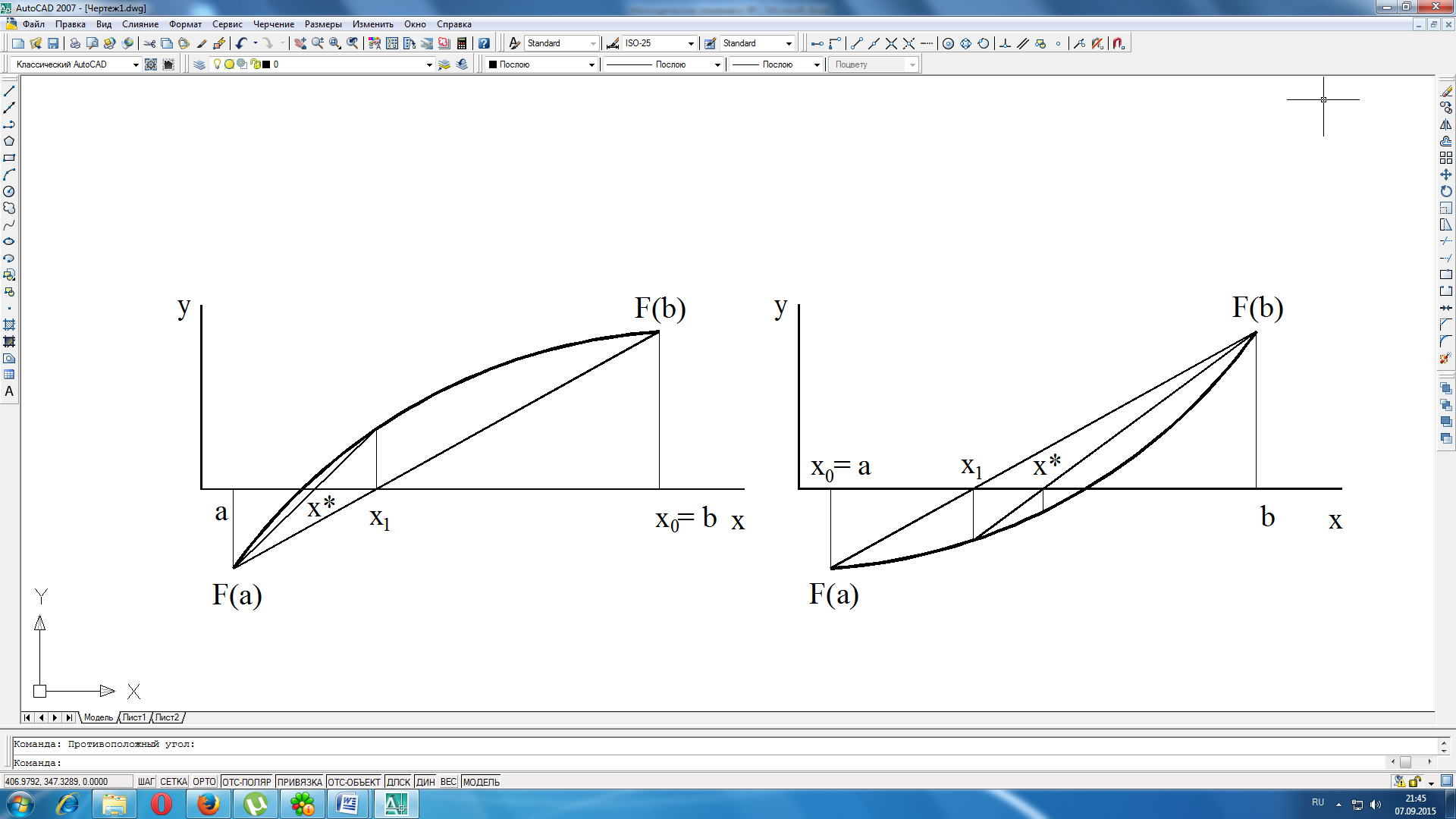
а) б)
Рисунок 1.2 Графическая интерпретация метода хорд: а) F(a)F //(a)>0 б) F(a)F //(a)<0
Пусть f(a)*f//(a)>0 (рис.2а). Тогда x0=b, точка a будет оставаться неподвижной. Следующее приближение x1 находим как точку пересечения хорды, соединяющей точки (a, f(a)) и (x0, f(x0)) с осью x.
В аналитической геометрии выводится формула, задающая уравнение прямой, проходящей через две точки с координатами (х1; у1) и (х2; у2):
Таким образом, для f(a)*f//(a)>0 точка пересечения хорды с осью x:
На следующей итерации в качестве x0 надо взять вычисленное значение x1.
Пусть теперь f(a)f //(a)<0 (рис.2б). Тогда x0=a, точка b неподвижна. Проведем хорду, соединяющую точки (b, f(b)) и (x0, f(x0)):
Вычисляем точку пересечения хорды с осью x: .
На следующей итерации в качестве x0 надо взять вычисленное значение x1
Повторять операцию следует
до тех пор, пока xi-xi-1<
не станет меньше или равно заданному
значению погрешности.
Задание к лабораторной работе №1
Таблица 1.1 – Исходные данные для выполнения самостоятельного задания
|
№ варианта |
Функция |
Интервал |
|
1 |
|
- |
|
2 |
|
[-1,0] |
|
3 |
|
- |
|
4 |
|
[0,3] |
|
5 |
|
[1,5] |
|
6 |
|
[0,3] |
|
7 |
|
[0,3] |
|
8 |
|
[1,5] |
|
9 |
|
[0,3] |
|
10 |
|
[-1,1] |
|
11 |
|
[5,10] |
|
12 |
|
[0,1] |
|
13 |
|
[0,1] |
|
14 |
|
[0,1] |
|
15 |
|
[0,10] |
|
16 |
|
[0,1] |
|
17 |
|
[0,5] |
|
18 |
|
[0,20] |
|
19 |
|
[0.5,2] |
|
20 |
|
[0.5,2] |
Вариант выполнения работы соответствует порядковому номеру в журнале проведения занятий преподавателя. Данные выбираются из табл.1.
1. Построить в среде Mathcad зависимость f(x) и локализовать корни.
2. Рассчитать корни нелинейного уравнения
вышеприведенными методами с точностью
.
Результаты расчетов занести в таблицу
результатов расчета;
Таблица результатов расчета
|
Шаг |
х |
f(x) |
Ошибка ɛ |
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
N |
|
|
|
3. Проверить результаты расчетов в среде Mathcad. Программы расчетов приведены в приложении к методическим указаниям.
Содержание отчета
Отчет по лабораторной работе должен содержать:
1. Титульный лист, оформленный согласно приложению 1;
2. Условие задания и порядок выполнения расчетов.
3. Протокол работы в виде документа Mathcad с текстовыми блоками заголовков заданий и формульных блоков их выполнения по каждому пункту заданию согласно своему варианту;
4. Выводы о проделанной работе.
Контрольные вопросы
1. Объяснить суть метода бисекций (деления отрезка пополам).
2. Объяснить суть метода метода секущих (хорд).
4. Лабораторная работа №2
ИНТЕРПОЛИРОВАНИЕ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТОВ
Целью работы является изучение методов и алгоритмов интерполирования и аппроксимации функций и реализации их в MathCad.
Содержание работы
1. Исследование локальных методов интерполирования результатов эксперимента;
2. Исследование глобальные методов интерполирования результатов эксперимента.
Перечень необходимых материалов, реактивов, приборов, оборудования
Лабораторная работа проводится в компьютерном классе с сетевым оборудованием со следующим программным обеспечением: ОС MS Windows XP и выше, офисный пакет OpenOffice, система инженерных и математических расчетов MathCad.
Методические указания
Аппроксимация - приближенное выражение сложной функции с помощью более простых.
Интерполя́ция - способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
К интерполяционным методам можно отнести: кусочно-постоянную, кусочно-линейную интерполяцию, кубический интерполяционный сплайн, интерполяционный многочлен Лагранжа.
1. Кусочно-постоянная интерполяция
На
каждом отрезке
интерполяционный
многочлен равен константе, а именно
левому или правому значению функции.
Для
левой
кусочно-линейной интерполяции
,
т.е.
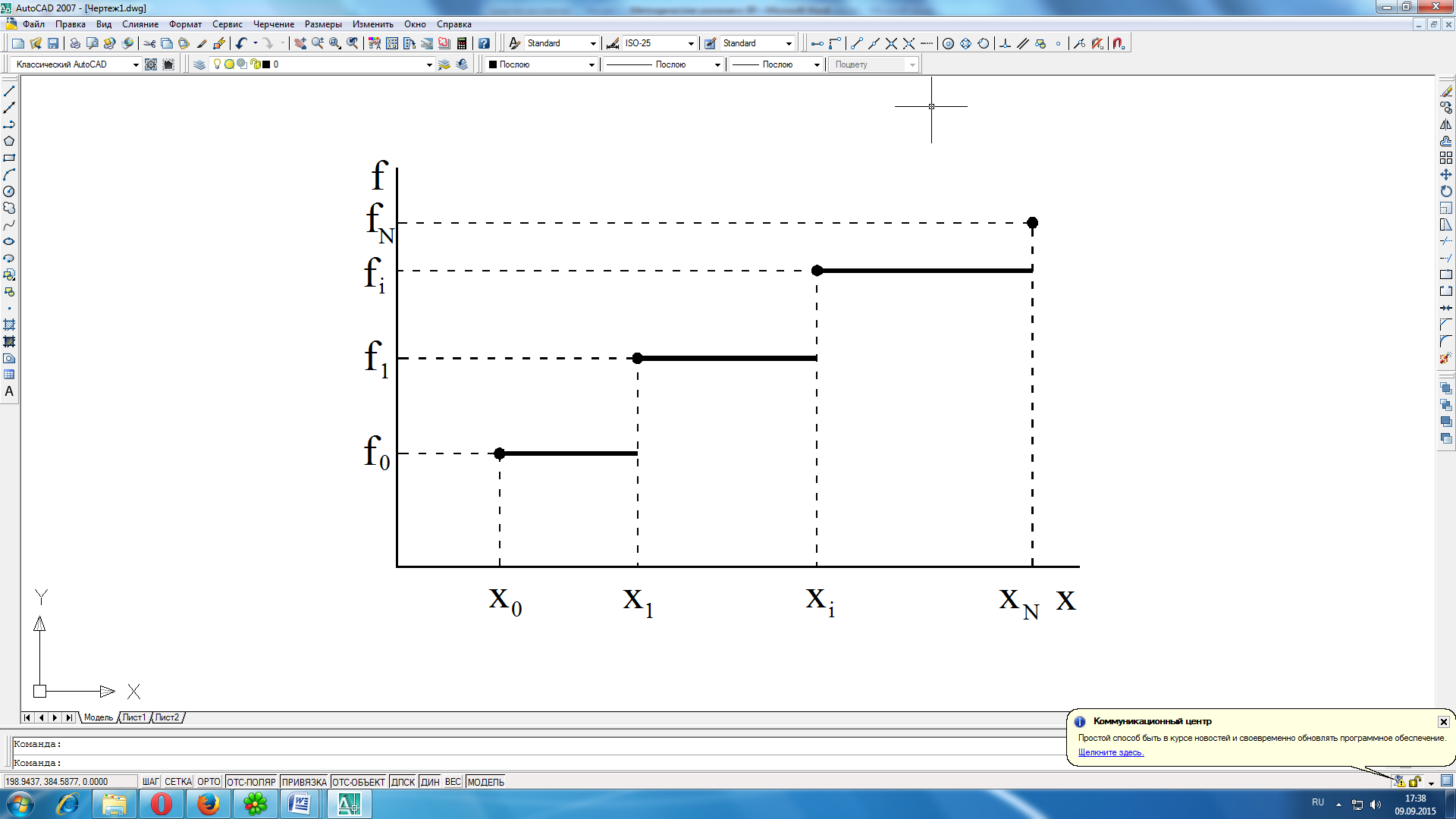
Рисунок 2.1 Левая кусочно-постоянная интерполяция
Для правой кусочно-линейной интерполяции , т.е.
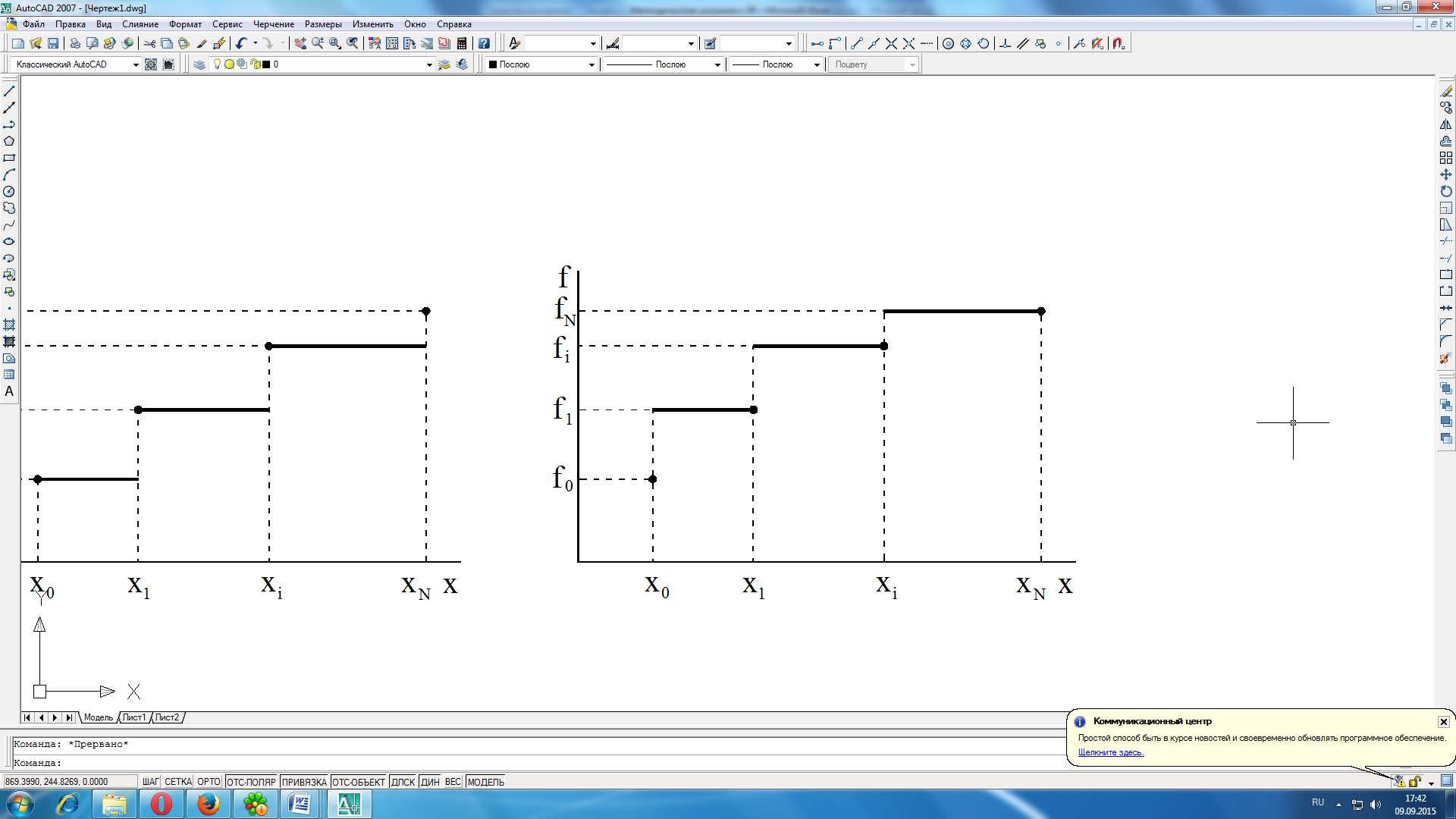
Рисунок 2.2 Правая кусочно-постоянная интерполяция
2. Кусочно-линейная интерполяция
На
каждом интервале
функция
является линейной
.
Значения коэффициентов находятся из уравнений:
Функцию
на каждом интервале можно записать в
виде:
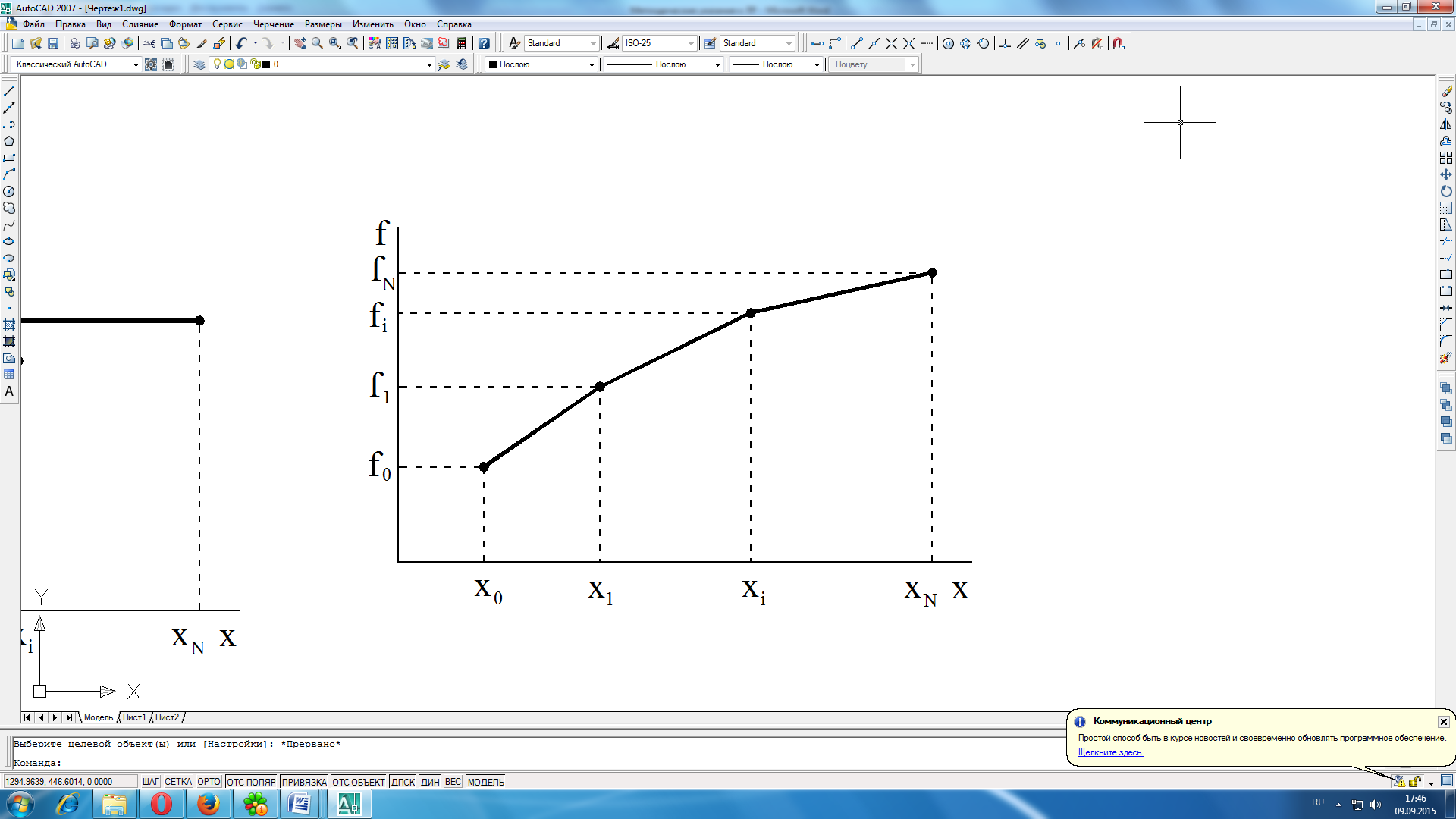
Рисунок 2.3 кусочно-линейной интерполяция
3. Интерполяционный многочлен Лагранжа
Интерполяционный многочлен Лагранжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек.
где базисные полиномы определяются по формуле:
Для трех узлов интерполяции N=2
- уравнение, проходящей через точки (x0, y0), (x1, y1), (x2, y2)
Задание к лабораторной работе №2
Таблица 2.1 – Исходные данные для выполнения самостоятельного задания
|
№ |
Функции |
Интервал |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
Вариант выполнения работы соответствует порядковому номеру в журнале проведения занятий преподавателя. Данные выбираются из табл.2.1.
Для заданной функции f(x) выполнить следующее:
1.
Разбить исходный интервал []
на 10 равных интервалов.
2. Записать уравнения для кусочно-постоянной интерполяции (левой и правой). Изобразить графически интерполирующие и заданную функцию. Используя Mathcad, определить интегральную ошибку интерполирования.
3. Повторить пункты 2-4 для кусочно-линейной интерполяции.
4. Записать уравнения многочлена Лагранжа для степеней от 2 до 5. Применив MatCad изобразить графически интерполирующие функции. Определить интегральные ошибки.
Содержание отчета
Отчет по лабораторной работе должен содержать:
1. Титульный лист, оформленный согласно приложению 1;
2. Условие задания и порядок выполнения расчетов.
3. Протокол работы в виде документа Mathcad с текстовыми блоками заголовков заданий и формульных блоков их выполнения по каждому пункту заданию согласно своему варианту;
4. Выводы о проделанной работе.
Контрольные вопросы
1. Что называется интерполяцией и аппроксимацией функции? Чем отличается локальная интерполяция от глобальной?
2. Объяснить суть метода кусточно-постоянной и кусочно -линейной интерполяций.
3. Объяснить методику определения коэффициентов уравнений кусочно -линейной интерполяций. От чего зависит точность интерполирования?
4. Какие условия накладываются на сплайн-функцию?
5. Из каких уравнений определяются коэффициенты сплайн-функции?
6. Объяснить методику получения многочлена Лагранжа. Как зависит точность интерполяции от количества узлов?
5. Лабораторная работа №3
МОДЕЛИРОВАНИЕ ЭЛЕКТРИЧЕСКИХ НАГРУЗОК
Целью работы является изучение методов и алгоритмов моделирования статических характеристик электрических нагрузок в системах электроснабжения.
Содержание работы
1. Математическое моделирование статических нагрузок по напряжению методом полиноминальной интерполяции.
Перечень необходимых материалов, приборов, оборудования
Лабораторная работа проводится в компьютерном классе с сетевым оборудованием со следующим программным обеспечением: ОС MS Windows XP и выше, офисный пакет OpenOffice, система инженерных и математических расчетов MathCad.
Методические указания
В общем случае статические характеристики нагрузки по напряжению могут быть представлены в виде интерполяционных полиномов второго порядка: