Файл: Метоодические указания к ЛР.docx

4. Выводы о проделанной работе.

Контрольные вопросы

1. Объяснить суть решения дифференциального уравнения методом Эйлера.

2. Объяснить суть решения дифференциального уравнения усовершенствованный методом Эйлера .

3. Объяснить суть решения дифференциального уравнения модифицированным методом Эйлера-Коши.

4. Объяснить суть решения дифференциального уравнения методом Рунге-Кутты .

7. Лабораторная работа №5

РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Целью работы исследовать методики решения систем линейных алгебраических уравнений (СЛАУ) в интегрированной среде MathCad

Содержание работы

1. Исследовать матричный метод (метод Крамера) решения СЛУ;

2. Исследовать метод Гаусса;

3. Исследовать метод простой итерации (метод Якоби);

Перечень необходимых материалов, реактивов, приборов, оборудования

Лабораторная работа проводится в компьютерном классе с сетевым оборудованием со следующим программным обеспечением: ОС MS Windows XP и выше, офисный пакет OpenOffice, система инженерных и математических расчетов MathCad.

Методические указания

1. Матричный метод (метод Крамера)

Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как

(7.1)

Эту систему уравнений можно записать также в матричном виде:

(7.2)

где

A – матрица системы, – вектор правых частей, – вектор неизвестных.

При известных A и требуется найти такие , при подстановке которых в систему уравнений она превращается в тождество.

Необходимым и достаточным условием существования единственного решения СЛАУ является условие det A≠0, т.е. определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.

При небольшой размерности системы m (m = 2,…,5) на практике часто используют формулы Крамера для решения СЛАУ:

2. Метод Гаусса

Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений

(7.3)

первый элемент . Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на и исключим из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при в соответствующей строке. Получим

(7.4)

Если , то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей

(7.5)

Из нее в обратном порядке находим все значения

(7.6)

Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных – обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому предварительно необходимо выбирать главный элемент путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных так, чтобы выполнялось условие:

---

т.е. осуществляется выбор первого главного элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a₁₁ был максимальным по модулю. Разделив первую строку на главный элемент, как и прежде, исключают x₁ из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.

3. Метод простой итерации (метод Якоби)

Пусть требуется решить систему линейных уравнений, которая в матричном виде записывается как:

,

где

(7.7)

Предположим, что диагональные элементы матриц A исходной системы не равны 0 (a_ii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно x₁, второе относительно x₂ и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:

(7.8)

Теперь, задав нулевое приближение , по рекуррентным соотношениям (5.8) можем выполнять итерационный процесс, а именно:

(7.9)

Аналогично находятся следующие приближения , где в (5.9) вместо необходимо подставить .

Условие окончания итерационного процесса

(7.10)

Достаточное условие сходимости.

Если выполнено условие диагонального преобладания, т.е. ,

то итерационный процесс сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.

Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут

(7.11)

или .

Задание к лабораторной работе №5

Таблица 7.1 – Исходные данные для выполнения самостоятельного задания

№ В	Система линейных уравнений	№ В	Система линейных уравнений
1		13
2		14
3		15
4		16
5		17
6		18
7		19
8		20
9		21
10		22
11		23
12		24

Решить систему линейных уравнений:

1. Решить СЛАУ матричным методом и сравнить результаты с расчетом в среде Mathcad;

2. Решить СЛАУ методом Гаусса;

3. Решить СЛАУ методом простой итерации;

4. Решить СЛАУ методом Зейделя.

Содержание отчета

Отчет по лабораторной работе должен содержать:

1. Титульный лист, оформленный согласно приложению 1;

2. Условие задания и порядок выполнения расчетов.

3. Протокол работы в виде документа Mathcad с текстовыми блоками заголовков заданий и формульных блоков их выполнения по каждому пункту заданию согласно своему варианту;

4. Выводы о проделанной работе.

Контрольные вопросы

1. Объяснить суть метода решения СЛАУ метод Крамера;

2. Объяснить суть метода решения СЛАУ методом Гаусса;

3. Объяснить суть метода простой итерации. Условия сходимости метода;

---

4. Объяснить суть метода Зейделя. Условия сходимости метода.

8. Лабораторная работа №6

ТОПОЛОГИЧЕСКИЕ МЕТОДЫ АНАЛИЗА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Целью работы является исследование установившихся рабочих режимов сложных схем замещения электрических цепей на базе применения аппарата матриц и элементов топологической теории графов.

Содержание работы

1. Исследование установившегося режима цепи методом контурных токов;

2. Исследование установившегося режима цепи методом узловых напряжений.

Перечень необходимых материалов, приборов, оборудования

Лабораторная работа проводится в компьютерном классе с сетевым оборудованием со следующим программным обеспечением: ОС MS Windows XP и выше, офисный пакет OpenOffice, система инженерных и математических расчетов MathCad.

Методические указания

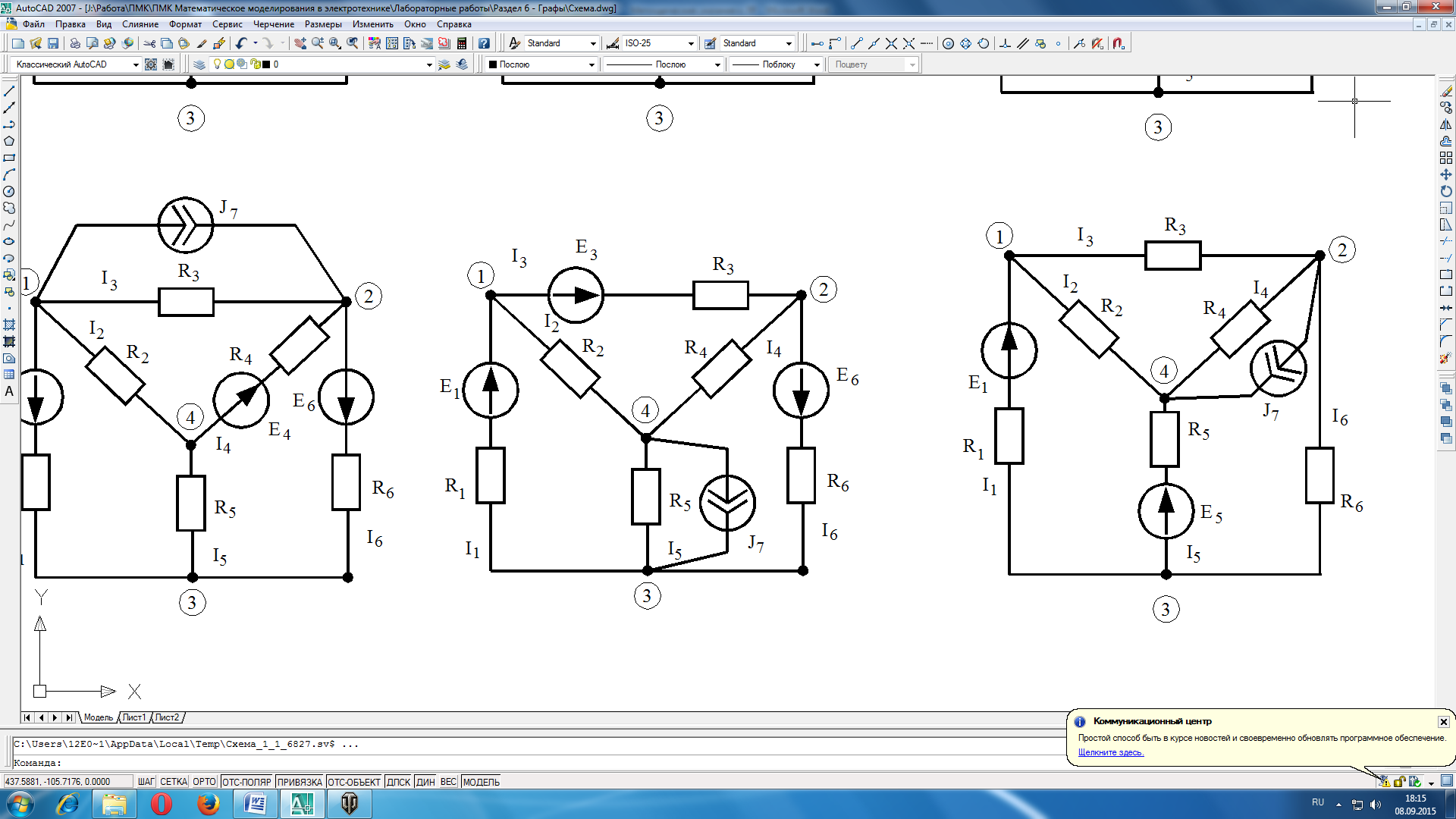
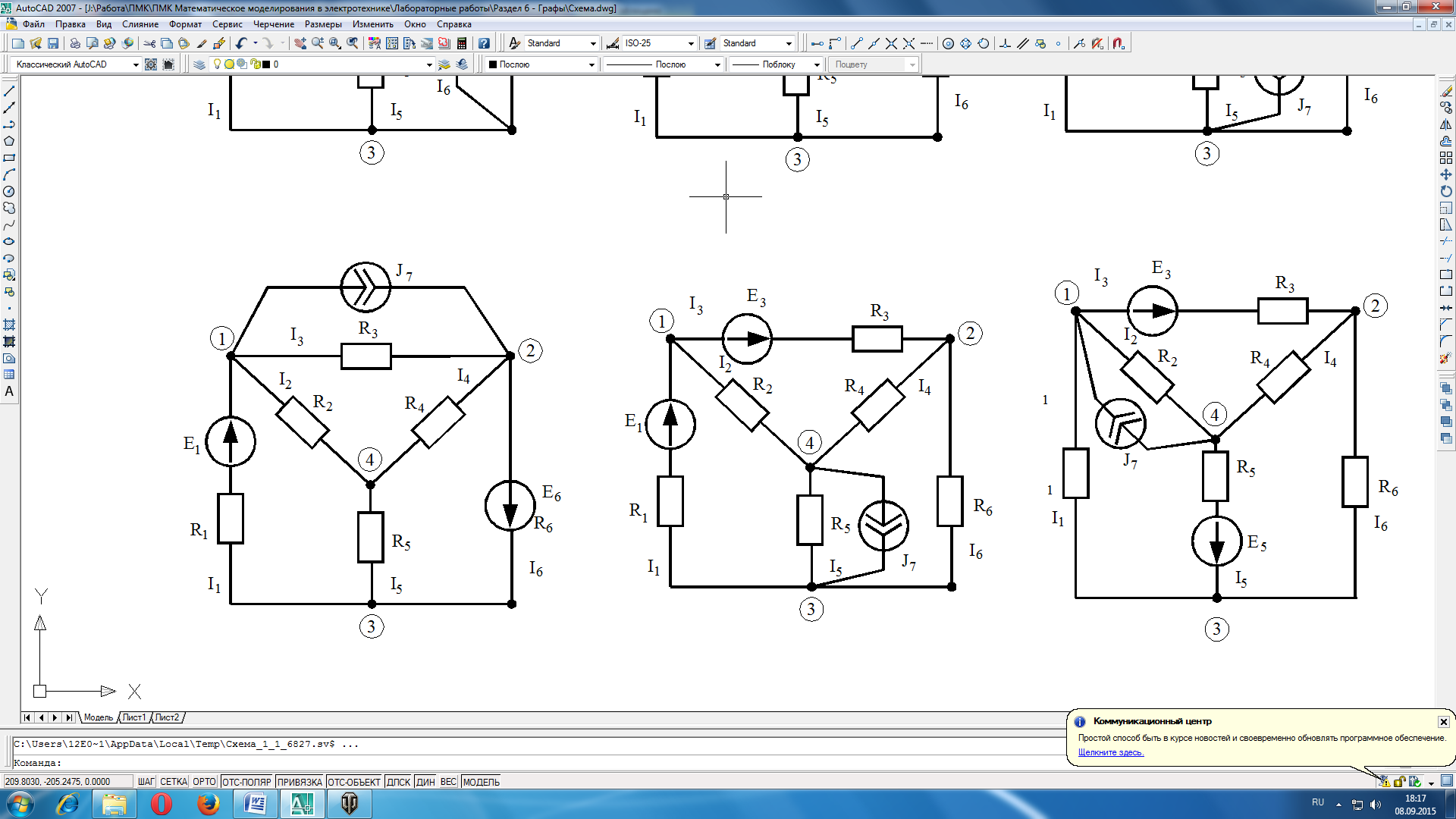
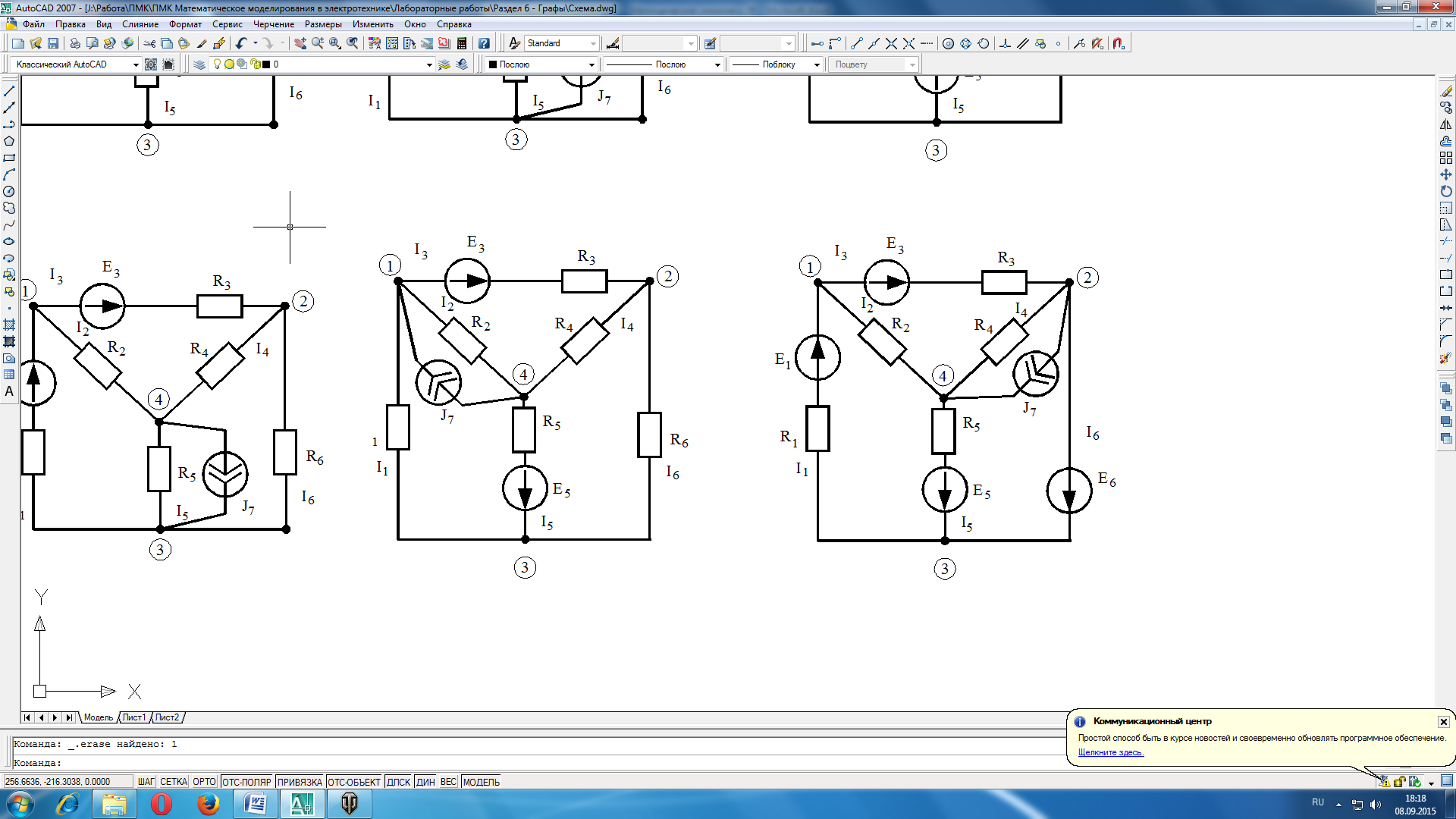
Режим любой электрической цепи, например изображенной на рис.8.1, однозначно определяется законами Кирхгофа. Вид уравнений электрического состояния цепи, зависит только от схемы соединения ветвей, т.е. от топологической структуры цепи, и не зависит от вида параметров самих элементов. В таком случае, ветви, содержащие различные двухполюсные элементы, можно представлять просто линиями, а структуру цепи - совокупностью этих линий, которая называется графом электрической цепи (рис.8.2). Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой.

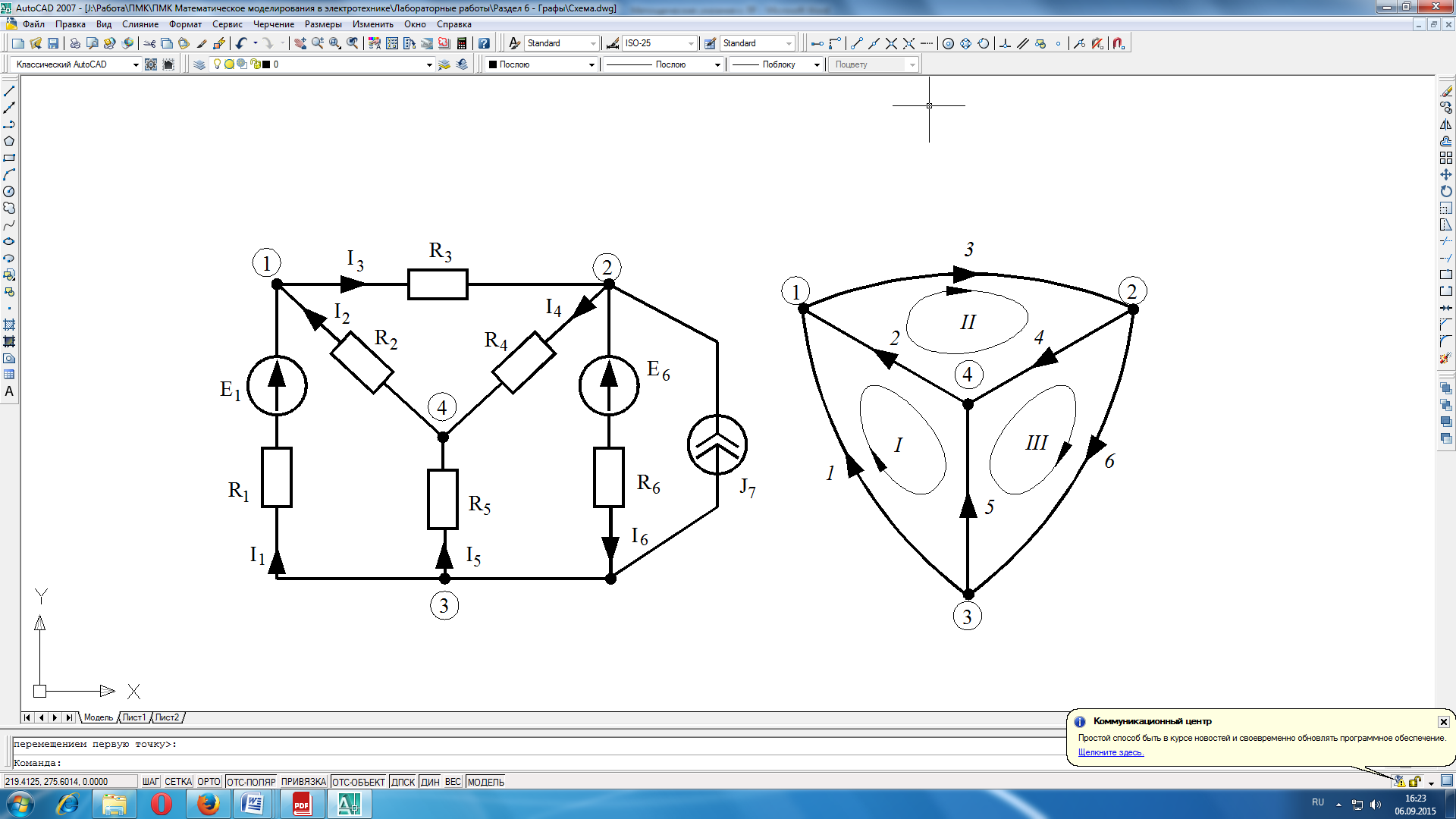
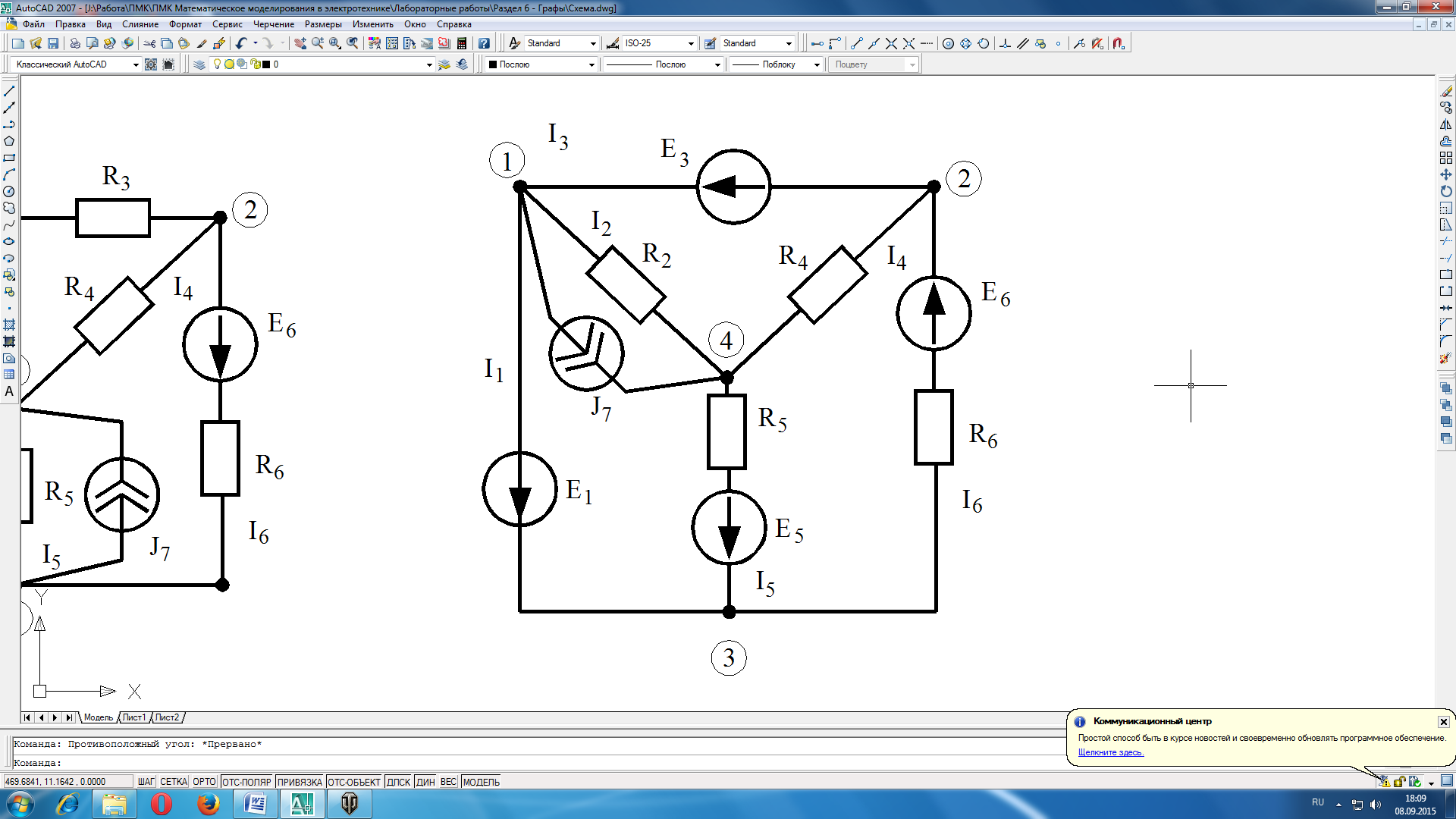
Рисунок 8.1 Электрическая схема

Рисунок 8.2 Граф электрической цепи

Подграфом графа называется часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.

В теории электрических цепей важное значение имеют следующие подграфы:

Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. Например, в схеме на рис. 6.2 ветви 3-6; 2-5; 3-4-5; 1 образуют пути между одной и той же парой узлов 1 и3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно.

Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Если между любой парой узлов графа существует связь, то граф называют связным.

Дерево – это связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа на рис. 8.2 могут служить фигуры на рис. 6.3.

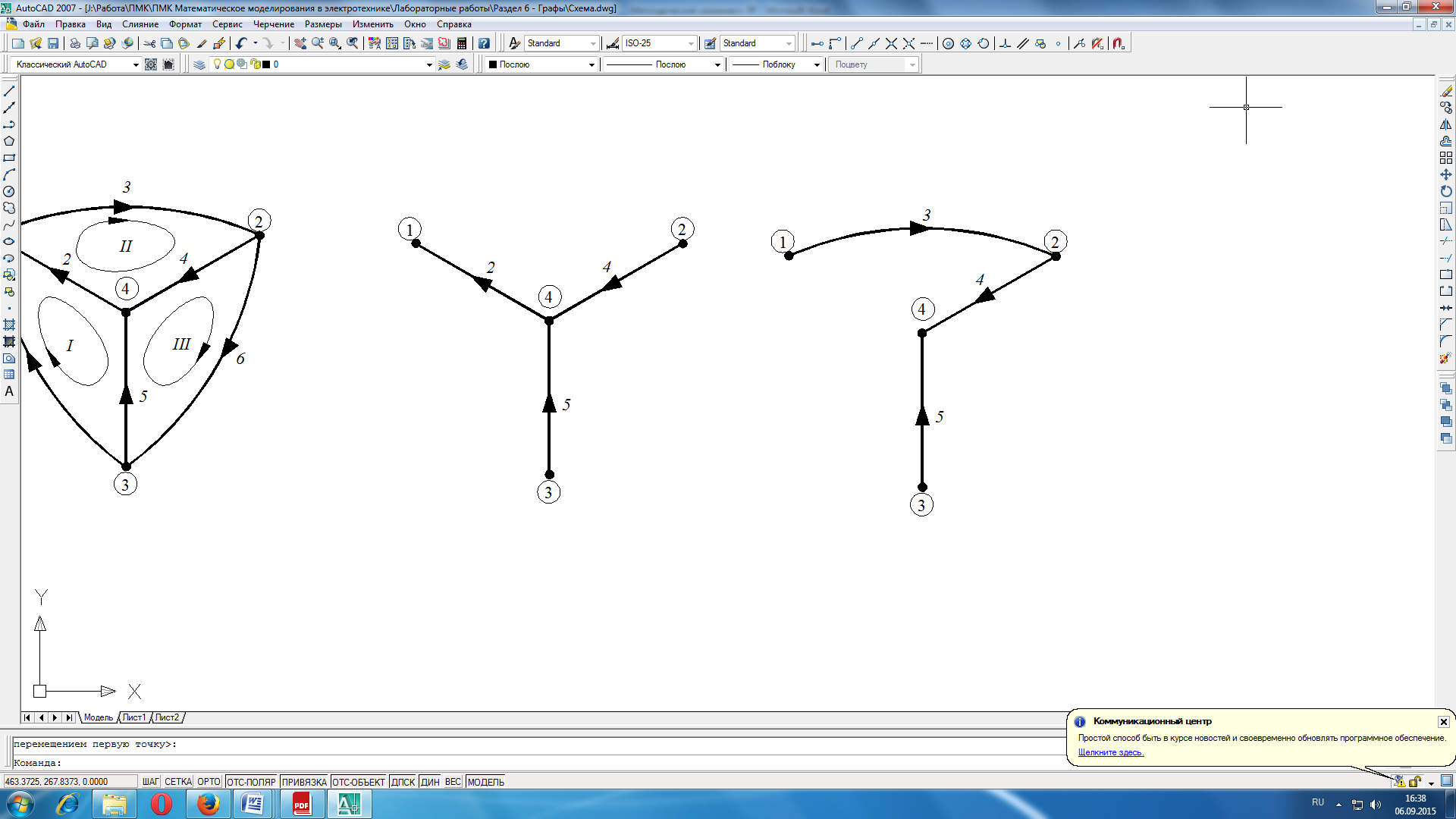
Рисунок 8.3 Примеры деревьев графа

Для аналитического описания структуры электрических цепей применяют топологические матрицы: соединений (узловая) [A] и контуров [В].

Матрица соединений, ее размерность: число строк = число узлов - 1; число столбцов = число ветвей. Матрица состоит из элементов: 1, -1, 0. Если ток ветви подходит к данному узлу то 1, если отходит то -1, если ветви нет то 0.

---

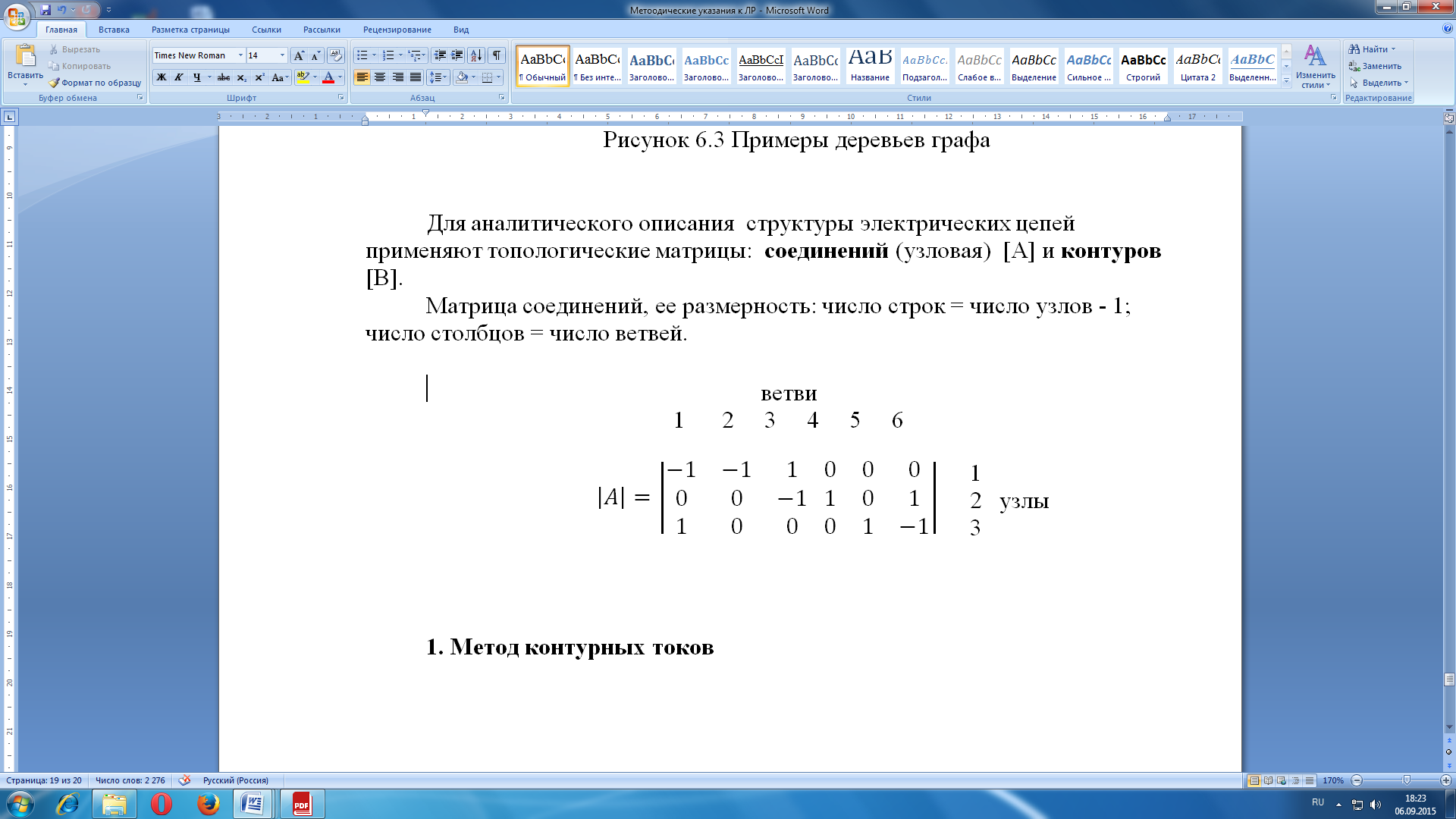
Матрица главных контуров, ее размерность: число строк = число контуров - 1; число столбцов = число ветвей. Каждая ветвь должна входить только в один контур. Если ветвь входит в контур и ее направление совпадает с обходом контура то 1, не совпадает -1, ветви нет в контуре 0.

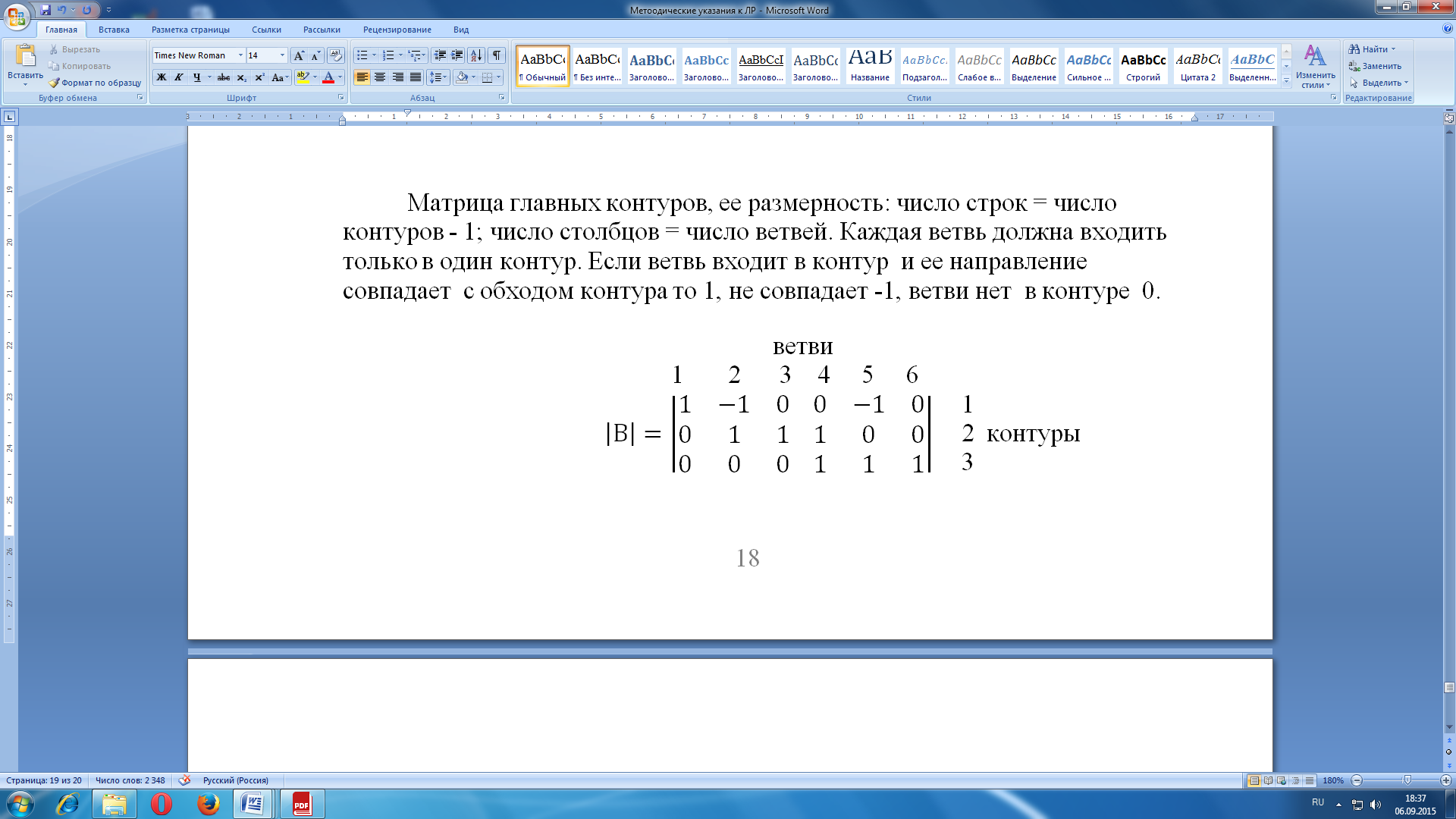
Отметим, что для матриц А, В, составленных для одного и того же графа, должно выполнятся соотношение

(8.1)

Матрицы исходных данных и исходных токов

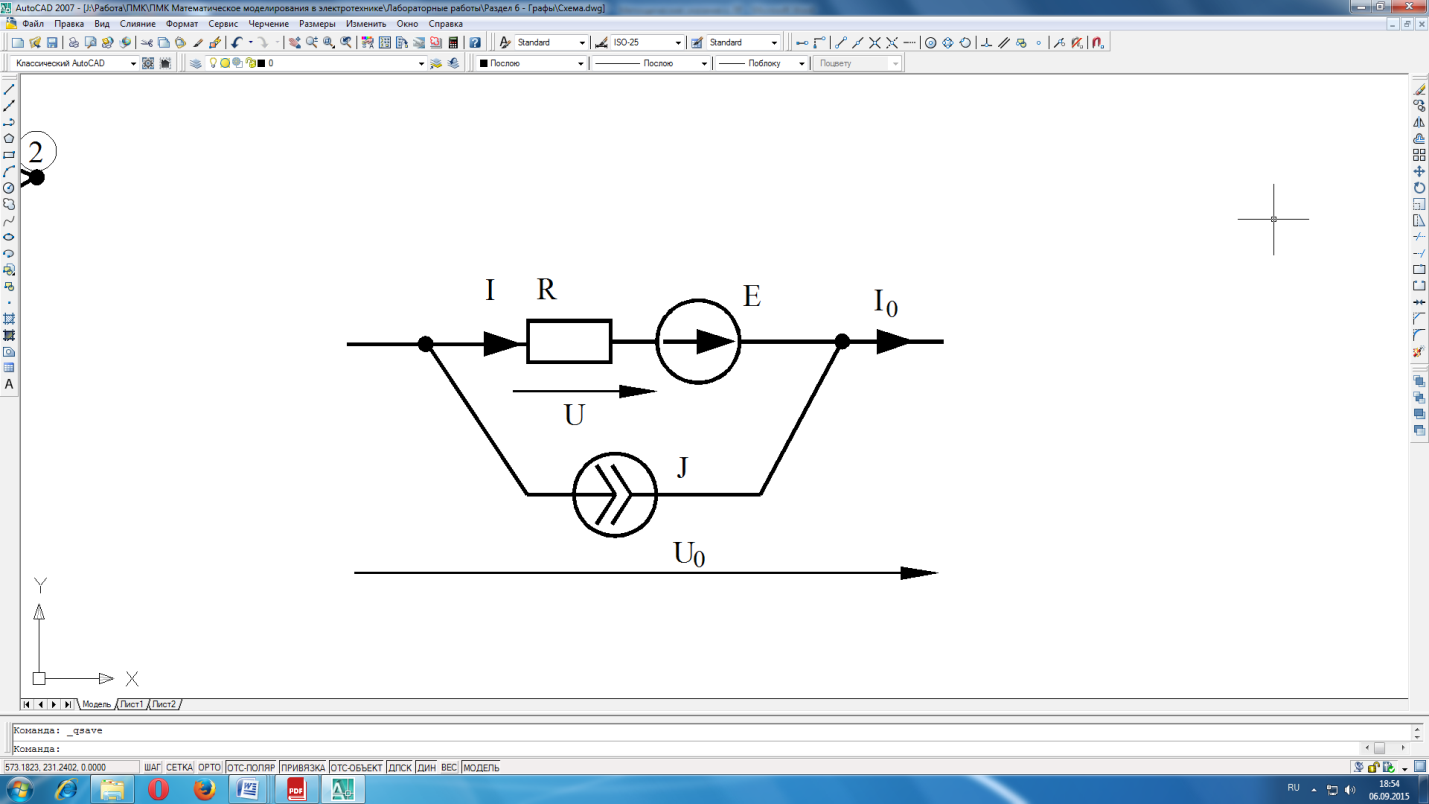
Рисунок 8.4 Обобщенная ветвь с источниками ЭДС и тока

(8.2)

Размерности матриц источников тока, ЭДС, сопротивлений и искомых токов определяются количеством ветвей

; ;

[вх1] [вх1] [вхв] [вх1]

Закон Ома в матричной форме

Для обобщенной ветви представленной на рис.6.4 получим

.

Это соотношение в матричной форме для всех ветвей схемы

. (8.3)

Первый закон Кирхгофа в матричной форме

Очевидно, что умножив матрицу соединений на матрицу искомых токов мы получим I закон Кирхгофа: так как , то

(8.4)

Второй закон Кирхгофа в матричной форме

Если обе части уравнения закона Ома умножить на матрицу главных контуров и учесть , что

. (8.5)

Метод контурных токов

В качестве независимых переменных (контурных токов) принимают токи ветвей связи. Для рассматриваемого примера ветви связи : 1-2 с током I₃; 2-3 с током I₆; 1-3 с током I₁. Если транспонировать матрицу контуров и умножить на матрицу контурных токов то получим матрицу обобщенных токов ветвей I₀.

. (8.6)

где : - транспонированная матрица контуров;

- столбец матрица контурных токов.

Из уравнения II закона Кирхгофа (6.5) с учетом (6.6) получим

откуда выразим контурный ток

(8.7)

Метод узловых потенциалов

Матрица узловых потенциалов:

(8.8)

где - диагональная матрица проводимостей.

Матрица токов ветвей

(8.9)

Напряжения ветвей

(8.10)

Задание к лабораторной работе №6

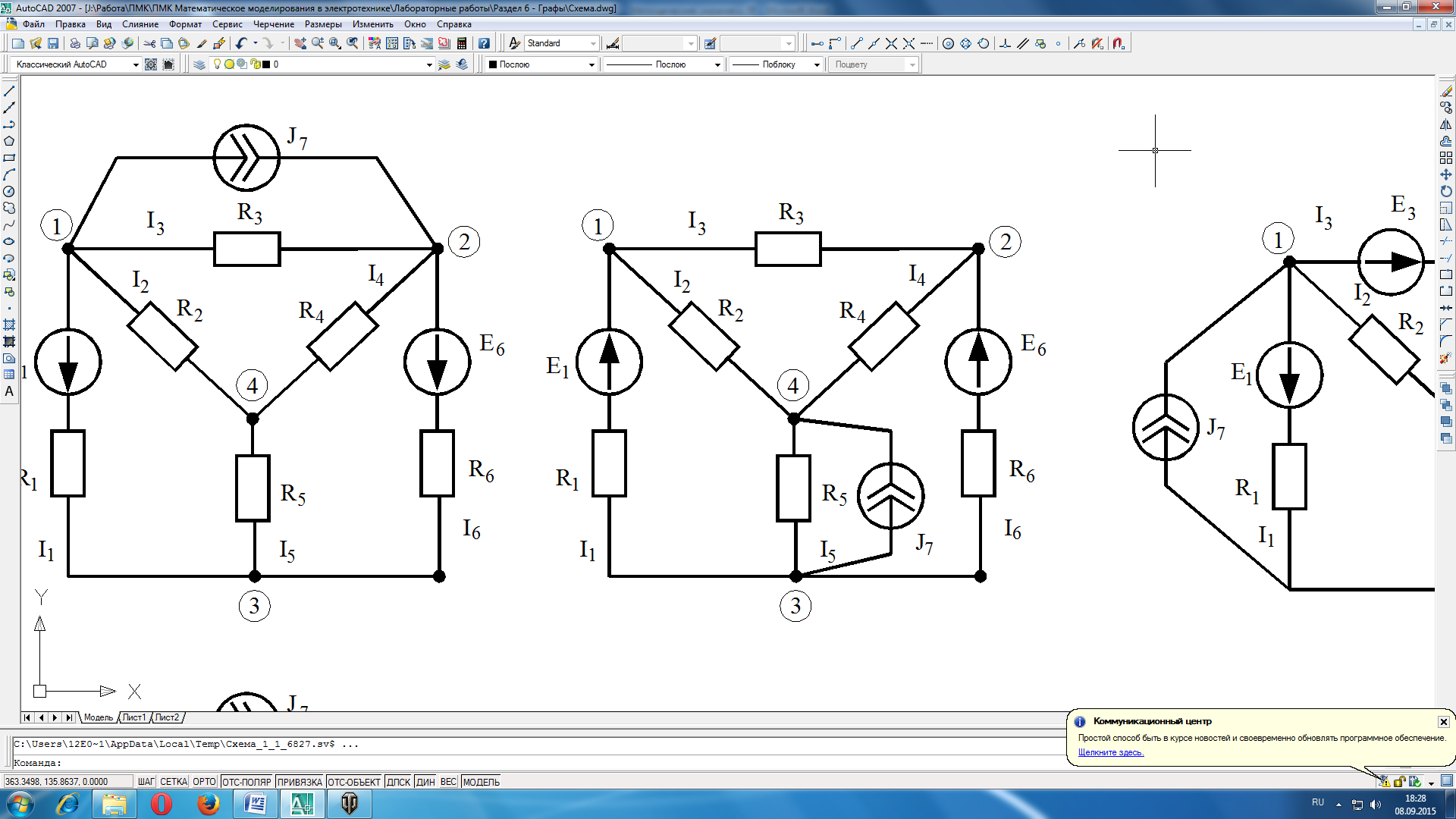
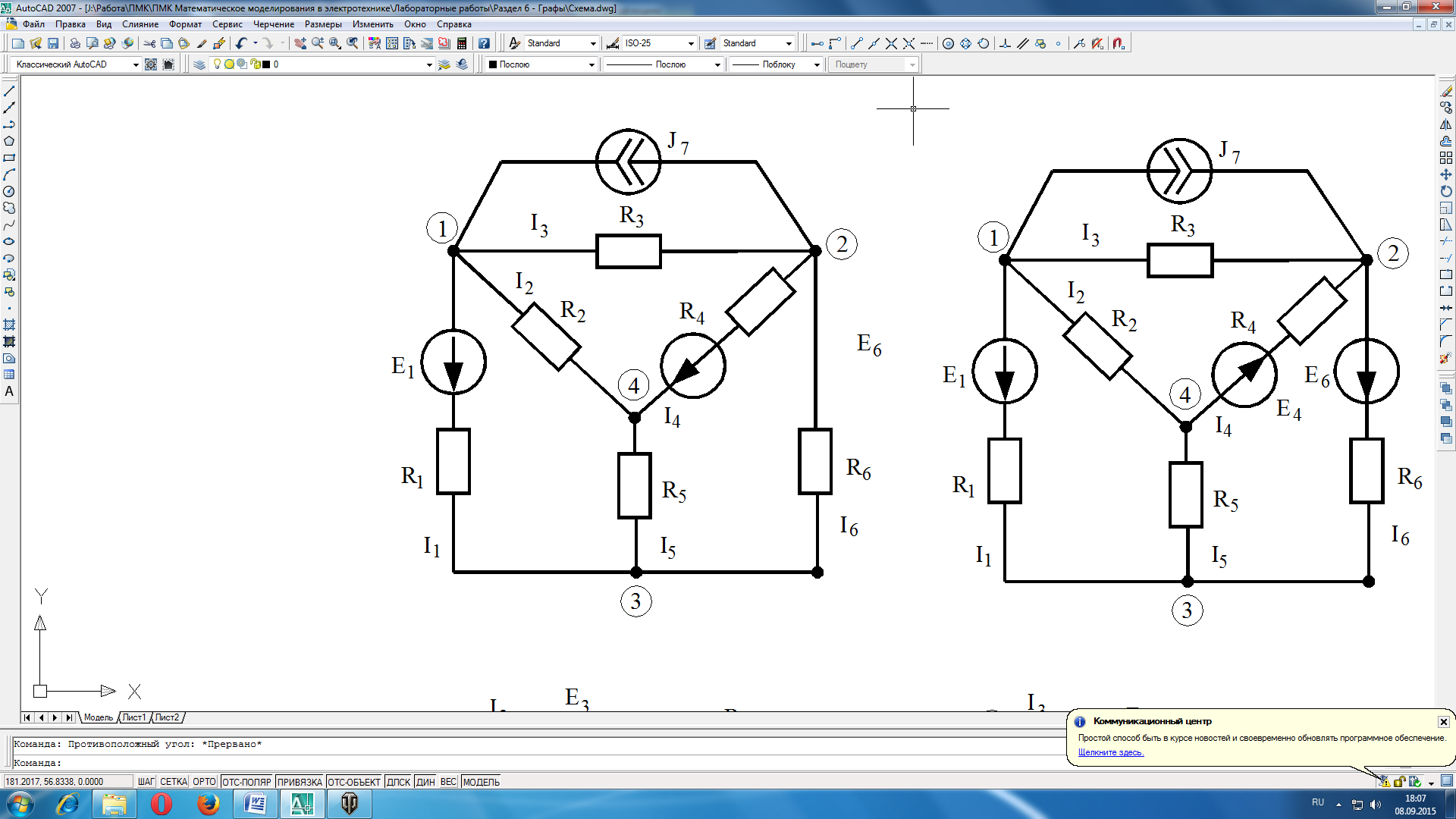
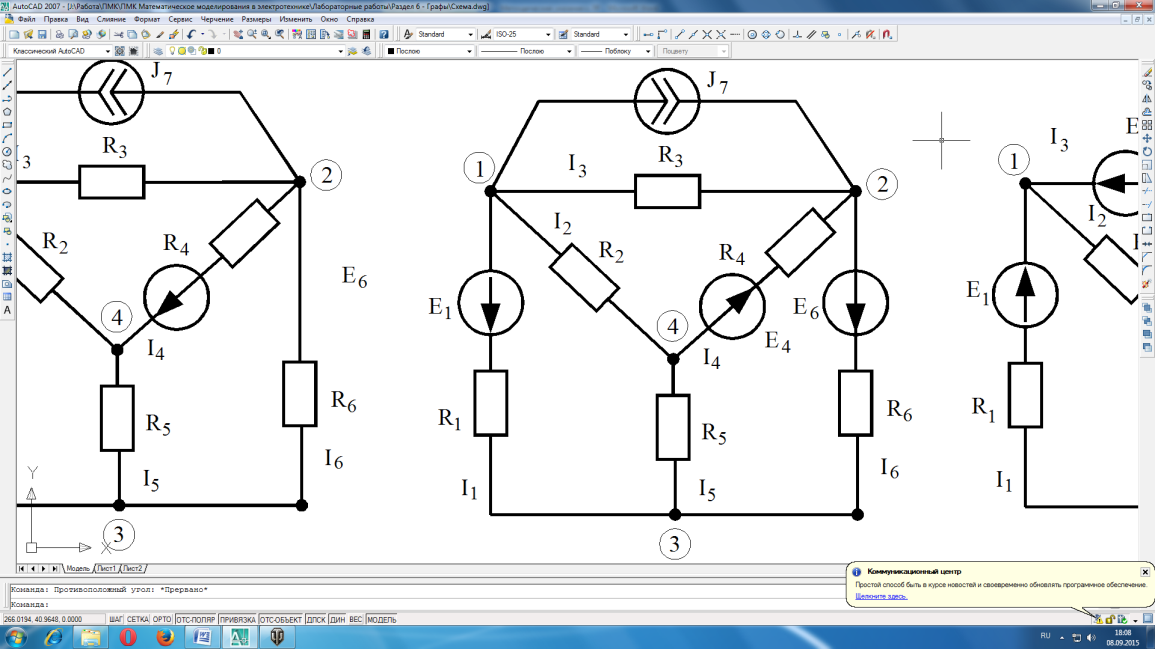
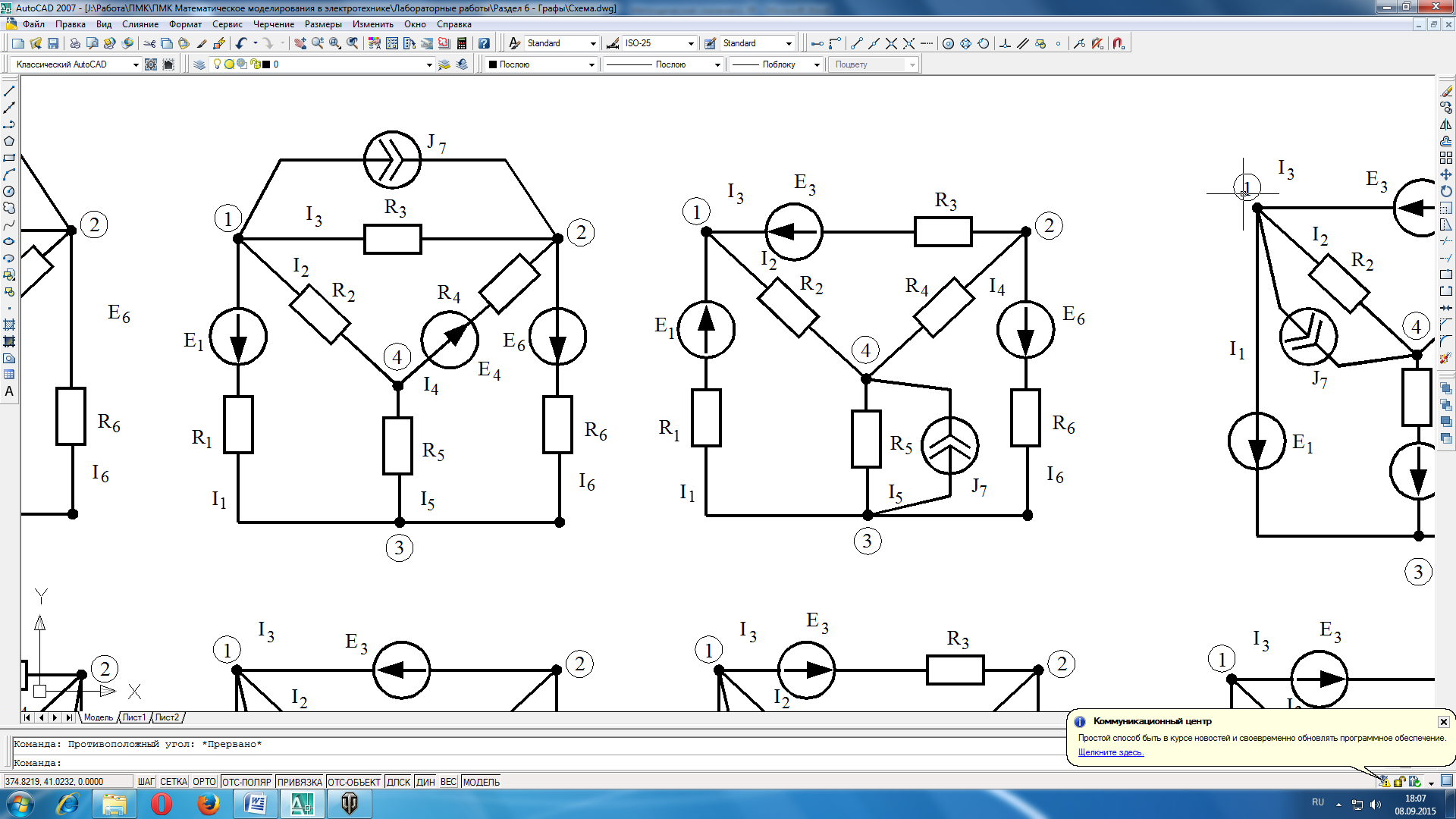
В соответствии с вариантом задания выполнить расчет электрической цепи методами контурных токов и узловых напряжений. Выполнить проверку решения путем составления баланса мощностей. Вариант схемы выбирается по журналу преподавателя.

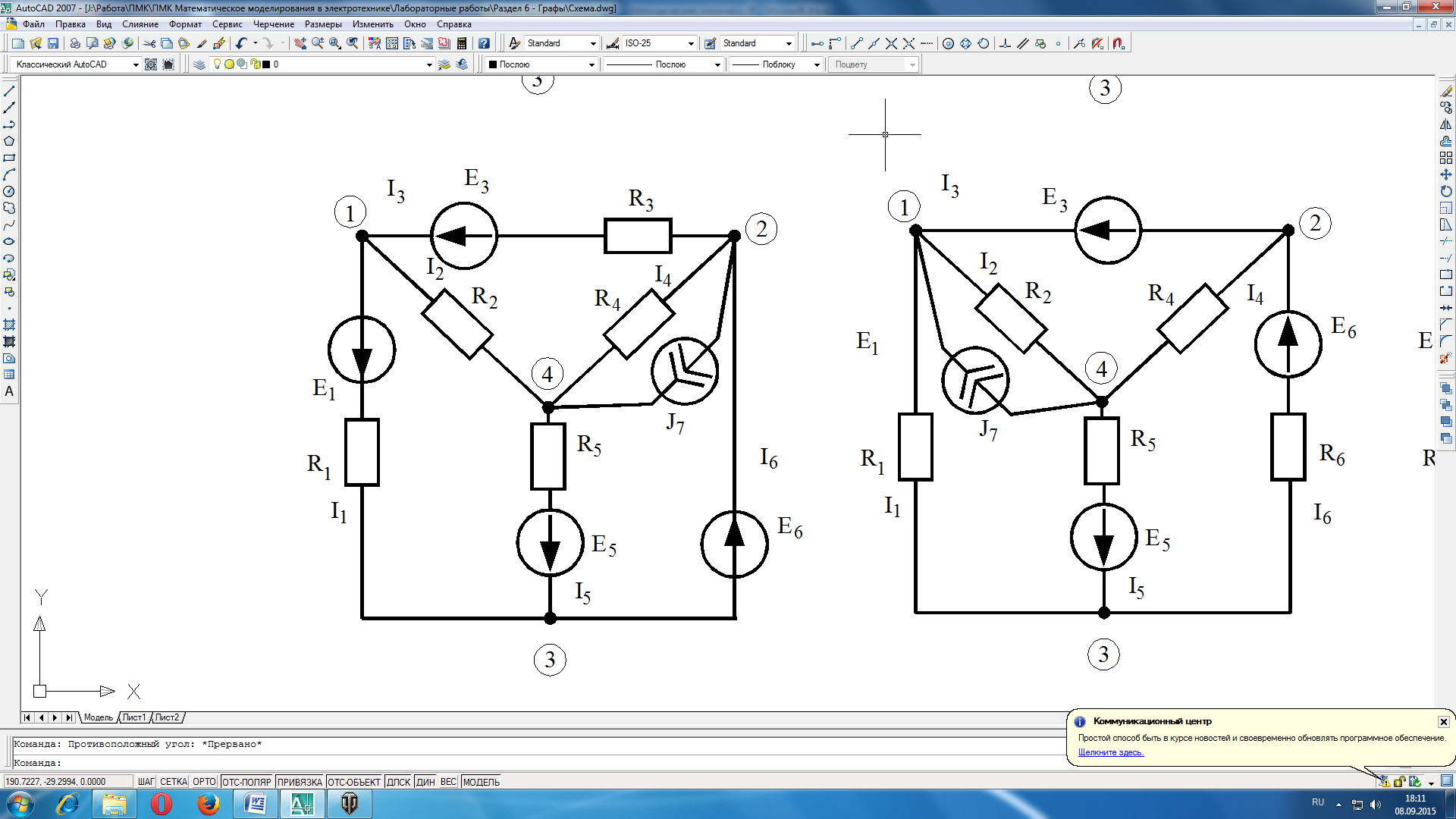
Вариант 1	Вариант 2
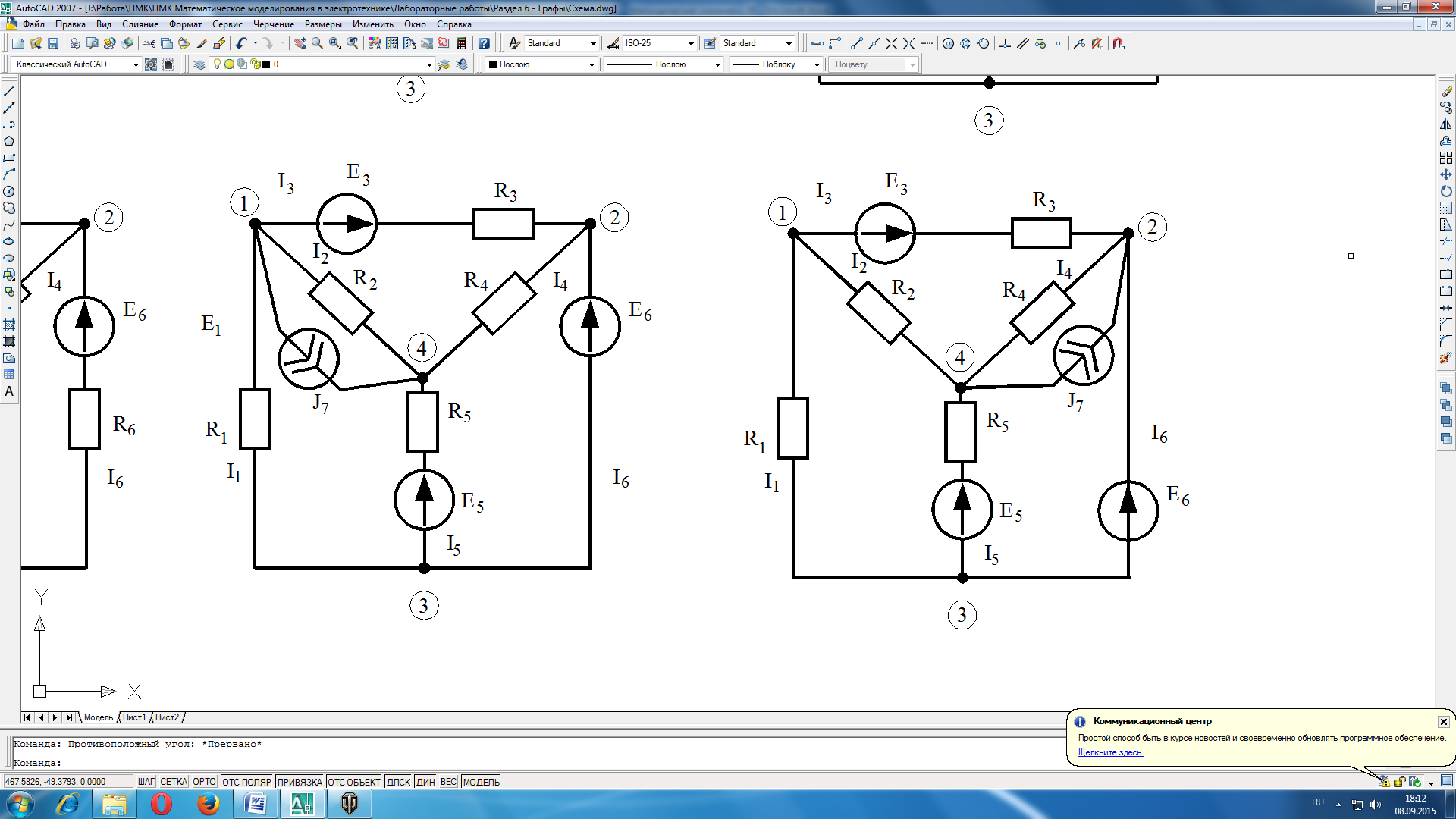
Вариант 3	Вариант 4
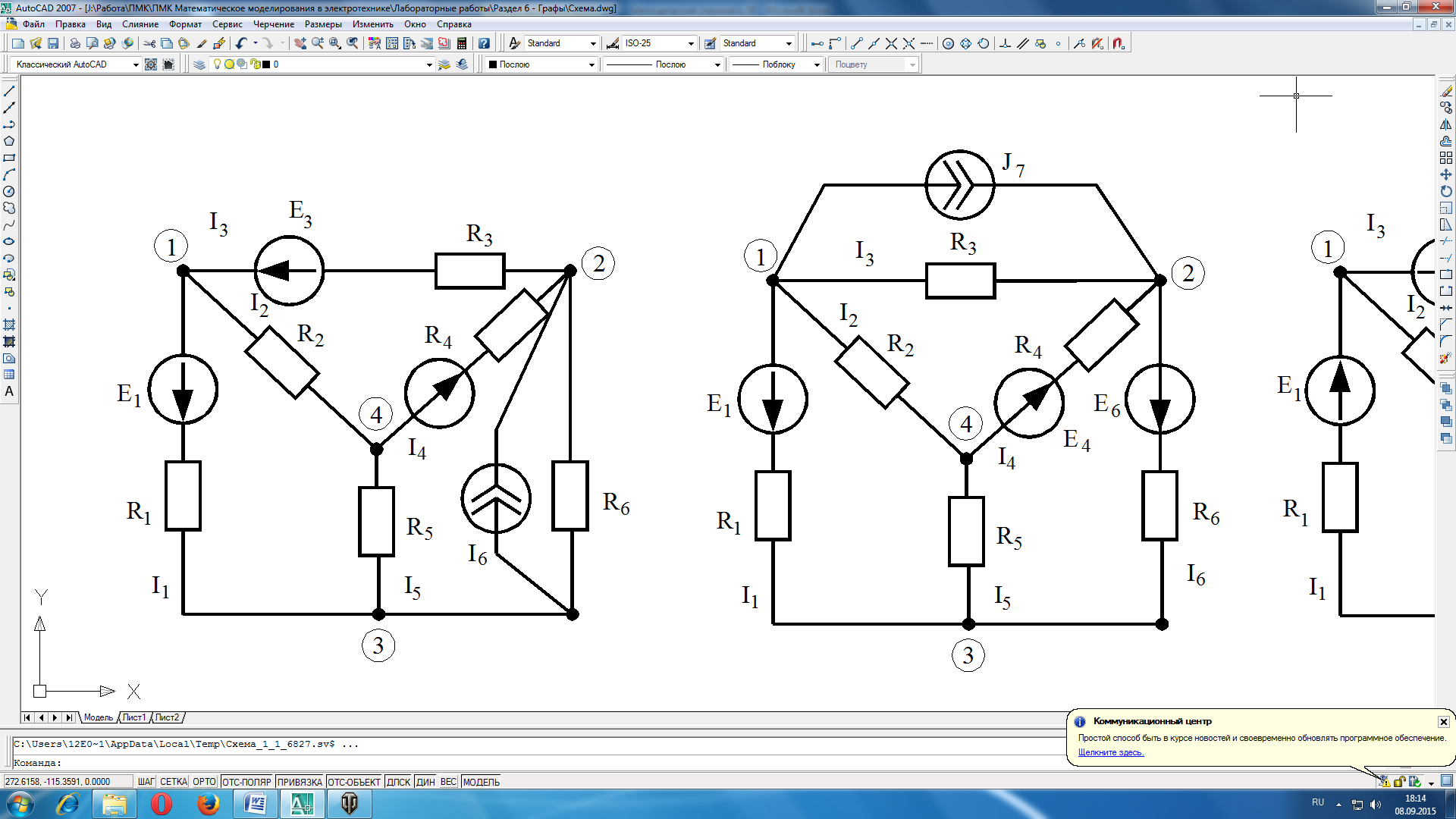
Вариант 5	Вариант 6
Вариант 7	Вариант 8
Вариант 9	Вариант 10
Вариант 11	Вариант 12
Вариант 13	Вариант 14
Вариант 15	Вариант 16
Вариант 17	Вариант 18
Вариант 19	Вариант 20

Таблица 8.1 Параметры схемы

Е1

Е2

Е3

Е4

Е5

Е6

R1

R2

R3

R4

R5

R6

J6

В

В

В

В

В

В

Ом

Ом

Ом

Ом

Ом

Ом

А

10

20

30

15

25

35

10

15

12

25

30

15

5

---

Содержание отчета

Отчет по лабораторной работе должен содержать:

1. Титульный лист, оформленный согласно приложению 1;

2. Условие задания и порядок выполнения расчетов.

3. Протокол работы в виде документа Mathcad с текстовыми блоками заголовков заданий и формульных блоков их выполнения по каждому пункту заданию согласно своему варианту;

4. Выводы о проделанной работе.

Контрольные вопросы

1. Сформулируйте основные топологические понятия для электрических цепей.

2. Как составляется узловая матрица?

3. Как составляется такое контурная матрица?

4. Как выполняется расчет электрической цепи методом контурных токов?

5. Как выполняется расчет электрической цепи методом узловых напряжений?

6. Как выполнить расчет баланса мощности?

9. Лабораторная работа №7

АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ С ИСПОЛЬЗОВАНИЕМ Mathcad

Целью работы является исследование переходного процесса в цепях постоянного тока операторным методом с применением ЭВМ.

Содержание работы

1. Исследование переходного процесса в цепи постоянного тока операторным методом . с использованием Mathcad.

Перечень необходимых материалов, приборов, оборудования

Лабораторная работа проводится в компьютерном классе с сетевым оборудованием со следующим программным обеспечением: ОС MS Windows XP и выше, офисный пакет OpenOffice, система инженерных и математических расчетов MathCad.

Методические указания

Сущность операторного метода заключается в том, что решение задачи анализа цепи переносится из области функций действительного переменного t в область функций комплексного переменного p = σ + jω. В результате система интегро-дифференциальных уравнений переменной t заменяется системой алгебраических уравнений комплексной переменной p. Далее по полученному результату решения алгебраических уравнений выполняется обратный переход в область функций действительного переменного. Базируется операторный метод на преобразованиях Лапласа.

Из курса математического анализа известно, что если f(t) имеет ограниченный рост, то интеграл

сходится абсолютно и является аналитической функцией комплексного переменного p = σ + jω.

Интегральное уравнение (7.1) является прямым преобразованием Лапласа; функция f(t) называется оригиналом , а F(p) – изображением по Лапласу.

Таблица 9.1 Изображения типовых функций

f(t)
F(p)

Для нахождения изображения функции в среде Mathcad используется команда "laplace", расположенная в символьной панели инструментов.

Формат записи команды: . Заметим, что для программы Mathcad оператор записывается буквой s, а не p!

Для нахождения неизвестных величин операторным методом можно пользоваться известными электротехническими законами и методиками: законы Ома, Кирхгофа, метод контурных токов, узловых напряжений и т.д. Для составления уравнений в операторном виде первоначально электрическую схему преобразовывают к операторной форме с учетом следующих изображений:

---