Добавлен: 23.10.2018
Просмотров: 6342
Скачиваний: 71
СОДЕРЖАНИЕ
Контрольная работа № 1. Высказывания и логические операции над ними.
Задания для контрольной работы № 1.
Контрольная работа № 2. Равносильные формулы алгебры логики.
Задания для контрольной работы № 2.
Контрольная работа № 3. Совершенные нормальные формы.
Задания для контрольной работы № 3.
Контрольная работа № 4. Приложение алгебры высказываний к релейно-контактным схемам (РКС).
О
Контрольная работа № 1. Высказывания и логические операции над ними. 2
Задания для контрольной работы № 1. 3
Контрольная работа № 2. Равносильные формулы алгебры логики. 7
Задания для контрольной работы № 2. 8
Контрольная работа № 3. Совершенные нормальные формы. 11
Задания для контрольной работы № 3. 15
Контрольная работа № 4. Приложение алгебры высказываний к релейно-контактным схемам (РКС). 17
Задания для контрольной работы № 4. 19
Литература 26
Контрольная работа № 1. Высказывания и логические операции над ними.
Понятие высказывание является основным неопределяемым понятием математической логики. Под высказыванием понимают любое повествовательное предложение, о котором можно сказать истинно оно или ложно в данных условиях места и времени. Логическое значение высказывания «истина» («ложь») обозначается или буквой и, (л) или цифрой 1, (0). Высказывания обычно обозначают малыми латинскими буквами.
Отрицанием
высказывания а
называется высказывание
![]() ,
которое истинно, если а
ложно, и
ложно, если а
истинно.
Высказывание
,
которое истинно, если а
ложно, и
ложно, если а
истинно.
Высказывание
![]() читается так: «Не а».
Таблица истинности для
читается так: «Не а».
Таблица истинности для
![]() имеет вид:
имеет вид:
-
а

0
1
1
0
Конъюнкцией высказываний a, b называется высказывание a ˄ b (a&b), которое истинно, если a и b истинны, и ложно, если хотя бы одно из них ложно. Высказывание a ˄ b читается: «a и b».
Дизъюнкцией высказываний a, b называется высказывание a ˅ b, которое истинно, если хотя бы одно из высказываний a или b истинно, и ложно, если оба они ложны. Читается: «a или b».
Импликацией
высказываний a,
b
называется высказывание
![]() ,
которое ложно, если a
истинно и b
ложно, и истинно во всех остальных
случаях. Читается: «Если a
, то b».
,
которое ложно, если a
истинно и b
ложно, и истинно во всех остальных
случаях. Читается: «Если a
, то b».
Эквивалентностью
(или эквиваленцией) высказываний a,
b
называется высказывание
![]() ,
которое истинно, если оба высказывания
a
и b
одновременно истинны или ложны, и ложно
во всех остальных случаях. Читается: «a
тогда и только тогда, когда b».
,
которое истинно, если оба высказывания
a
и b
одновременно истинны или ложны, и ложно
во всех остальных случаях. Читается: «a
тогда и только тогда, когда b».
Таблица истинности для этих логических операций такова:
|
a |
b |
a ˄ b |
a ˅ b |
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
1 |
1 |
Все высказывания можно разделить на простые (или элементарные) и составные (или сложные).
Всякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения выше определенных пяти логических операций, называется формулой алгебры логики.
Формулы алгебры логики будем обозначать большими латинскими буквами. Логические значения формулы при различных комбинациях значений входящих в нее высказываний можно описать посредством таблицы, которая называется таблицей истинности формулы.
Формула А, всегда истинная, называется тождественно истинной формулой или тавтологией и записывается А≡1. Формула В, всегда ложная, называется тождественно ложной формулой и записывается В≡0.
Пример 1. Среди следующий предложений выделить высказывания, установить, истинны они или ложны:
-
река Волхов впадает в озеро Ильмень;
-
всякий человек имеет брата;
-
пейте томатный сок!;
-
существует человек, который моложе своего отца;
-
который час?;
-
ни один человек не весит более 1000 кг;
-
23 < 5;
-
для всех действительных чисел х и у верно равенство х + у = у + х
-
х2-7х+12;
-
х2-7х+12=0.
Решение. Легко видеть, что высказывания 4), 6), 8) – истинные, а высказывания 1), 2), 7) – ложные. Предложения 3), 5), 9), 10 не являются высказываниями.
Пример 2. Пусть а – высказывание «Студент Иванов изучает английский язык», b – высказывание «Студент Иванов успевает по математической логике». Дать словесную формулировку высказываний:
-
a ˄
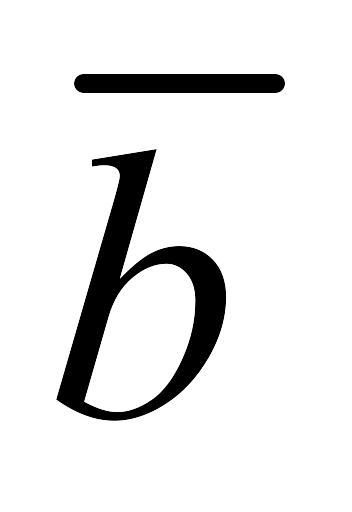 ; 2)
; 2)
 ; 3)
; 3)
 .
.
Решение. а) «Студент Иванов изучает английский язык и не успевает по математической логике»; б) «Если студент Иванов изучает английский язык, то он успевает по математической логике»; в) «Студент Иванов не успевает по математической логике тогда и только тогда, когда он не изучает английский язык».
Пример
3. Составить
таблицу истинности для высказывания a
˅
![]() .
.
Решение.
Таблица истинности для высказывания a
˅
![]() имеет
вид:
имеет
вид:
|
а |
b |
|
a
˅
|
|
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
Задания для контрольной работы № 1.
-
Какие из следующих предложений являются высказываниями:
-
Москва – столица России;
-
студент физико-математического факультета;
-
 ;
; -
Луна есть спутник Марса;
-
a ˃ 0.
-
Приведите примеры предложений,
-
являющихся высказываниями;
-
не являющихся высказываниями.
-
Верны ли утверждения:
-
сумма корней приведенного квадратного уравнения равна свободному члену;
-
сумма корней любого приведенного квадратного уравнения равна свободному члену;
-
существует приведенное квадратное уравнение, сумма корней которого равна свободному члену?
-
Установите, истинно или ложно высказывание:
-
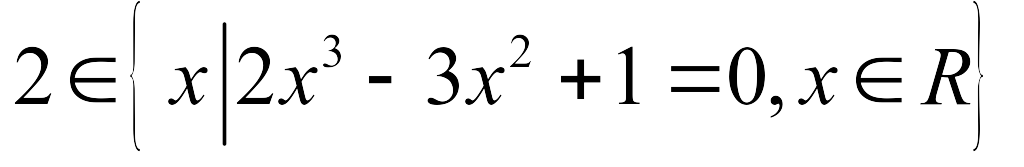 ;
; -
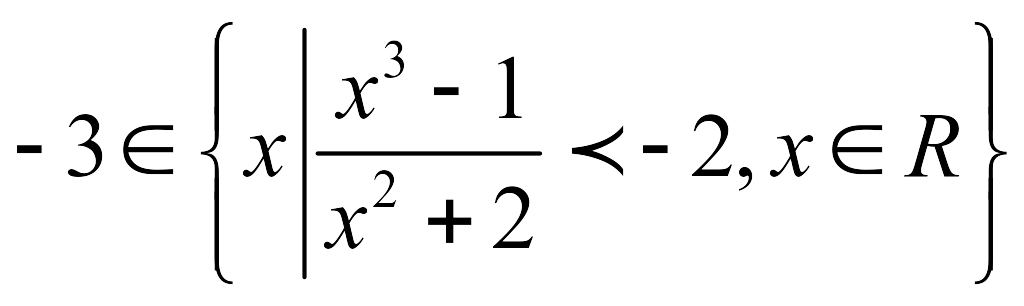 ;
; -
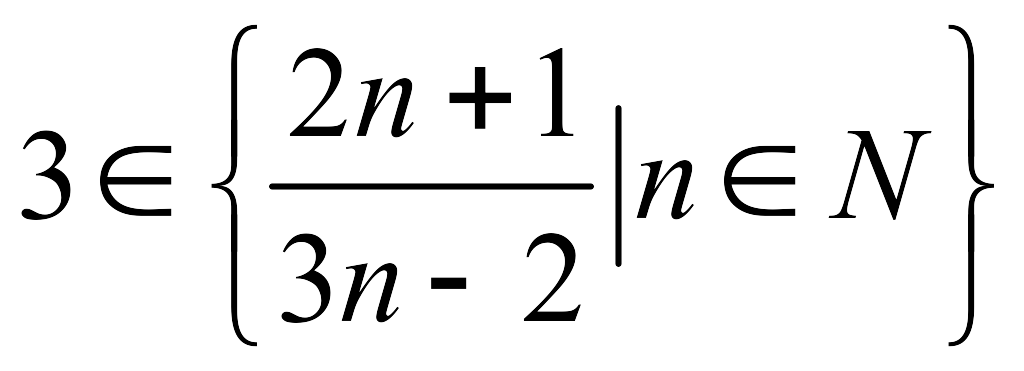 ;
; -

-
 ,
где
,
где
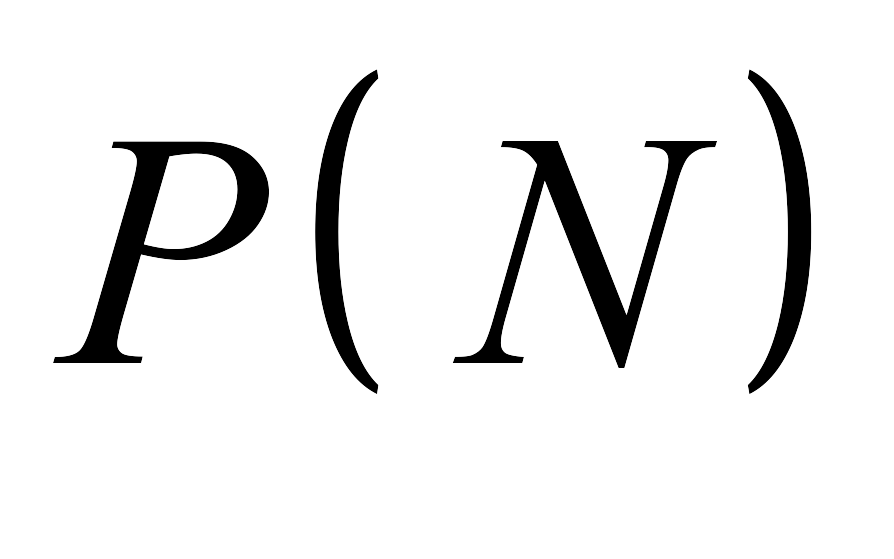 - множество всех подмножеств множества
N;
- множество всех подмножеств множества
N; -
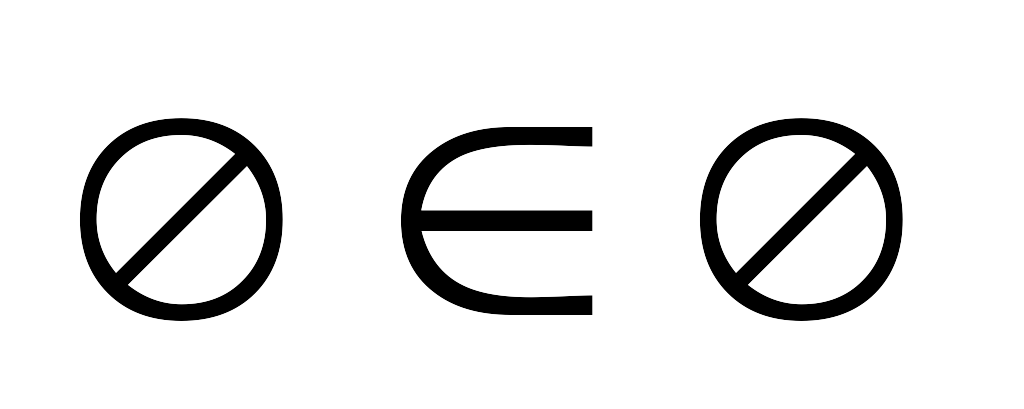 ;
; -
 ;
; -
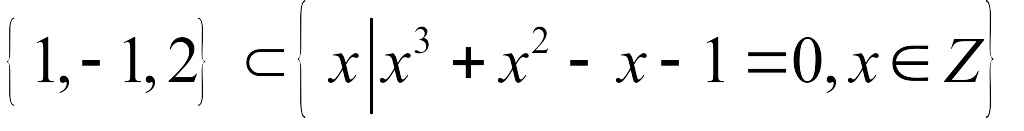 ;
; -
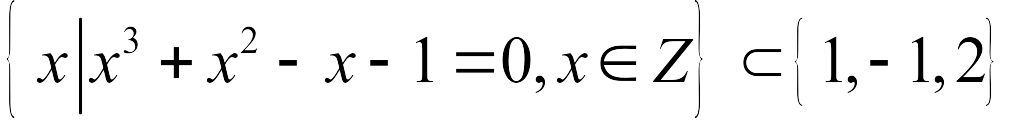 ;
; -
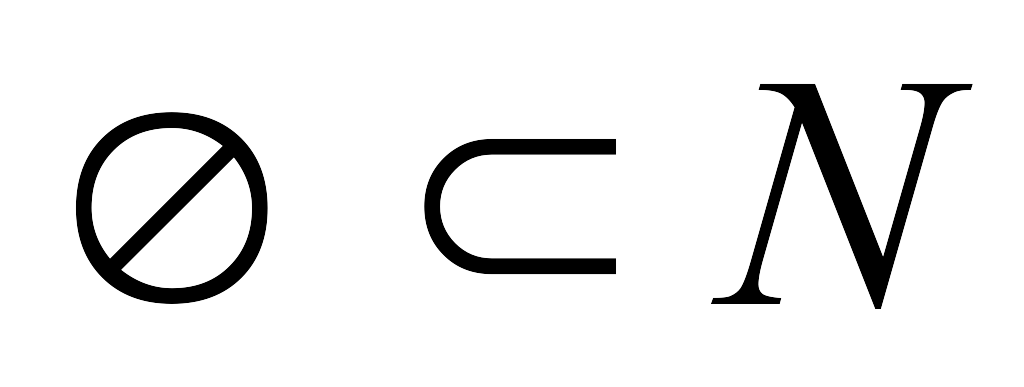 ;
; -
 ;
; -
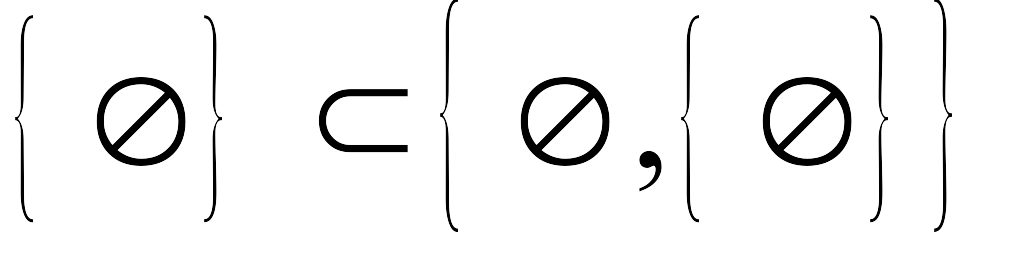 .
.
1.5.Является ли высказыванием следующее предложение: «Это предложение ложно»?
1.6.Среди следующих высказываний указать элементарные и составные. В составных высказываниях выделить грамматические связки:
1) число 27 не делится на 3;
2) число 15 делится на 5 и на 3;
3) если число 126 делится на 9, то оно делится на 3;
4) число 7 является делителем числа 42;
5) число 1269 делится на 9 тогда и только тогда, когда 18 делится на 9.
1.7.Обозначьте элементарные высказывания буквами и запишите следующие высказывания с помощью символов алгебры логики:
1) 45 кратно 3 и 42 кратно 3;
2) 45 кратно 3 и 12 не кратно 3;
3)
![]() или
или
![]() ;
;
4) 2 ≤ 5;
5) если число 212 делится на 3 и 4, то оно делится на 12;
6) число 212 – трехзначное число и кратно 3 или 4.
1.8.Пусть p и q обозначают высказывания:
p – «Я учусь в школе»;
q – «Я люблю математику».
-
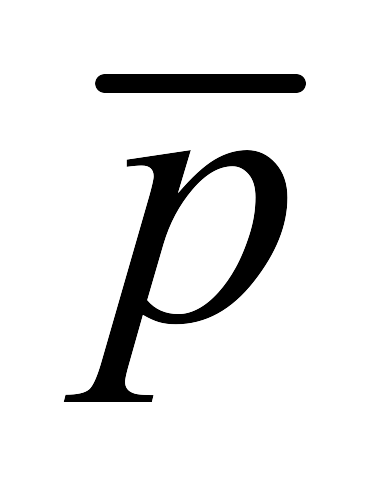 ; 5)
; 5)
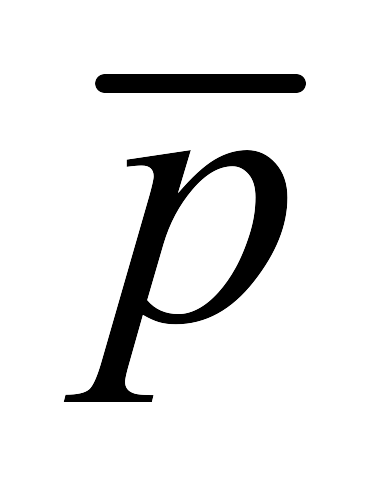 &q;
&q; -
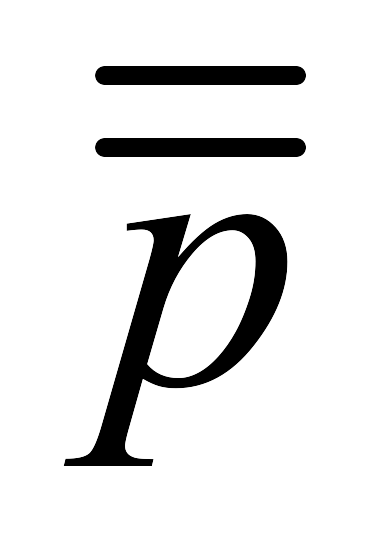 ; 6)
; 6)
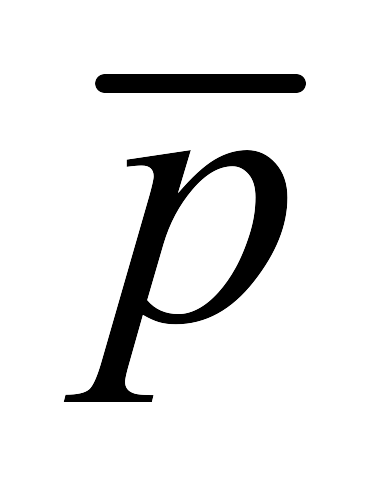 &
& ;
; -
p&q; 7)
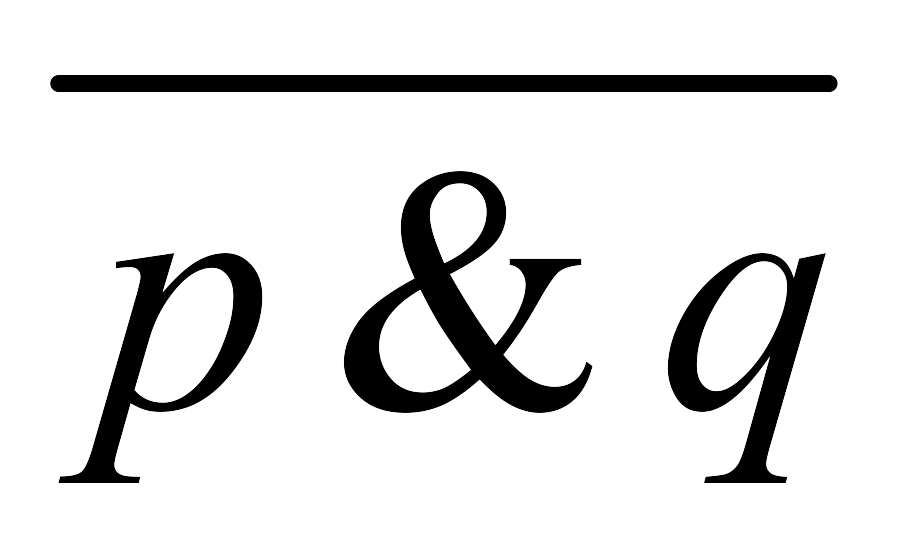 ;
; -
p&
 ; 8)
; 8)
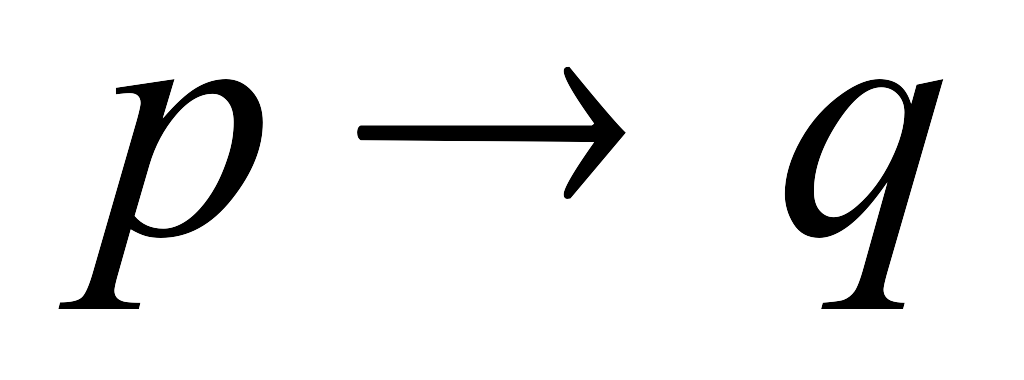 .
.
1.9.Какие из следующих импликаций истинны:
1)
если 2![]() 2=4,
то 2 < 3;
2=4,
то 2 < 3;
2)
если 2![]() 2=4,
то 2 ˃ 3;
2=4,
то 2 ˃ 3;
3)
если 2![]() 2=5,
то 2 < 3;
2=5,
то 2 < 3;
4)
если 2![]() 2=5,
то 2 ˃ 3?
2=5,
то 2 ˃ 3?
1.10.Выясните, в каких случаях приведенные ниже данные противоречивы:
1) а = 1, а&b = 0;
2) а = 1, а ˅ b = 0;
3) а = 1, а&b = 1;
4) а = 1, а ˅ b = 1;
5) а = 0, а&b = 1;
6) а = 0, а ˅ b = 1;
7) а = 0, а&b = 0;
8) а = 0, а ˅ b = 0.
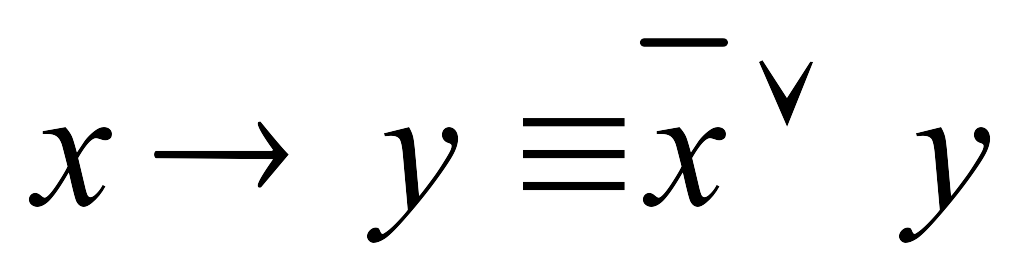
1.11.Пусть х, х’,у, у’ означают соответственно «7 – простое число», «7 – составное число», «8 – простое число», «8 – составное число»:
1) какие из предложений х&у, х&у’, х’&у, х’&у’ истинны и какие ложны?
2) то же с заменой конъюнкции на дизъюнкцию;
3)
то же для предложений
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
1.12.Проверить, не составляя таблиц истинности, являются ли следующие формулы тождественно истинными:
1)
![]() ; 8)
; 8)
![]() ;
;
2)
![]() ; 9)
; 9)
![]() ;
;
3)
![]() ; 10)
; 10)
![]() ;
;
4)
![]() ; 11)
; 11)
![]() ;
;
5)
![]() ; 12)
; 12)
![]() ;
;
6)
![]() ; 13)
; 13)
![]() ;
;
7)
![]() ; 14)
; 14)
![]() .
.
1.13. Найдите логические значения х и у , при которых выполняются равенства:
1)
![]() ;
;
2)
![]() .
.
1.14.
1)
Известно, что импликация
![]() истинна, а эквивалентность
истинна, а эквивалентность
![]() ложна. Что можно сказать о значении
импликации
ложна. Что можно сказать о значении
импликации
![]() ?
?
2)
Известно, что эквивалентность
![]() истинна. Что можно сказать о значении
истинна. Что можно сказать о значении
![]() и
и
![]() ?
?
3)
Известно, что х
имеет значение 1. Что можно сказать о
значениях импликации
![]() ;
;
![]() ?
?
4)
Известно, что
![]() имеет значение 1. Что можно сказать о
значениях
имеет значение 1. Что можно сказать о
значениях
![]() ;
;
![]() ;
;
![]() ?
?
1.15. Пусть х = 0, у = 1, z = 1. Определить логические значения нижеследующих сложных высказываний:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() .
.
1.16.
Показать,
что логические связки
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
где л
– фиксированное ложное высказывание,
имеют ту же таблицу истинности, что и
импликация
,
где л
– фиксированное ложное высказывание,
имеют ту же таблицу истинности, что и
импликация
![]() .
.
1.17.
1) Постройте с помощью отрицания и дизъюнкции формулу, таблица истинности для которой совпадала бы с таблицей для импликации.
2) Аналогично этому постройте с помощью отрицания и импликации формулу, таблица для которой совпадает с таблицей для дизъюнкции, и вторую формулу с таблицей, совпадающей с таблицей для конъюнкции.
1.18. Составить таблицы истинности для формул:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() .
.
1.19. Установите, какие из следующих формул являются тождественно истинными, тождественно ложными:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() .
.
Контрольная работа № 2. Равносильные формулы алгебры логики.
Определение. Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения на любом наборе значений входящих в них высказываний (А ≡ В).
Важнейшие равносильности можно разбить на три группы:
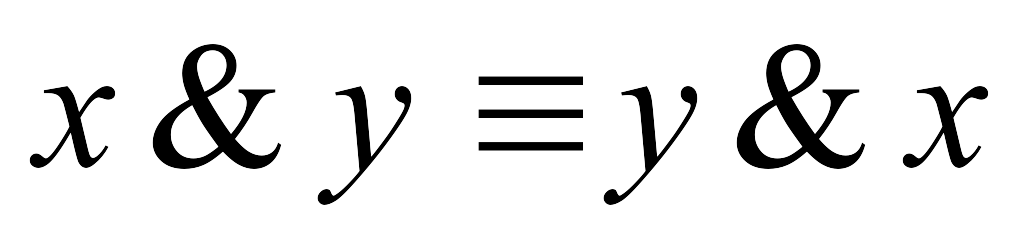
-
Основные равносильности.
![]() –законы
идемпотентности.
–законы
идемпотентности.
3.![]() .
.
4. х ˅ 1 ≡ 1.
5. х & 0 ≡ 0.
6. х ˅ 0 ≡ х.
7.
х
&![]() ≡ 0 – закон противоречия.
≡ 0 – закон противоречия.
8.
х
˅![]() ≡ 1 – закон исключенного третьего.
≡ 1 – закон исключенного третьего.
9.
![]() – закон снятия двойного отрицания.
– закон снятия двойного отрицания.
![]() –
законы
поглощения.
–
законы
поглощения.
-
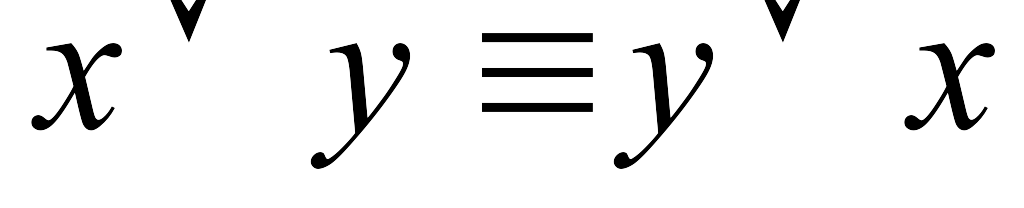
Равносильности, выражающие одни логические операции через другие.
-
 .
. -
 .
.
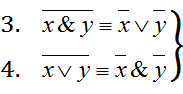 -
законы де Моргана.
-
законы де Моргана.
5.
![]() .
.
6.
![]() .
.
-
Равносильности, выражающие основные законы алгебры логики.
-
 .
. -
 .
. -
 .
. -
 .
. -
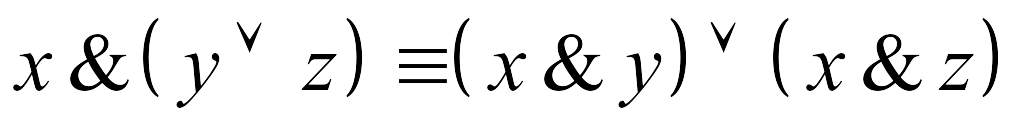 .
. -
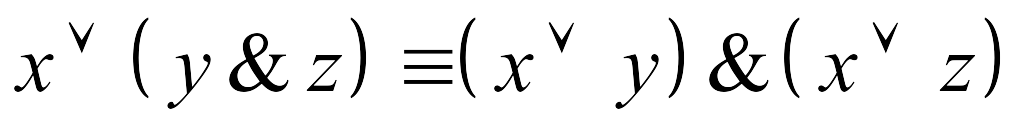 .
.
Используя равносильности групп I, II, III, можно часть формулы алгебры логики или всю формулу заменить равносильной ей формулой. Такие преобразования называются равносильными. Равносильные преобразования формул применяются для доказательства равносильностей, для приведения формул к заданному виду, для упрощения формул.
Пример
1. Доказать
равносильность
![]() .
.
Решение. Для доказательства равносильности подвергнем ее левую часть равносильным преобразованиям:
![]() .
.
Пример
2. Упростить
формулу
![]() .
.
Решение. Подвергнем формулу А равносильным преобразованиям:
![]()
![]()
![]() .
.
Пример
3. Доказать
что формула
![]() тождественно истинная.
тождественно истинная.
Решение. Подвергнем формулу А равносильным преобразованиям:
![]()
![]() .
.
Задания для контрольной работы № 2.
1.20. Доказать равносильность:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() .
.
1.21. Упростить формулу:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() .
.
1.22. Доказать тождественную истинность или тождественную ложность формул:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() ;
;
15)
 .
.
1.23.
Пусть F
- тождественно ложная формула. Доказать,
что
![]() .
.
1.24.
Найдите х,
если
![]() .
.
1.25. Последовательность высказываний (аn) определяется следующим рекуррентным соотношением:
![]() ,
n
˃ 3.
,
n
˃ 3.
Высказывания а1, а2, а3 заданы, причем а1 и а3 истинны, а а2 ложно. Истинно или ложно высказывание аn? Как выражается аn через а1, а2, а3?
1.26. Выразить все основные операции:
1) через дизъюнкцию, конъюнкцию и отрицание;
2) через конъюнкцию и отрицание;
3) через дизъюнкцию и отрицание;
4) через импликацию и отрицание.
1.27. 1) Выразить отрицание импликации через основные операции так, чтобы отрицания стояли только над аргументами.
2) Выразить операцию дизъюнкции через импликацию.
1
 .28.
Исключающей
дизъюнкцией двух высказываний а
и b
называется новое высказывание,
обозначаемое а
˅ b
(читают «либо а,
либо b»),
которое истинно, когда одно и только
одно из данных высказываний истинно, и
ложно в остальных случаях. Составить
таблицу истинности исключающей дизъюнкции
и выразить ее через основные операции
над высказываниями.
.28.
Исключающей
дизъюнкцией двух высказываний а
и b
называется новое высказывание,
обозначаемое а
˅ b
(читают «либо а,
либо b»),
которое истинно, когда одно и только
одно из данных высказываний истинно, и
ложно в остальных случаях. Составить
таблицу истинности исключающей дизъюнкции
и выразить ее через основные операции
над высказываниями.
1.29.
Штрихом
Шеффера двух высказываний а
и b
называется новое высказывание,
обозначаемое
![]() (читают «а
не совместно с b»),
которое ложно только тогда, когда оба
данные высказывания истинны. Составить
таблицу истинности штриха Шеффера и
выразить его через основные операции
над высказываниями. Доказать, что все
основные операции над высказываниями
можно выразить через штрих Шеффера.
(читают «а
не совместно с b»),
которое ложно только тогда, когда оба
данные высказывания истинны. Составить
таблицу истинности штриха Шеффера и
выразить его через основные операции
над высказываниями. Доказать, что все
основные операции над высказываниями
можно выразить через штрих Шеффера.
1.30.
Штрихом Лукасевича двух высказываний
а
и b
называется новое высказывание ![]() (читают «ни а,
ни b»),
которое истинно в том и только том
случае, когда оба данные высказывания
ложны. Составить таблицу истинности
штриха Лукасевича и выразить его через
основные операции над высказываниями.
Доказать, что все основные операции над
высказываниями можно выразить через
штрих Лукасевича.
(читают «ни а,
ни b»),
которое истинно в том и только том
случае, когда оба данные высказывания
ложны. Составить таблицу истинности
штриха Лукасевича и выразить его через
основные операции над высказываниями.
Доказать, что все основные операции над
высказываниями можно выразить через
штрих Лукасевича.
1.31. Доказать, что операция отрицания не может быть выражена через основные операции (бинарные) над высказываниями.
1.32. Можно ли для каждой формулы найти равносильную, не содержащую отрицания?
1.33. Мальчик решил в воскресенье закончить чтение книги, сходить в музей или кино, а если будет хорошая погода – пойти на реку выкупаться. В каком случае можно сказать, что решение мальчика не выполнено? В ответе отрицания должны содержаться лишь в простых высказываниях.
Контрольная работа № 3. Совершенные нормальные формы.
Определение 1. Функцией алгебры логики n переменных называется любая функция n переменных F (х1, х2, …, хn), аргументы которой принимают два значения 1 и 0, и сама функция принимает одно из двух значений:1 или 0.