Файл: Методика АСУТП контрольная работа.doc

Всякая формула алгебры логики есть функция алгебры логики. Тождественно истинная и тождественно ложная формулы есть постоянные функции.

Можно показать, что всякую функцию алгебры логики можно представить в виде формулы алгебры логики, и это представление таково:

. (*)

Формулу (*) можно преобразовать к формуле, которая содержит только элементарные переменные высказывания и обладает следующими свойствами совершенства (или свойствами (С)):

1) каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F (х₁, х₂, …, х_n);

2) все логические слагаемые формулы различны;

3) ни одно логическое слагаемое формулы не содержит одновременно переменную и ее отрицание;

4) ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.

С помощью таблицы истинности, определяющей функцию F (х₁, х₂, …, х_n), легко получить соответствующую формулу алгебры логики, обладающую свойствами (С). Действительно, для каждого набора значений переменных, на котором функция F (х₁, х₂, …, х_n) принимает значение 1, запишем конъюнкцию элементарных переменных высказываний, взяв за член конъюнкции х_k, если значение х_k на указанном наборе значений переменных есть 1, и отрицание х_k, если значение х_k есть 0. Дизъюнкция всех полученных таким образом конъюнкций и будет искомой формулой.

Определение 2. Элементарной конъюнкцией n переменных называется конъюнкция переменных или их отрицаний.

Определение 3. Дизъюнктивной нормальной формой (ДНФ) формулы А называется равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций.

Определение 4. Совершенной дизъюнктивной нормальной формой (СДНФ) формулы А называется ДНФ А, обладающая свойствами (С).

СДНФ можно получить двумя способами: а) с помощью таблицы истинности (см. выше); б) с помощью равносильных преобразований.

Правило получения СДНФ из формулы А с помощью равносильных преобразований.

1. Для формулы А получаем любую ДНФ.

2. Из ДНФ А путем равносильных преобразований получаем СДНФ, последовательно добиваясь выполнения четырех свойств СДНФ:

1) Пусть В есть слагаемое ДНФ, не содержащее х_i. Тогда надо заменить слагаемое В в ДНФ А на слагаемое .

2) Если в ДНФ А встретится два одинаковых слагаемых , то лишнее нужно отбросить, так как .

3) Если слагаемое В в ДНФ А содержит конъюнкцию , то это слагаемое можно отбросить, так как ,и следовательно, , а ложное высказывание из дизъюнкции можно выбросить (в силу равносильности ).

4) Если в некоторое слагаемое В в ДНФ А переменная х_i входит дважды, то лишнюю переменную надо отбросить, так как .

Определение 5. Элементарной дизъюнкцией n переменных называется дизъюнкция переменных или их отрицаний.

Определение 6. Конъюнктивной нормальной формой (КНФ) формулы А называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.

Определение 7. Совершенной конъюнктивной нормальной формой формулы А (СКНФ А) называется КНФ А, удовлетворяющая четырем свойствам:

1. все элементарные дизъюнкции, входящие в КНФ А, содержат все переменные;

2. все элементарные дизъюнкции, входящие в КНФ А, различны;

3. ни одна элементарная дизъюнкция, входящая в КНФ А, не содержит переменную и ее отрицание;

4. каждая элементарная дизъюнкция, входящая в КНФ А, содержит переменную один раз.

СКНФ А можно получить двумя способами: а) с помощью таблицы истинности (используя закон двойственности , получаем с помощью таблицы истинности СДНФ , и, взяв отрицание СДНФ , получаем СКНФ А); б) с помощью равносильных преобразований.

Правило получения СКНФ из формулы А с помощью равносильных преобразований.

1. Для формулы А получаем любую КНФ.

2. Из КНФ А путем равносильных преобразований получаем СКНФ А, последовательно добиваясь выполнения четырех свойств СКНФ.

1. Если элементарная дизъюнкция В, входящая в КНФ А, не содержит переменную х_i , тогда заменяем В на .

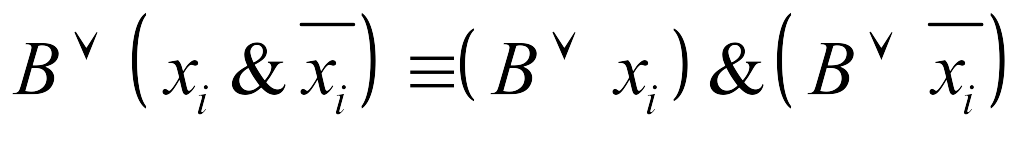2. Если КНФ А содержит две одинаковых элементарных дизъюнкции, то одну можно отбросить, так как .

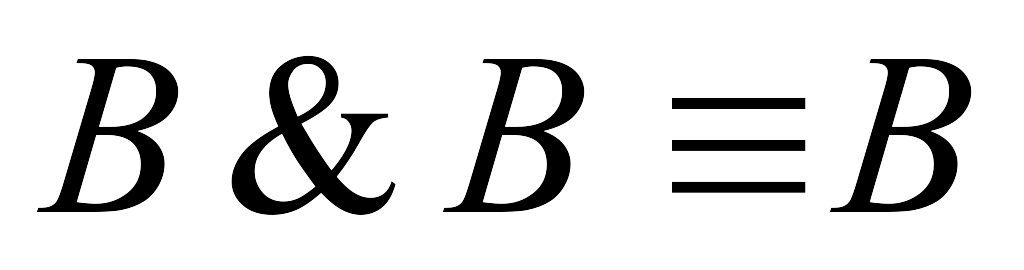3. Если в элементарную дизъюнкцию В входит пара 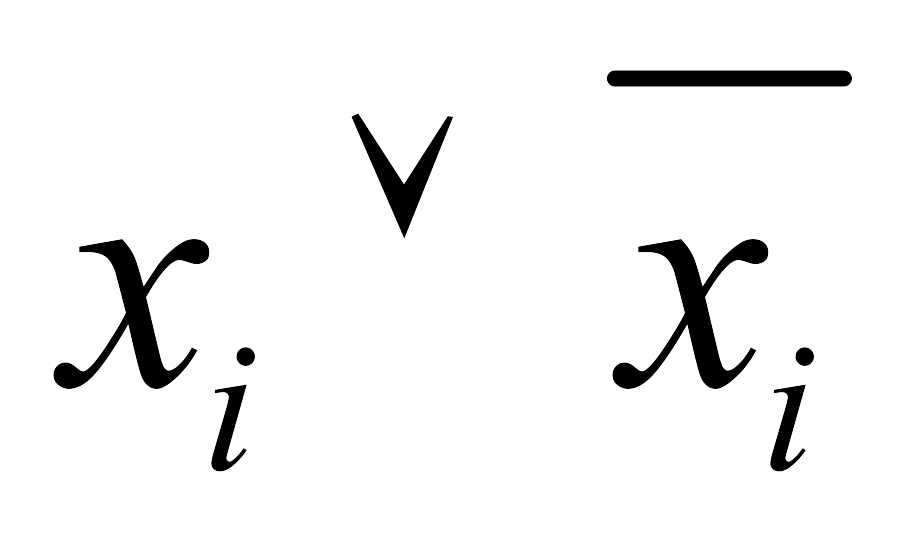, а значит и 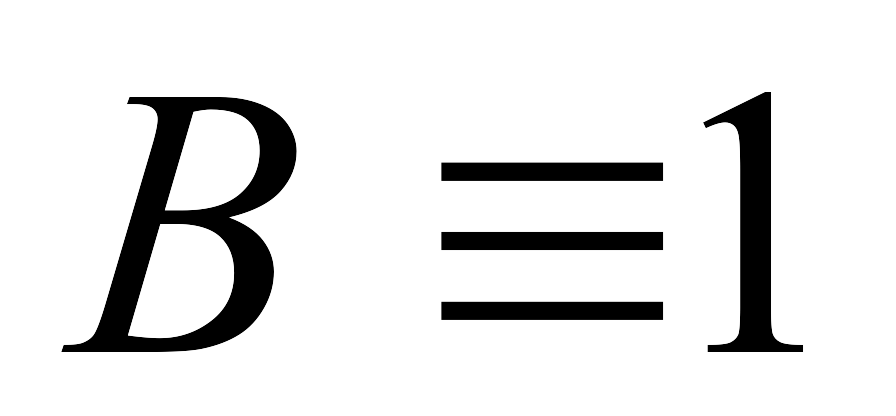, то ее можно отбросить, так как , и истинное высказывание из конъюнкции можно выбросить (в силу равносильности ).

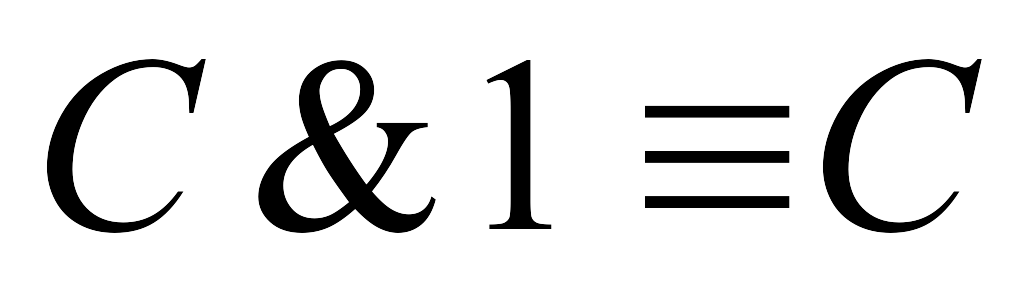4. Если в некоторую элементарную дизъюнкцию В переменная х_i входит дважды, то лишнюю переменную нужно отбросить, так как .

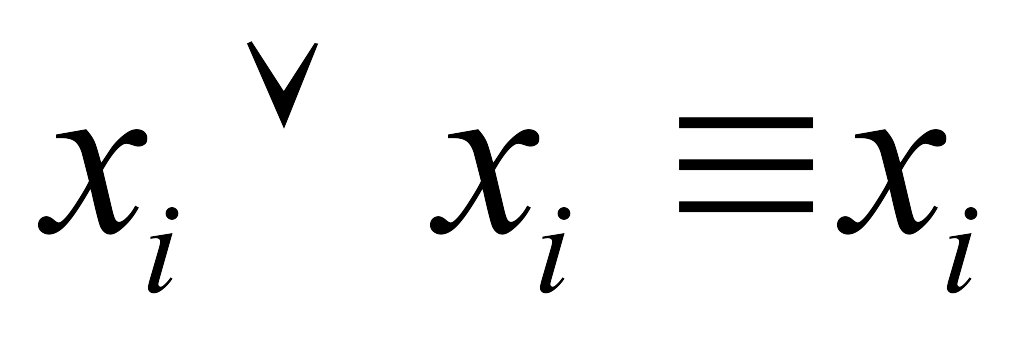Пример 1. Найти формулу, определяющую функцию ф (x, y, z), по заданной таблице истинности:

х	у	z	ф (x, y, z)
1	1	1	1
1	1	0	0
1	0	1	0
1	0	0	0
0	1	1	1
0	1	0	1
0	0	1	1
0	0	0	1

Решение. Используя правило получения формулы алгебры логики из таблицы истинности для функции ф (x, y, z), получим:

Упростив эту формулу, получим:

.

Таким образом, искомой формулой, определяющей функцию ф (x, y, z), можно считать , или , или какую-нибудь другую из равносильных им формул.

Пример 2. Следующую формулу привести к СДНФ, предварительно приведя ее равносильными преобразованиями к ДНФ: .

Решение.

Ответ. .

Пример 3. Для формулы из примера 2 найти СДНФ путем составления таблицы истинности.

Решение. Составим таблицу истинности для формулы .

Тогда СДНФ .

Пример 4. Для формулы из примера 2 найти СКНФ путем равносильных преобразований, предварительно приведя ее к КНФ.

Решение. Из примера 2: . Далее .

СКНФ А.

Ответ. СКНФ А .

Пример 5. Для формулы из примера 2 найти СКНФ, записать предварительно СДНФ ее отрицания, а потом воспользовавшись формулой двойственности.

Решение. СДНФ .

.

Все формулы алгебры логики делятся на три класса:

1. тождественно истинные;

2. тождественно ложные;

3. выполнимые.

Формулу А называют выполнимой, если она принимает значение 1 хотя бы на одном наборе значений входящих в нее переменных и не является тождественно истинной.

Теорема. Для того, чтобы формула алгебры логики была тождественно истинна (ложна), необходимо и достаточно, чтобы любая элементарная дизъюнкция (конъюнкция), входящая в КНФ А (ДНФ А), содержала переменную и ее отрицание.

Пример 6. Будет ли формула тождественно истинной, тождественно ложной или выполнимой?

Решение. Приведем формулу к какой-либо нормальной форме:

.

Полученная ДНФ не является тождественно ложной, так как каждая элементарная конъюнкция не содержит переменную и ее отрицание. Следовательно, исходная формула тождественно истинна или выполнима. Преобразуем данную формулу в КНФ:

.

Это произведение не является тождественно истинным, так как элементарная сумма не тождественно истинна. Таким образом, исходная формула не тождественно ложна и не тождественно истинна, следовательно, она выполнима.

Задания для контрольной работы № 3.

1.34. По таблицам истинности найдите формулы, определяющие функции F₁ (x, y, z), F₂ (x, y, z), F₃ (x, y, z), F₄ (x, y, z), и придайте им более простой вид:

1.35. Пусть F (l₁, l₂, l₃) – булевая функция, которая принимает значение 1 тогда и только тогда, когда точно одна из переменных принимает значение 1. Составьте таблицу истинности для функции F (l₁, l₂, l₃) и выразите эту функцию через основные логические операции.

1.36. Назовем функцией большинства булеву функцию от трех переменных, значение которой совпадает с тем значением, которое принимает большинство переменных.

а) Составьте таблицу, определяющую функцию большинства и выразите эту функцию через основные операции.

б) Упростите выражение .

1.37. Булева функция F* (l₁, l₂,…, l_n) называется двойственной по отношению к булевой функции F (l₁, l₂,…, l_n), если:

.

Для каждой булевой функции от двух переменных найдите двойственную ей булеву функцию.

1.38. Булева функция F (l₁, l₂,…, l_n) называется:

а) сохраняющей 0, если F (0, 0,…, 0) = 0;

б) сохраняющей 1, если F (1, 1,…, 1) = 1.

Среди булевых функций от одной и двух переменных найти все функции, сохраняющие 1, и все функции, сохраняющие 0.

1.39. Для следующих формул найти СДНФ и СКНФ, каждую двумя способами (путем равносильных преобразований и используя таблицы истинности):

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) ;

10) .

1.40. Найдите СДНФ для всякой тождественно истинной формулы, содержащей: 1) одно переменное; 2) два переменных; 3) три переменных.

1.41. Найдите СКНФ для всякой тождественно ложной формулы, содержащей: 1) одно переменное; 2) два переменных; 3) три переменных.

1.42. Докажите равносильность формул и сравнением их совершенных нормальных форм (конъюнктивных и дизъюнктивных).

1.43. Найдите более простой вид формул, имеющих следующие совершенные нормальные формы:

1) ;

2) ;

3) ;

4) .

1.44. Используя критерий тождественной истинности и тождественной ложности формул, установить, будет ли данная формула тождественно истинной, тождественно ложной или выполнимой:

1) ;

2) ;

3) ;

4) ;

5) ;

6) .

Контрольная работа № 4. Приложение алгебры высказываний к релейно-контактным схемам (РКС).

Релейно-контактные схемы (их часто называют переключательными схемами) широко используются в технике автоматического управления.

Под переключательной схемой понимают схематическое изображение некоторого устройства, состоящее из следующих элементов:

1. переключателей, которыми могут быть механические устройства, электромагнитные реле, полупроводники и т.д.;

2. соединяющие их проводники;

3. входы в схему и выходы из нее (клеммы, на которые подается электрическое напряжение). Они называются полюсами.

Простейшая схема содержит один переключатель Р и имеет один вход А и один выход В. Переключателю Р поставим в соответствие высказывание р, гласящее: «Переключатель Р замкнут». Если р истинно, то импульс, поступающий на полюс А, может быть снят на полюсе В без потери напряжения, т.е. схема пропускает ток. Если р ложно, то переключатель разомкнут, и схема тока не проводит. Таким образом, если принять во внимание не смысл высказывания, а только его значение, то можно считать, что любому высказыванию может быть поставлена в соответствие переключательная схема с двумя полюсами (двухполюсная схема).

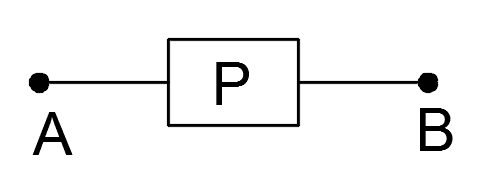
Формулам, включающим основные логические операции, также могут быть поставлены в соответствие переключательные схемы.

Так, конъюнкции двух высказываний p&q ставится в соответствие схема:

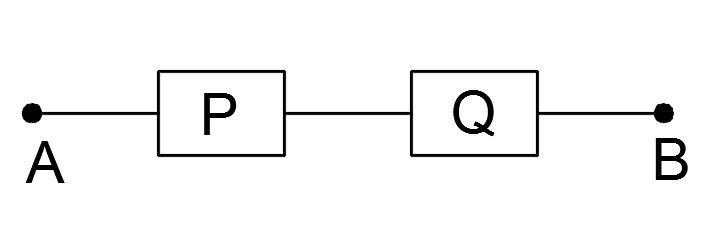
а дизъюнкции схема:

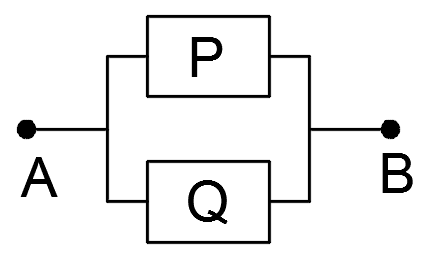
Так любая формула алгебры логики может быть записана в ДНФ или КНФ, то ясно, что каждой формуле алгебры логики можно поставить в соответствие некоторую РКС, а каждой РКС можно поставить в соответствие некоторую формулу алгебры логики. Поэтому возможности схемы можно выявить, изучая соответствующую ей формулу, а упрощение схемы можно свести к упрощению формулы.

Пример 1. Составить РКС для формулы .

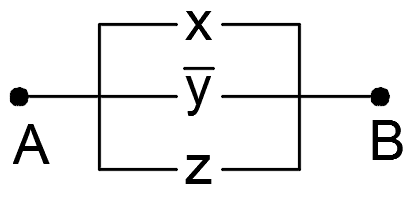
Решение. Упростим данную формулу с помощью равносильных преобразований:

.

Тогда РКС для данной формулы имеет вид:

Пример 2. Упростить РКС:

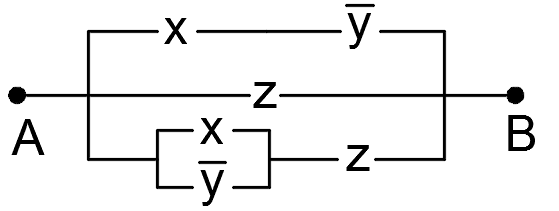
Решение. Составим по данной РКС формулу (функцию проводимости) и упростим её:

(к последним двум слагаемым применили закон поглощения).

Тогда упрощенная схема выглядит так:

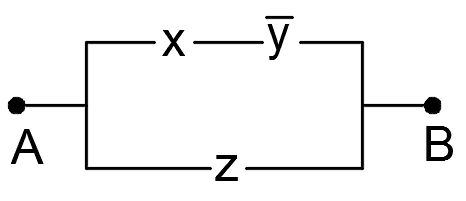
Условие логической задачи с помощью соответствующих обозначений записывают в виде формулы алгебры логики. После равносильных преобразований формулы получают ответ на все вопросы задачи.

Пример 3. После обсуждения состава участников предполагаемой экспедиции было решено, что должны выполняться два условия:

а) если поедет Арбузов, то должны поехать еще Брюквин или Вишневский;

б) если поедут Арбузов и Вишневский, то поедет и Брюквин.

Требуется:

1) ввести краткие обозначения для сформулированных условий и составить логическую формулу, выражающую принятое решение в символической форме;

2) для полученной формулы найти возможно более простую равносильную формулу;

3) пользуясь найденной более простой формулой, дать новую или более простую словесную формулировку принятого решения о составе участников экспедиции.

Решение. 1. Назначение в экспедицию Арбузова, Брюквина и Вишневского обозначим буквами А, Б, В соответственно. Тогда условие а) можно записать в виде , а условие б) в виде . Так как оба условия должны выполняться одновременно, то они должны быть соединены логической связкой «и». Поэтому принятое решение можно записать в виде следующей символической формулы: .

2.

.

3. Символическую формулу читаем так: «Если поедет Арбузов, то поедет и Брюквин». Это и есть наиболее простая словесная формулировка принятого решения о составе экспедиции.

Задания для контрольной работы № 4.

1.45. Составить РКС для формулы:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) .

1.46. Построить схемы, реализующие следующие булевы операции:

1) импликацию ;

2) эквивалентность ;

3) альтернативу (см. задачу 1.28);

4) штрих Шеффера (см. задачу 1.29);

5) штрих Лукасевича (см.задачу 1.30).

1.47. Построить РКС для F (x, y, z), если известно, что:

1) F (0, 1, 0) = F (1, 0, 1) = F (1, 1, 1) = 1;

2) F (1, 0, 1) = F (1, 1, 0) = 1;

3) F (0, 0, 1) = F (0, 1, 1) = F (1, 0, 1) = F (1, 1, 1) = 1;

4) F (1, 1, 0) = F (1, 1, 1) = 1;

5) F (0, 0, 1) = F (1, 0, 1) = F (1, 0, 0) = 1;

6) F (0, 0, 1) = F (0, 1, 0) = F (0, 1, 1) = F (1, 0, 1) = 1,

а остальные значения функции F равны нулю.

1.48. Упростить РКС:

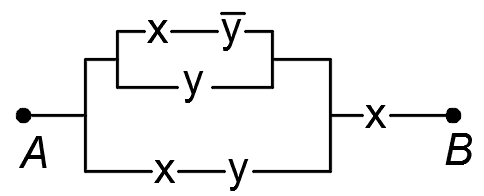
1)

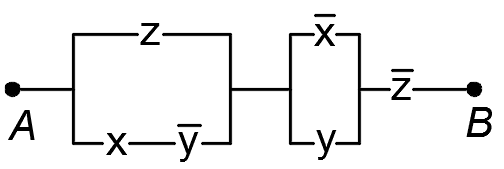
2)

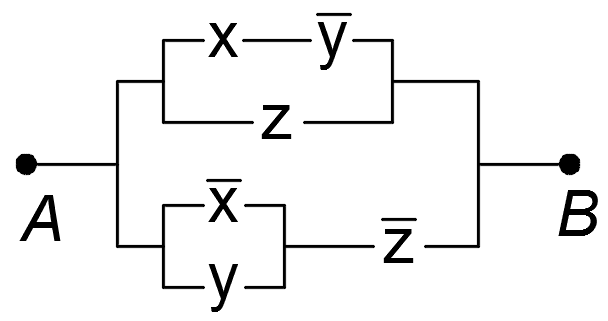
3)

4 )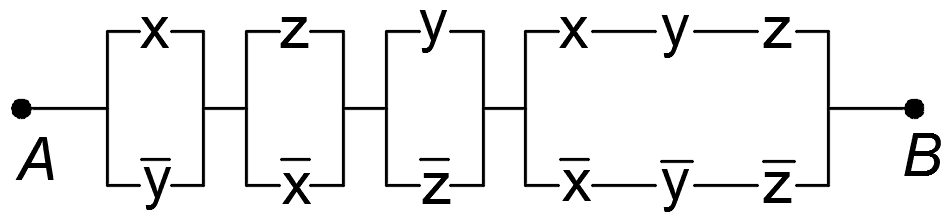

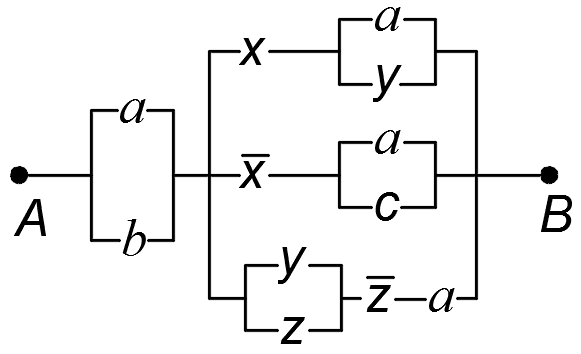
5)

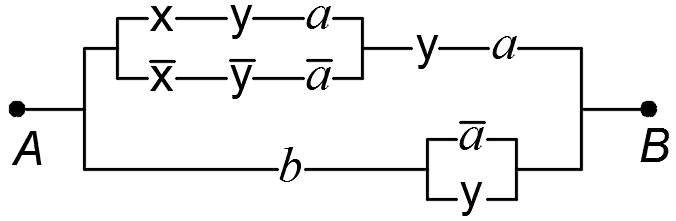
6)

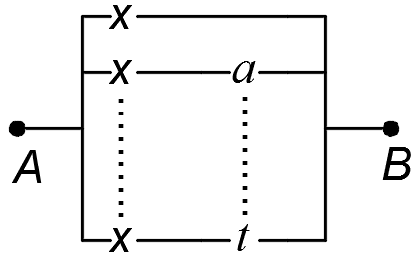
7)

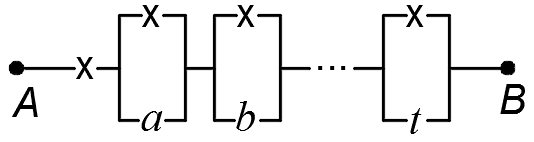
8)

1.49. По данной схеме найти функцию проводимости и условия работы:

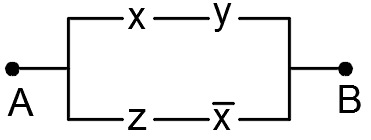
1)

2 )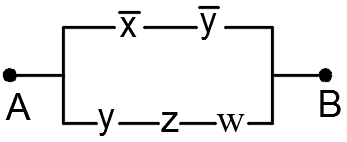

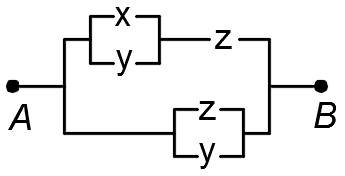
3)

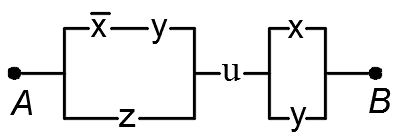
4)

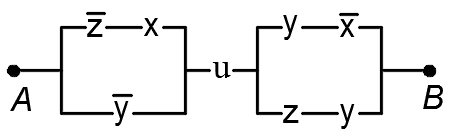
5)

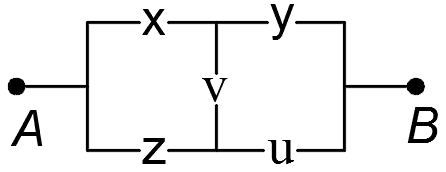
6)

1.50. Проверить равносильность схем:

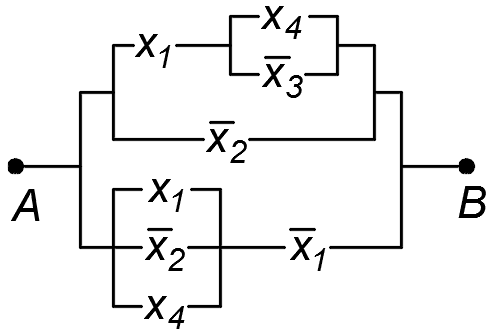
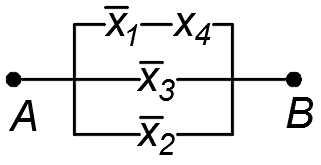
1)

2 )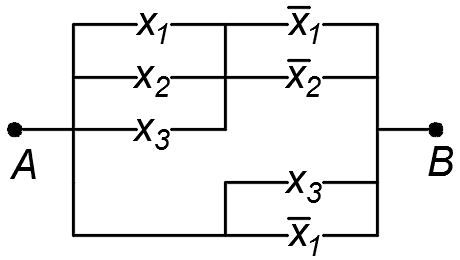

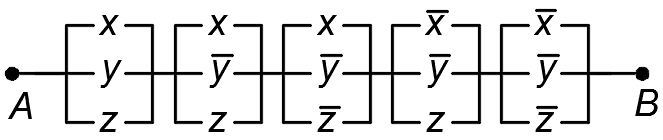
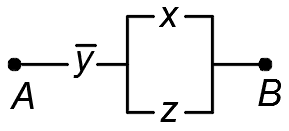
3)

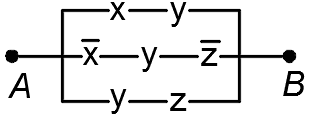
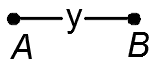
4)

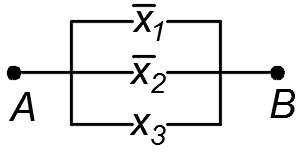
1.51. Электрическая цепь, изображенная на рис. 1, содержит только двухпозиционные выключатели (при одном состоянии переключателя ток через него проходит, при другом не проходит). Можно ли эту цепь заменить более простой цепью, изображенной на рис. 2?

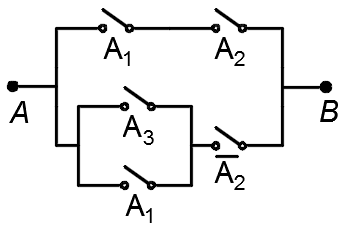
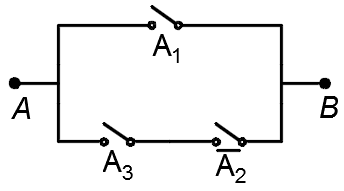
Рис. 1 Рис. 2