Файл: Курсовая Принятие решений на примере задачи распознавания образов с использованием алгоритма Дискриминантная функция.doc
ВУЗ: Государственный университет природы, общества и человека «Дубна»
Категория: Курсовая работа
Дисциплина: Методы оптимальных решений
Добавлен: 23.10.2018
Просмотров: 2071
Скачиваний: 46
Международный университет природы, общества и человека «Дубна»
Кафедра системного анализа и управления
Курсовая работа
Принятие решений на примере задачи распознавания образов с использованием алгоритма «Дискриминантная функция»
по курсу «Теория принятия решений»
Выполнила: студентка II курса гр. 2014
Хлупина А.А.
Ст. преподаватель: Булякова И.А.
Дубна, 2007
Содержание
Введение
Дискриминантный анализ — это раздел математической статистики, содержанием которого является разработка методов решения задач различения (дискриминации) объектов наблюдения по определенным признакам.
Методы дискриминантного анализа находят применение в различных областях: медицине, социологии, психологии, экономике и т.д. При наблюдении больших статистических совокупностей часто появляется необходимость разделить неоднородную совокупность на однородные группы (классы). Такое расчленение в дальнейшем при проведении статистического анализа дает лучшие результаты моделирования зависимостей между отдельными признаками.
Дискриминантный анализ оказывается очень удобным и при обработке результатов тестирования отдельных лиц. Например, при выборе кандидатов на определенную должность можно всех опрашиваемых претендентов разделить на две группы: «подходит» и «не подходит».
Можно привести еще один пример применения дискриминантного анализа в экономике. Для оценки финансового состояния своих клиентов при выдаче им кредита банк классифицирует их на надежных и ненадежных по ряду признаков. Таким образом, в тех случаях, когда возникает необходимость отнесения того или иного объекта к одному из реально существующих или выделенных определенным способом классов, можно воспользоваться дискриминантным анализом.
Теоретическая часть
Дискриминантный анализ используется для решение задач распознавания в ситуациях, когда в материале обучения (МО) представлены объекты K образов (K=2,3,…), распределенные нормально.
Метод решения задачи.
Дискриминантный анализ основан на предположении, что объекты, составляющие каждый из образов, многомерно нормально распределены. Мы опираемся на эталонные объекты. Теоретически разделяются:
— линейный дискриминантный анализ, когда матрицы ковариации для разных образов равны;
— квадратичный дискриминантный анализ, когда матрицы ковариации для разных объектов различны.
Линейный дискриминантный анализ.
Рассмотрим случай, когда в МО имеется два образа. Оказывается, что при равных ковариационных матрицах поверхность с одной стороны, от которой больше вероятность принадлежности к одному из образов, а с другой к другому (критерий Байеса), является гиперплоскость, т.е. линейная поверхность размерности n-1 (n – размерность пространства). Уравнение гиперплоскости в общем виде можно записать следующим образом:
![]() .
.
В данном случае эта поверхность вычисляется следующим образом:
![]() (1),
(1),
где
![]() – n-мерный вектор столбец
в пространстве свойств
– n-мерный вектор столбец
в пространстве свойств
![]() ;
;
![]() – математическое
ожидание (среднее) объектов 1-го образа;
– математическое
ожидание (среднее) объектов 1-го образа;
![]() – математическое
ожидание (среднее) объектов 2-го образа;
– математическое
ожидание (среднее) объектов 2-го образа;
![]() – транспонирование;
– транспонирование;
![]() – матрица
коэффициентов ковариации.
– матрица
коэффициентов ковариации.
Формула (1) называется уравнением линейной дискриминантной функции.
Коэффициенты ковариации вычисляются следующим образом:
![]() ,
,
где M – знак математического ожидания.
Коэффициенты ковариации тесно связан с коэффициентом корреляции:
![]() ,
,
где
![]() — среднее квадратичное отклонение (
— среднее квадратичное отклонение (![]() )
i-го свойства;
)
i-го свойства;
![]() — среднее
квадратичное отклонение (
— среднее
квадратичное отклонение (![]() )
j-го свойства;
)
j-го свойства;
Дисперсия
![]() .
.
Дискриминантная
плоскость разбивает все пространство
на две части. При этом точки пространства,
относимые к 1-му образу, при подстановки
своих координат в дискриминантную
функцию дадут
![]() ,
а точки 2-го образа —
,
а точки 2-го образа —
![]() .
.
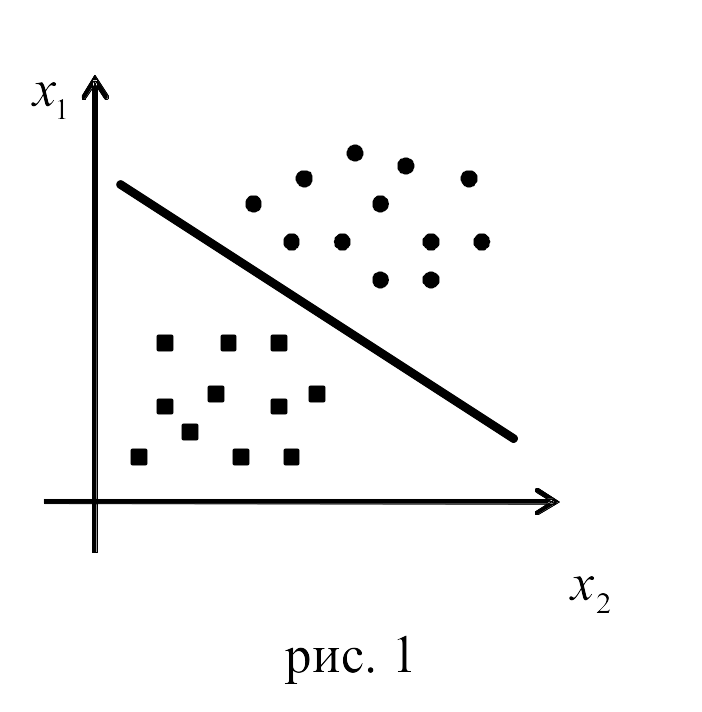
Таким образом, подставляя координаты, интересующих нас объектов выборки, мы по дискриминантной функции определим, к какому из двух образов принадлежит объект (понятно, что с определенной долей вероятности). На рисунке (рис. 1) для двумерного случая это выглядит следующим образом:
Значение матриц ковариации вычисляются по формулам:
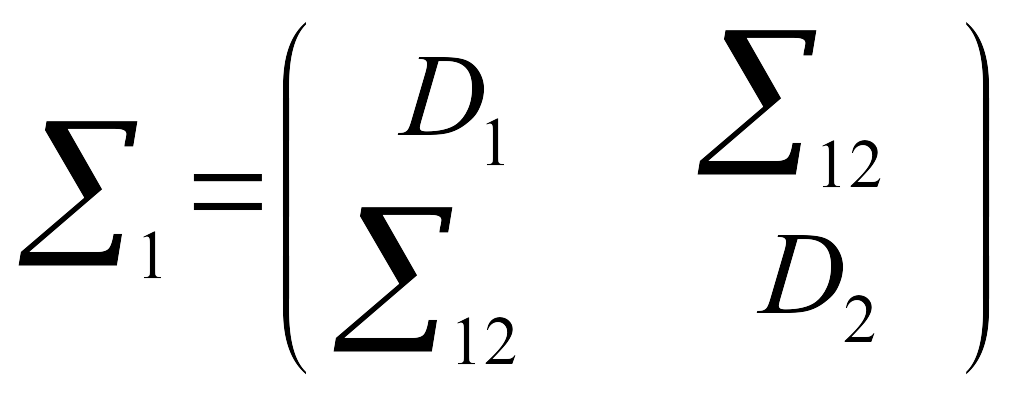 ;
;
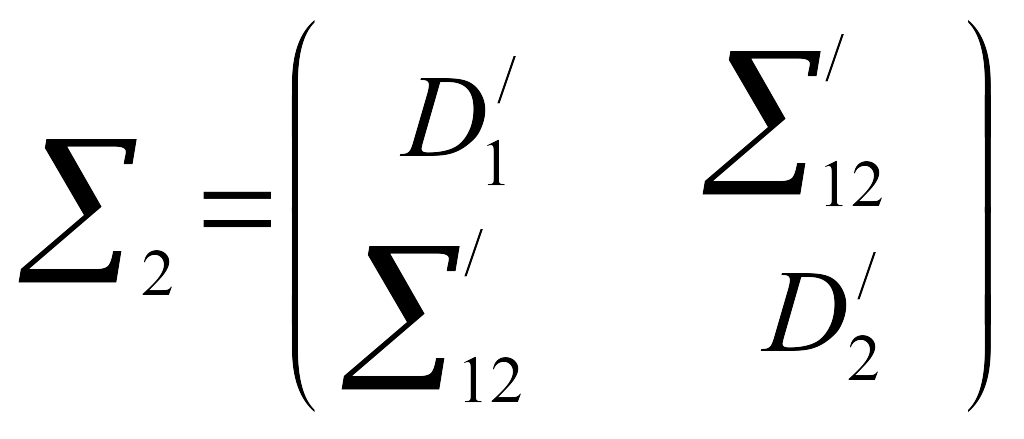 .
.
Есть параметр, говорящий о качестве разбиения с помощью дискриминантной функции – это расстояние Махаланобиса:
![]() .
.
Разбиение тем
лучше, чем больше
![]() .
.
Квадратичный дискриминантный анализ.
Был рассмотрен случай, когда матрицы ковариации для разных образов равны, и для распознавания использовалась линейная дискиминантная функция. Теперь рассмотрим ситуацию, когда матрицы ковариаций разных образов не совпадают. Для различных ковариационных матриц байесовский критерий предлагает строить квадратичную дискриминантную функцию. Однако, на практике ее строят чрезвычайно редко, поскольку никогда нельзя с точностью сказать равны или нет ковариационные матрицы. Мы ведь имеем только оценки, так как работаем не со всей генеральной совокупностью объектов, а только с выборкой из нее. Поэтому обычно вычисляют усредненную ковариационную матрицу для двух образов:
![]() ,
,
где
![]() – число объектов в 1-ой выборке;
– число объектов в 1-ой выборке;
![]() – число объектов
во 2-ой выборке;
– число объектов
во 2-ой выборке;
![]() – ковариационная
матрица для 1-го образа;
– ковариационная
матрица для 1-го образа;
![]() – ковариационная
матрица для 2-го образа.
– ковариационная
матрица для 2-го образа.
После этого применяется линейный дискриминантный анализ.
Распознавание с отказами.
Пусть имеется
![]() образов, где
образов, где
![]() (т.е.
известны эталоны для этих образов).
Тогда можно построить линейную
дискриминантную функцию для любой пары
образов:
(т.е.
известны эталоны для этих образов).
Тогда можно построить линейную
дискриминантную функцию для любой пары
образов:
![]() относится к i-му
образу, если
относится к i-му
образу, если
![]() для всех j, или к области
отказа, если такового i
– нет.
для всех j, или к области
отказа, если такового i
– нет.
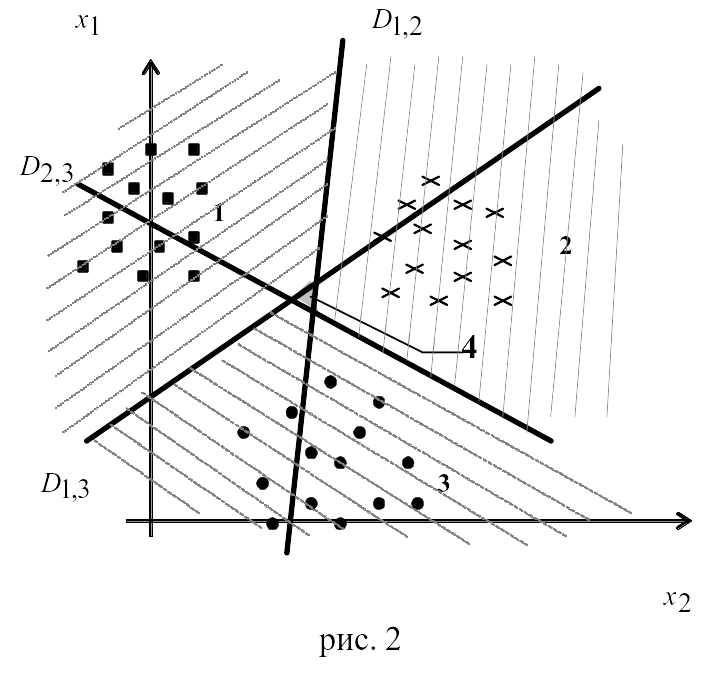
Посмотрим как это выглядит на графике (рис. 2), где
D – гиперплоскости;
1, 2, 3 – образы;
4 – область отказа.
В область отказа попадают такие точки, для которых невозможно определить принадлежность к одному из образов. Другими словами точка отказа – это такая точка, координаты которой при подстановке в дискриминантную функцию дают следующие значения:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Дискриминантный анализ эффективно использовать при достаточно близком расположении образов и даже при небольшом их наложении.
Практика показала, что дискриминантный анализ хорошо работает и для случая, когда нет многомерного нормального распределения. При этом необходимо, чтобы распределение по каждому образу было все таки симметрично и унимодально. Правда, при этом алгоритм уже нельзя рассматривать как статистический, а можно говорить об эвристическом алгоритме распознавания образов.
Практическая часть
Постановка задачи.
Исследуем, какие свойства относят квартиру к одной из трех категорий: (1) 1-комнатной, (2) 2-комнатной или (3) 3-комнатной.
В данной задаче имеются 3 образа: 1 – 1-комнатная квартира, 2 – 2-комнатная квартира и 3 – 3-комнатная квартира и 3 свойства: общая площадь, жилая площадь и цена квартиры.
Известна часть представителей каждого образа и значения их свойств (табл. 1). Требуется отнести квартиры (МЭ) к каждому из образов (табл. 2).
Исходные данные
|
Таблица 1.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Таблица 2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||