Файл: Курсовая Принятие решений на примере задачи распознавания образов с использованием алгоритма Дискриминантная функция.doc
ВУЗ: Государственный университет природы, общества и человека «Дубна»
Категория: Курсовая работа
Дисциплина: Методы оптимальных решений
Добавлен: 23.10.2018
Просмотров: 2077
Скачиваний: 46
На рис. 1 изображены объекты материала обучения и материала экзамена.
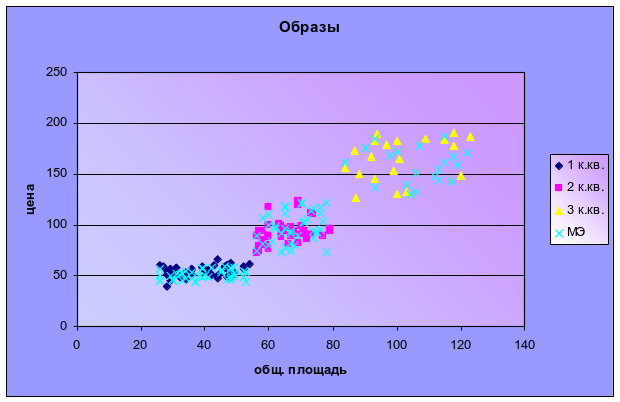 Рис.
1и 2 и между 2 и 3 образами.
Рис.
1и 2 и между 2 и 3 образами.
Решение
1. Вычисляем математическое ожидание для каждого свойства, каждого образа:
|
|
M1 |
M2 |
M3 |
|
средняя общ.пл. |
39,2 |
65,5 |
101,0 |
|
средняя цена |
54,7 |
93,3 |
165,3 |
|
средняя жил.пл. |
28,825 |
51,775 |
81,95 |
Мi – математическое ожидание для i-ого образа.
|
|
M1-M2 |
M2-M3 |
M1+M2 |
M2+M3 |
M1-M3 |
M1+M3 |
|
средняя общ.пл. |
-26,2 |
-35,5 |
104,7 |
166,5 |
-61,8 |
140,3 |
|
средняя цена |
-38,6 |
-72,0 |
148,0 |
258,6 |
-110,6 |
219,975 |
|
средняя жил.пл. |
-22,95 |
-30,175 |
80,6 |
133,725 |
-53,125 |
110,775 |
2. Построим матрицы ковариации:
Матрица ковариации для 1 образа:
|
65,39475831 |
15,45126111 |
63,50792818 |
|
15,45126111 |
28,769375 |
16,368125 |
|
63,50792818 |
16,368125 |
69,294375 |
Матрица ковариации для 2 образа:
|
40,699375 |
24,9575 |
36,981875 |
|
24,9575 |
125,71 |
6,9175 |
|
36,981875 |
6,9175 |
44,124375 |
Матрица ковариации для 3 образа:
|
141,1983988 |
88,92908133 |
156,9474912 |
|
88,92908133 |
419,11 |
93,565 |
|
156,9474912 |
93,565 |
190,4475 |
3. Вычислим среднюю и обратную матрицы ковариации:
Средняя матрица ковариации для 1 и 2 образов
|
45,17612916 |
20,20438055 |
50,24490159 |
|
20,20438055 |
77,2396875 |
11,6428125 |
|
50,24490159 |
11,6428125 |
56,709375 |
Обратная матрица ковариации 1 и 2 образов
|
-1,544008944 |
0,203987709 |
1,326122653 |
|
0,203987709 |
-0,013589793 |
-0,177944457 |
|
1,326122653 |
-0,177944457 |
-1,120786964 |
Средняя матрица ковариации для 2 и 3 образов
|
63,70446628 |
46,28136044 |
76,97041373 |
|
46,28136044 |
223,51 |
35,8 |
|
76,97041373 |
35,8 |
92,89875 |
Обратная матрица ковариации 2 и 3 образов
|
-0,721628727 |
0,057188283 |
0,575860506 |
|
0,057188283 |
0,000236293 |
-0,04747389 |
|
0,575860506 |
-0,04747389 |
-0,44806476 |
Средняя матрица ковариации для 1 и 3 образов
|
90,66263848 |
39,94386785 |
94,65444918 |
|
39,94386785 |
158,8829167 |
42,10041667 |
|
94,65444918 |
42,10041667 |
109,67875 |
Обратная матрица ковариации 1 и 3 образов
|
0,112573908 |
-0,002847867 |
-0,096059856 |
|
-0,002847867 |
0,007078644 |
-0,0002594 |
|
-0,096059856 |
-0,0002594 |
0,092118241 |
4. Вычислим коэффициенты b и p
Для образов 1 и 2:
|
b12 = |
|
p12 = |
-1351,05946 |
|||
|
|
|
|
|
Для образов 2 и 3:
|
b23 = |
|
p23 = |
-1527,631272 |
Для образов 1 и 3:
|
b13 = |
|
p13 = |
113,7887413 |
5. Вычисляем дискриминантную функцию и проводим распознавание.
В табл. 3 приведены результаты вычислений.
Таблица 3.
|
D(X)12 |
D(X)23 |
D(X)13 |
??? |
проверка на ошибки |
|
||
|
15,90745 |
39 |
7,287869449 |
1 |
13,0744164 |
33,53826 |
50,73509 |
1 |
|
16,75062 |
39 |
11,03023955 |
1 |
17,45029061 |
40,11716 |
63,08892 |
1 |
|
10,09422 |
32 |
0,58090434 |
1 |
13,92636333 |
36,36845 |
53,12999 |
1 |
|
12,14217 |
34 |
3,421415011 |
1 |
15,36800246 |
39,85175 |
62,72821 |
1 |
|
18,94339 |
38 |
8,999483204 |
1 |
12,29444218 |
34,82638 |
53,43849 |
1 |
|
21,17611 |
41 |
13,33863465 |
1 |
11,57203918 |
33,57286 |
53,73797 |
1 |
|
18,02225 |
39 |
8,970578034 |
1 |
13,21374159 |
35,46803 |
57,26919 |
1 |
|
18,6783 |
40 |
12,42249946 |
1 |
14,79042276 |
37,19706 |
58,15642 |
1 |
|
8,44274 |
30 |
-6,79003466 |
отказ |
14,34005576 |
38,47371 |
57,4872 |
1 |
|
19,04042 |
40 |
10,3718665 |
1 |
14,88928878 |
37,58034 |
55,72701 |
1 |
|
16,71994 |
37 |
5,906457589 |
1 |
10,52881313 |
35,17265 |
56,0626 |
1 |
|
15,95341 |
37 |
4,846007804 |
1 |
14,57079697 |
38,07897 |
56,54398 |
1 |
|
13,15472 |
31 |
-4,026999682 |
отказ |
6,785758599 |
31,06148 |
47,08482 |
1 |
|
14,08097 |
35 |
2,258012078 |
1 |
15,47286513 |
35,65972 |
51,48703 |
1 |
|
17,584 |
38 |
10,93288725 |
1 |
12,34039945 |
33,04194 |
50,99663 |
1 |
|
19,67557 |
40 |
12,53972837 |
1 |
22,91901356 |
41,09119 |
63,07269 |
1 |
|
17,07277 |
36 |
2,60969881 |
1 |
10,38387063 |
29,42478 |
40,6788 |
1 |
|
10,88348 |
33 |
-0,876374984 |
отказ |
4,55486254 |
27,26883 |
38,94388 |
1 |
|
12,85529 |
33 |
1,875811947 |
1 |
6,086084975 |
29,53793 |
44,86657 |
1 |
|
15,34149 |
35 |
2,754013405 |
1 |
17,60672787 |
37,95879 |
58,25559 |
1 |
|
16,63219 |
38 |
5,780200117 |
1 |
8,408397047 |
31,00607 |
45,53019 |
1 |
|
-13,1292 |
14 |
-40,48654224 |
2 |
12,81299728 |
32,73962 |
46,55453 |
1 |
|
12,06737 |
33 |
-3,06229397 |
отказ |
12,79771792 |
35,71745 |
54,12017 |
1 |
|
11,19402 |
31 |
-9,334849453 |
отказ |
17,14524546 |
38,74827 |
60,14203 |
1 |
|
15,37766 |
33 |
-3,52757064 |
отказ |
18,07749299 |
38,76678 |
57,61527 |
1 |
|
10,35748 |
32 |
0,959676757 |
1 |
11,35424609 |
33,34446 |
48,32374 |
1 |
|
14,18962 |
36 |
3,668329109 |
1 |
15,83131757 |
37,95195 |
57,03998 |
1 |
|
12,0692 |
32 |
-6,864082637 |
отказ |
5,735082539 |
29,95349 |
44,36154 |
1 |
|
12,14583 |
31 |
-4,182162324 |
отказ |
12,74197898 |
32,85414 |
48,69445 |
1 |
|
14,71795 |
34 |
0,624085274 |
1 |
19,72897665 |
41,01506 |
64,98621 |
1 |
|
17,584 |
38 |
10,93288725 |
1 |
6,797372555 |
30,30428 |
47,12276 |
1 |
|
14,96776 |
36 |
4,766712626 |
1 |
8,880243344 |
32,11752 |
49,72917 |
1 |
|
11,37747 |
32 |
-1,440823442 |
отказ |
8,362205058 |
31,97352 |
48,98492 |
1 |
|
8,223613 |
30 |
-5,808880054 |
отказ |
11,35607879 |
32,23415 |
44,52195 |
1 |
|
21,3191 |
41 |
12,2691563 |
1 |
7,784860076 |
30,13582 |
43,40026 |
1 |
|
13,33767 |
33 |
1,273429757 |
1 |
8,858265504 |
30,97379 |
43,60582 |
1 |
|
7,960361 |
30 |
-6,18765247 |
отказ |
13,46904487 |
33,69294 |
50,00645 |
1 |
|
8,738503 |
30 |
-5,089268953 |
отказ |
17,43305935 |
37,05626 |
54,20129 |
1 |
|
10,31518 |
31 |
-4,202038933 |
отказ |
13,08553181 |
34,02543 |
48,17943 |
1 |
|
8,694378 |
30 |
-6,449195976 |
отказ |
5,811219192 |
30,6068 |
44,44987 |
1 |
|
-13,1101 |
16 |
-35,40069402 |
2 |
0,176657083 |
23,04462 |
27,79824 |
1 |
|
-22,5281 |
10 |
-49,7385334 |
2 |
-3,152705018 |
21,03872 |
23,17767 |
2 |
|
-20,3348 |
9 |
-49,17569317 |
2 |
-4,258621066 |
20,11768 |
21,65012 |
2 |
|
-15,6154 |
12 |
-41,3647437 |
2 |
-6,05492803 |
19,27057 |
19,15045 |
2 |
|
8,583898 |
31 |
-4,057724339 |
отказ |
-8,93392313 |
15,98801 |
15,1991 |
2 |
|
-8,00301 |
16 |
-30,77270213 |
2 |
-4,174535862 |
22,23441 |
29,37996 |
2 |
|
-25,9317 |
6 |
-58,24921737 |
2 |
-9,944638563 |
17,67087 |
18,84573 |
2 |
|
-26,9745 |
7 |
-53,33098806 |
2 |
-14,13756155 |
13,59199 |
11,79232 |
2 |
|
-25,5844 |
8 |
-50,14061014 |
2 |
-7,797827708 |
19,3468 |
19,25683 |
2 |
|
-12,6714 |
16 |
-34,76940666 |
2 |
-13,8557443 |
16,47528 |
14,66335 |
2 |
|
-1,10476 |
22 |
-23,82225064 |
2 |
-9,300204926 |
19,3814 |
22,25972 |
2 |
|
-5,72665 |
19 |
-27,66722024 |
2 |
-13,57904582 |
14,29609 |
11,27826 |
2 |
|
-16,5783 |
11 |
-43,96176799 |
2 |
-13,64589976 |
15,24026 |
12,43607 |
2 |
|
-7,88508 |
18 |
-28,11625927 |
2 |
-7,490451304 |
18,361 |
20,99553 |
2 |
|
-15,6706 |
12 |
-40,16900788 |
2 |
-3,446017023 |
26,06167 |
40,52378 |
2 |
|
-18,3003 |
12 |
-42,57132757 |
2 |
-11,53293369 |
16,69905 |
17,92056 |
2 |
|
-26,0766 |
8 |
-53,37795035 |
2 |
-13,27216796 |
14,55466 |
10,42337 |
2 |
|
-11,3672 |
16 |
-35,50707488 |
2 |
-14,88319245 |
13,85287 |
12,01593 |
2 |
|
-18,4396 |
10 |
-49,10542656 |
2 |
-12,86959094 |
16,17276 |
17,33624 |
2 |
|
-13,8214 |
15 |
-37,65687962 |
2 |
-12,27489919 |
14,73931 |
10,5406 |
2 |
|
-7,97283 |
18 |
-28,24251674 |
2 |
-11,80546822 |
15,41324 |
16,29567 |
2 |
|
-13,3404 |
15 |
-31,86387657 |
2 |
-14,2118655 |
11,82837 |
7,902211 |
2 |
|
-22,8104 |
9 |
-55,20315405 |
2 |
-8,587084644 |
19,03744 |
20,71411 |
2 |
|
-15,738 |
15 |
-41,60480237 |
2 |
-14,50017794 |
14,76475 |
11,24936 |
2 |
|
-20,2053 |
10 |
-46,48131658 |
2 |
-13,26238671 |
14,90777 |
14,26309 |
2 |
|
-29,2188 |
5 |
-57,70807323 |
2 |
-17,73762548 |
9,189969 |
1,745065 |
2 |
|
-3,25157 |
21 |
-24,23335594 |
2 |
-15,37718549 |
14,55929 |
12,58038 |
2 |
|
-15,3846 |
12 |
-42,30796458 |
2 |
-11,93734341 |
16,19126 |
14,80948 |
2 |
|
-4,41089 |
19 |
-28,36695473 |
2 |
-10,04217042 |
17,42166 |
14,87975 |
2 |
|
-24,1048 |
8 |
-50,62576342 |
2 |
-14,30011465 |
13,17663 |
5,182357 |
2 |
|
-20,2494 |
11 |
-47,84124361 |
2 |
-9,702781945 |
17,7633 |
15,34684 |
2 |
|
-50,3938 |
-13 |
-93,34141257 |
3 |
-22,73558331 |
9,023925 |
1,120986 |
2 |
|
-4,31203 |
19 |
-30,7963601 |
2 |
-20,54331372 |
10,15978 |
-3,50337 |
2 |
|
-13,6686 |
16 |
-34,88663557 |
2 |
-22,67851062 |
7,726651 |
-3,87654 |
2 |
|
-4,77534 |
21 |
-25,10812968 |
2 |
-23,88012583 |
5,446087 |
-13,1719 |
2 |
|
-17,8393 |
12 |
-47,05136589 |
2 |
-14,17007217 |
13,50892 |
10,47033 |
2 |
|
-23,8397 |
7 |
-54,04877967 |
2 |
-16,39351822 |
12,42405 |
7,377304 |
2 |
|
-7,65484 |
19 |
-31,65307672 |
2 |
-9,443195523 |
19,67225 |
23,32919 |
2 |
|
-13,8557 |
16 |
-35,17708424 |
2 |
-17,3123191 |
10,53803 |
6,140207 |
2 |
|
-11,6397 |
15 |
-37,13197312 |
2 |
-25,59051488 |
5,605392 |
-11,7435 |
2 |
|
-54,335 |
-17 |
-100,0539785 |
3 |
-38,95854078 |
-6,94062 |
-31,4464 |
3 |
|
-62,2659 |
-20 |
-109,8290567 |
3 |
-54,00494366 |
-17,9999 |
-50,9926 |
3 |
|
-60,9334 |
-16 |
-104,2347509 |
3 |
-42,5992925 |
-9,43309 |
-44,3488 |
3 |
|
-42,7053 |
-9 |
-82,66104726 |
3 |
-42,98538315 |
-8,10082 |
-37,0416 |
3 |
|
-55,7961 |
-14 |
-97,0765736 |
3 |
-52,32333122 |
-13,8275 |
-55,0241 |
3 |
|
-50,7099 |
-15 |
-93,73264127 |
3 |
-54,24779736 |
-15,6036 |
-52,6809 |
3 |
|
-40,8881 |
-7 |
-78,87731572 |
3 |
-32,4071297 |
-3,53114 |
-30,011 |
3 |
|
-68,8253 |
-25 |
-118,9060086 |
3 |
-62,05828766 |
-18,7084 |
-63,1421 |
3 |
|
-61,7278 |
-21 |
-109,0335781 |
3 |
-45,48522567 |
-5,88932 |
-32,9311 |
3 |
|
-58,2229 |
-19 |
-104,1604916 |
3 |
-71,26600842 |
-27,3021 |
-74,9792 |
3 |
|
-57,7178 |
-20 |
-107,2806029 |
3 |
-62,16887487 |
-18,378 |
-58,6162 |
3 |
|
-44,8201 |
-9 |
-84,34375584 |
3 |
-58,39673082 |
-18,2948 |
-61,9798 |
3 |
|
-57,6133 |
-15 |
-100,8603051 |
3 |
-65,85619087 |
-23,9205 |
-66,1962 |
3 |
|
-64,2238 |
-24 |
-113,751502 |
3 |
-67,11487877 |
-24,9038 |
-70,494 |
3 |
|
-51,0057 |
-15 |
-95,43340697 |
3 |
-71,54037566 |
-27,4776 |
-72,8023 |
3 |
|
-7,21792 |
20 |
-27,22000069 |
2 |
-58,93704463 |
-16,6213 |
-57,9617 |
3 |
|
-48,9216 |
-16 |
-98,87448035 |
3 |
-52,19056982 |
-12,7134 |
-48,5942 |
3 |
|
-48,0547 |
-7 |
-86,38375201 |
3 |
-48,72749983 |
-12,5959 |
-46,2893 |
3 |
|
-55,499 |
-14 |
-101,7711931 |
3 |
-66,36363056 |
-21,3466 |
-61,8679 |
3 |
|
-39,1438 |
-7 |
-85,37908182 |
3 |
-42,68986216 |
-4,65995 |
-20,1312 |
3 |
|
1св-во (рис.2) |
|
|
|
|
1 2 |
x |
y |
z |
|
|
26 |
-2,887527939 |
40 |
|
|
79 |
153,4694571 |
40 |
|
2 3 |
x |
y |
z |
|
|
56 |
99,46503296 |
40 |
|
|
123 |
550,6700441 |
40 |
|
1 3 |
x |
y |
z |
|
|
26 |
196,5386786 |
40 |
|
|
123 |
-246,4289809 |
40 |
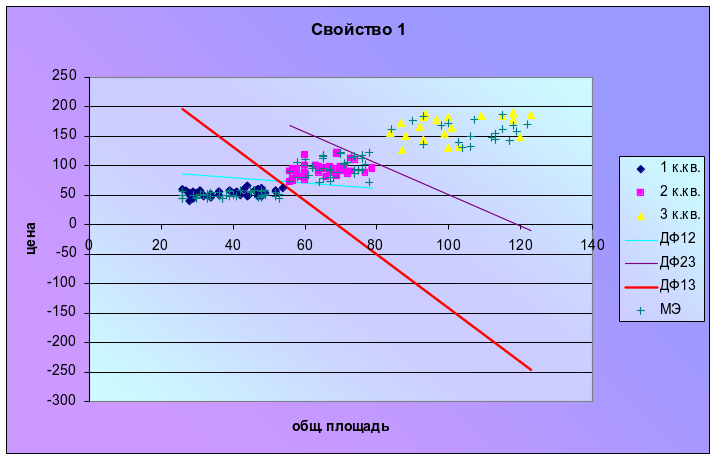
Рис.2.
|
2св-во (рис.3) |
|
|
|
|
|
|
|
|
|
1 2 |
x |
y |
z |
|
|
40 |
38,41431716 |
40 |
|
|
123 |
283,275256 |
40 |
|
2 3 |
x |
y |
z |
|
|
72 |
207,2154834 |
40 |
|
|
191 |
1008,609458 |
40 |
|
1 3 |
x |
y |
z |
|
|
40 |
160,2836664 |
40 |
|
|
191 |
-230,7525366 |
40 |
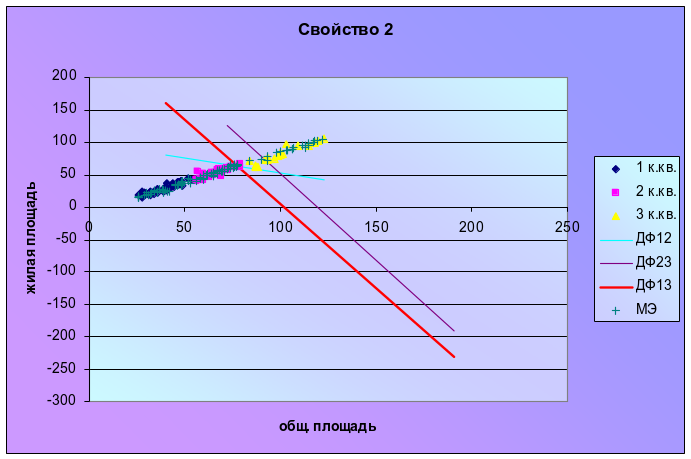
Рис.3
|
3св-во (рис.4) |
|
|
|
|
1 2 |
x |
y |
z |
|
|
15 |
-35,33897766 |
40 |
|
|
65 |
112,167612 |
40 |
|
2 3 |
x |
y |
z |
|
|
40 |
-8,285417474 |
40 |
|
|
106 |
436,1851906 |
40 |
|
1 3 |
x |
y |
z |
|
|
15 |
225,0247596 |
40 |
|
|
106 |
-10,63281965 |
40 |
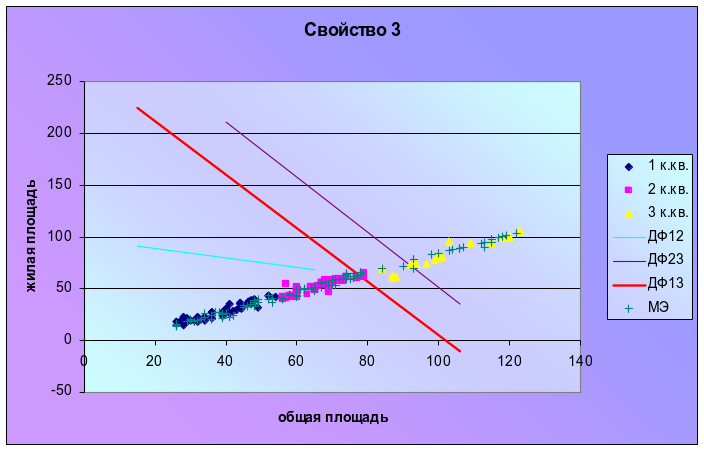
Рис.4.
Заключение
Дискриминантный анализ эффективно использовать при достаточно близком расположении образов и даже при небольшом их наложении и когда в материале обучения присутствует 2 и более образов.
Для решения данной задачи использовался алгоритм «Дискриминантная функция», т.к. в материале обучения присутствует 3 образа и объекты обучения имеют нормальное распределение, т.е. образы компактны.
В результате для данной задачи распознавание с помощью алгоритма «Дискриминантная функция» дало ошибку 1-го и 2-го рода и область отказа. Объекты материала экзамены были полностью распознаны.
Список литературы
-
Вапник В.Н., Червоненскис А.Я. Теория распознавания образов. – М. 1974.
-
Васотев В.И. Распознавательные системы. – Киев. 1969.
-
Горелик А.Л., Скрипкин В.А. Методы распознавания образов. – М. 1977.
-
Добрынин В.Н., Черемисина Е.Н., Булякова И.А и др. Математические методы системного анализа и теория принятия решений. – Дубна. 2002.
-
Черемисина Е.Н. Конспект лекций по ТПР.