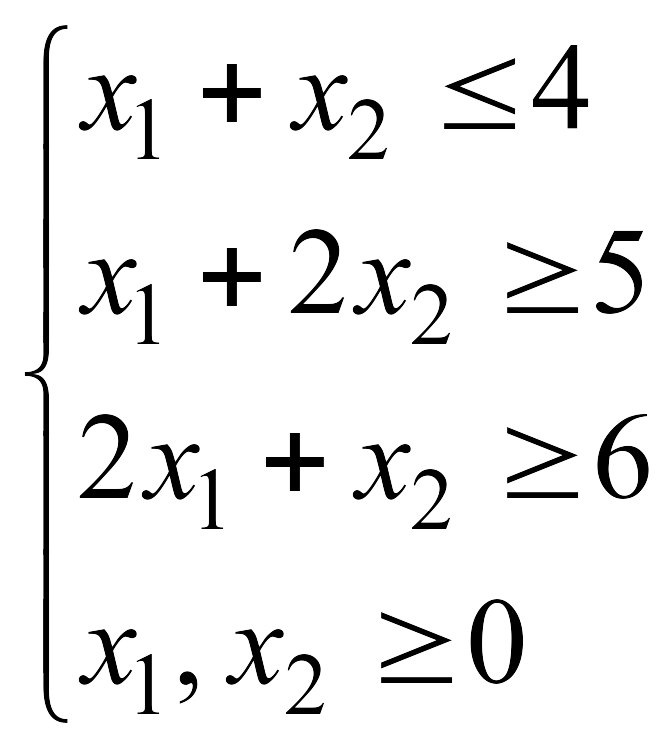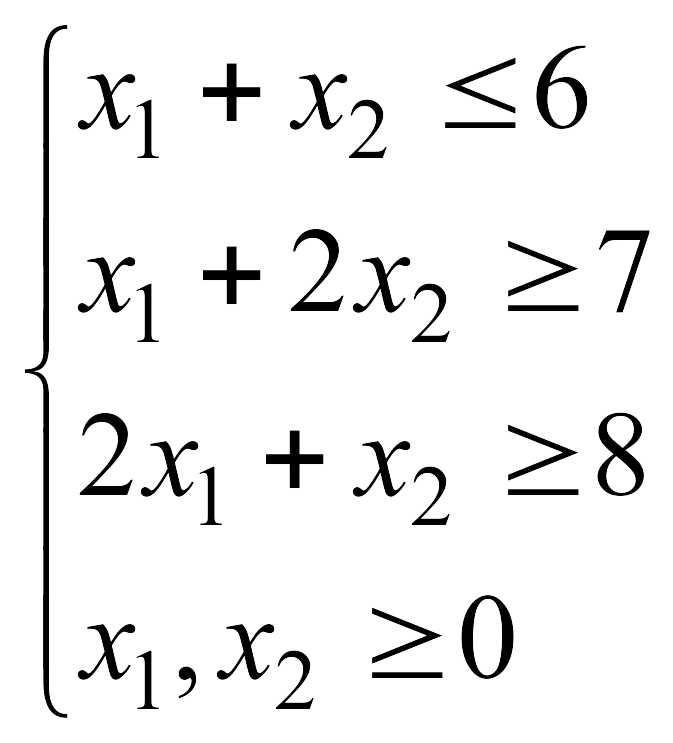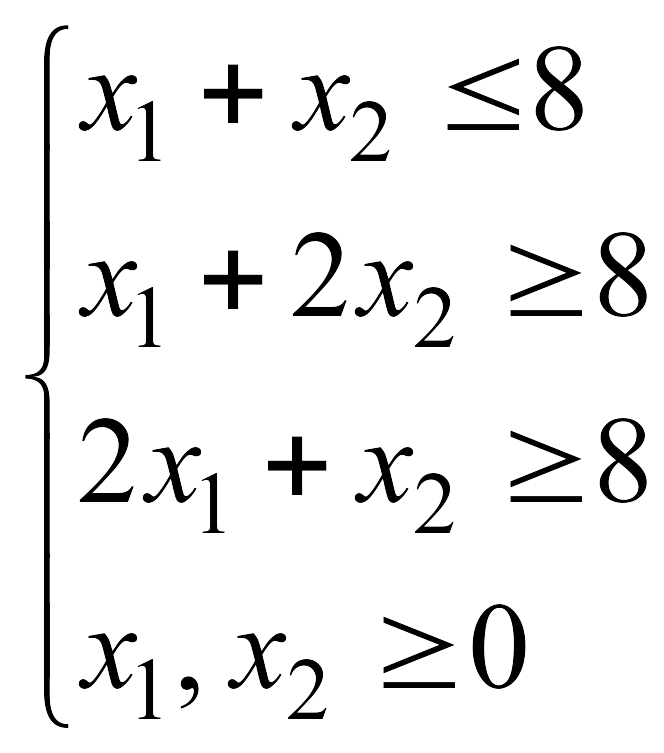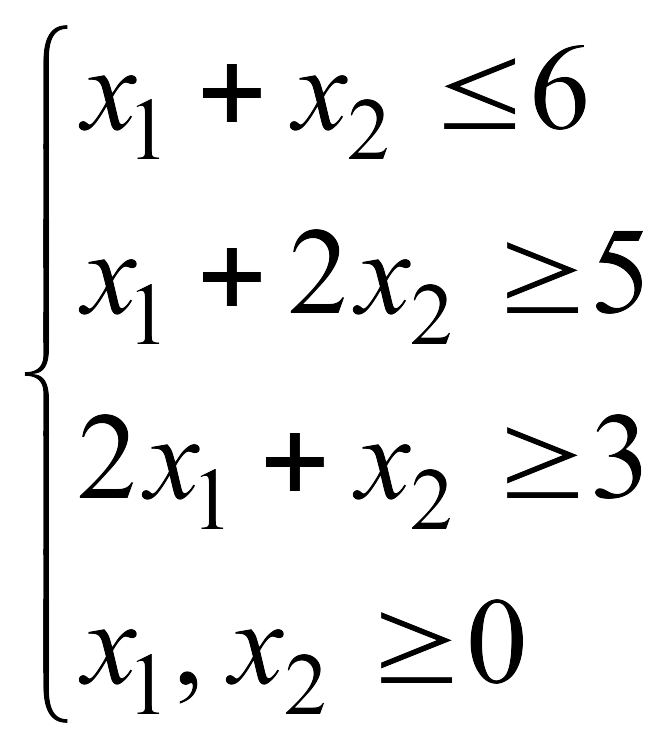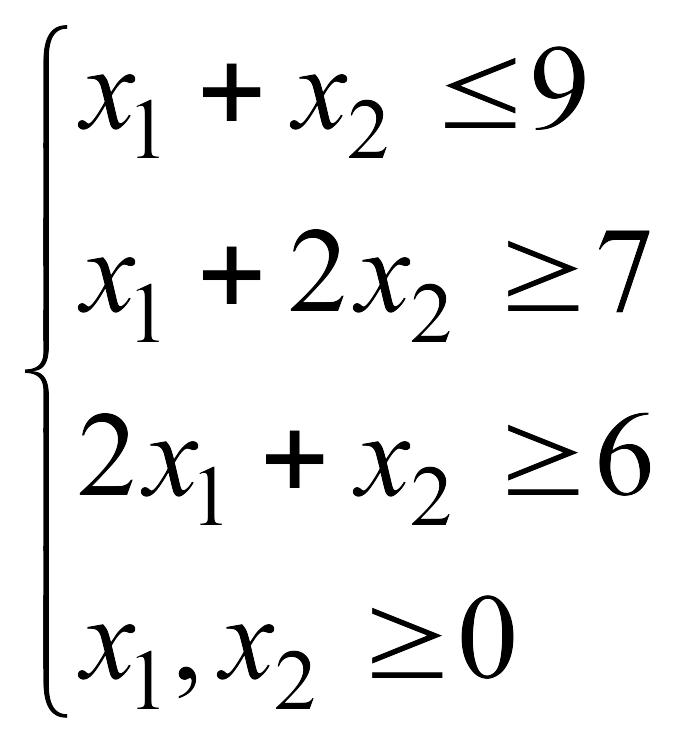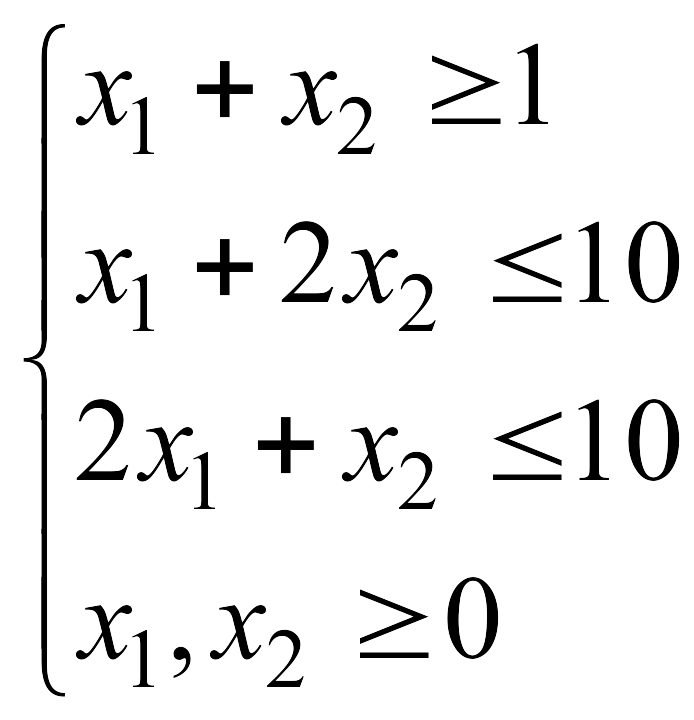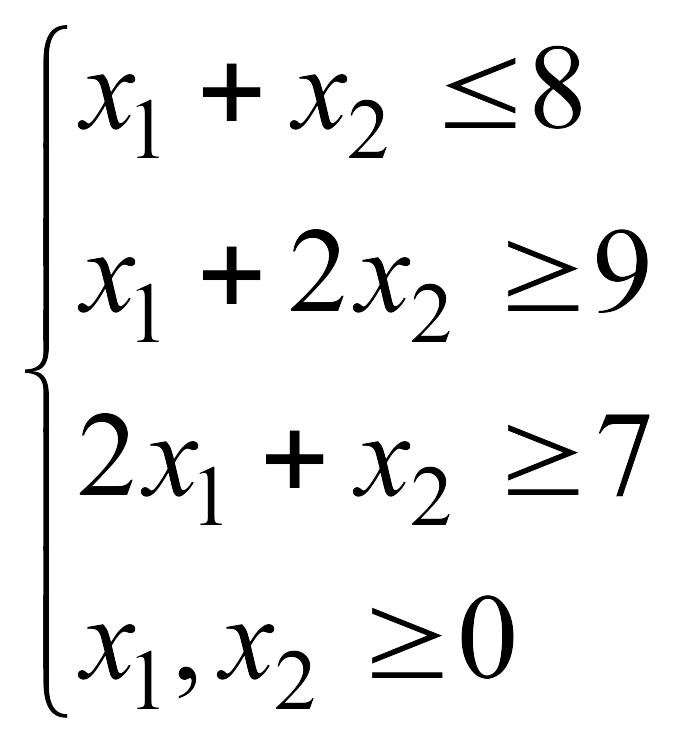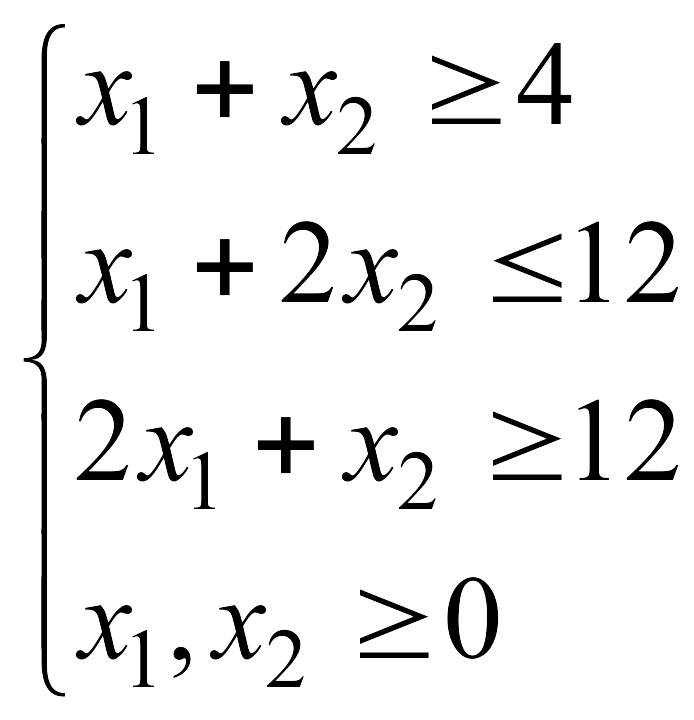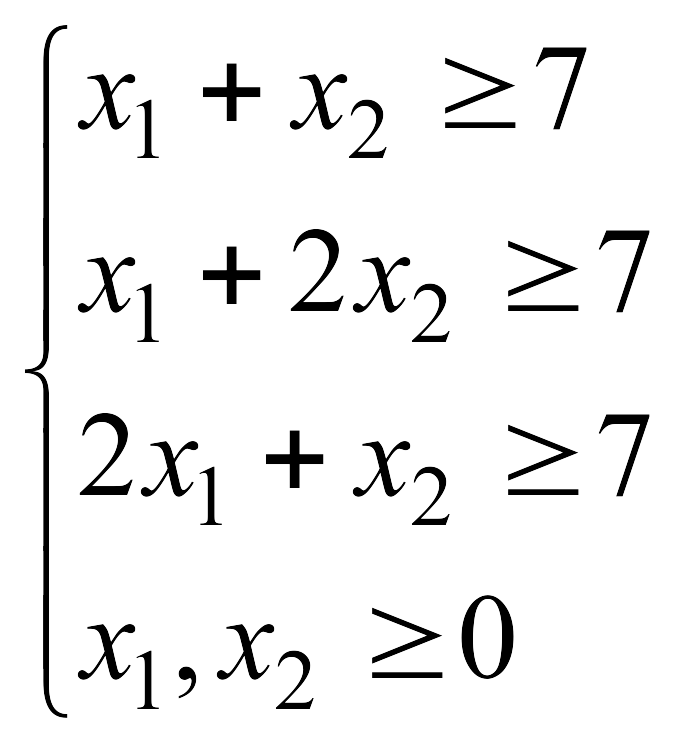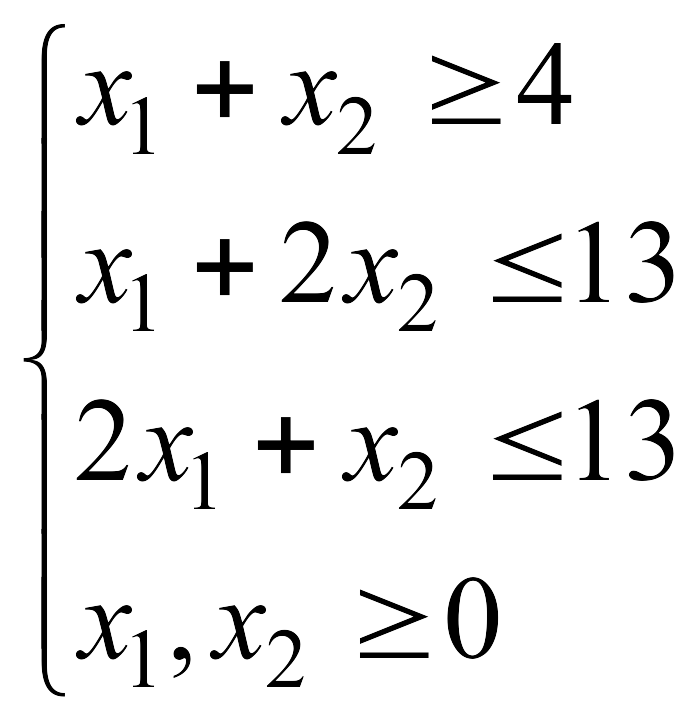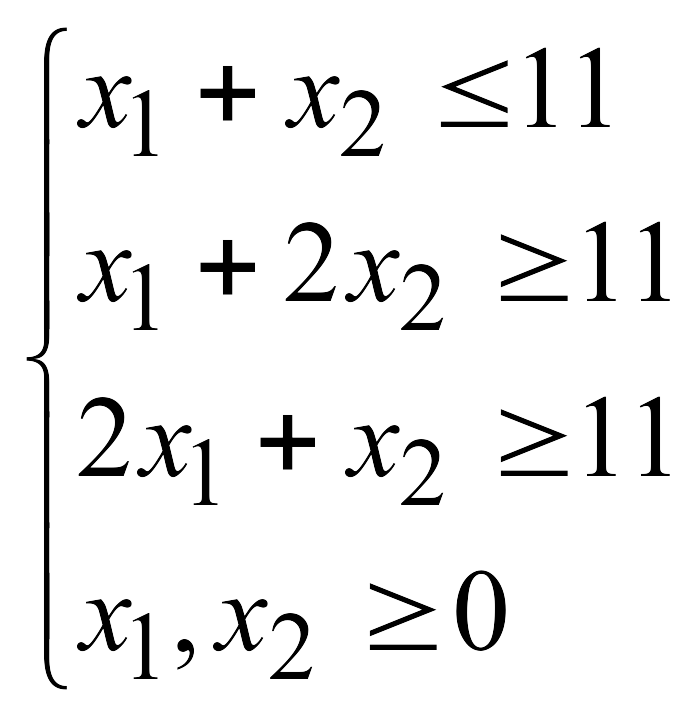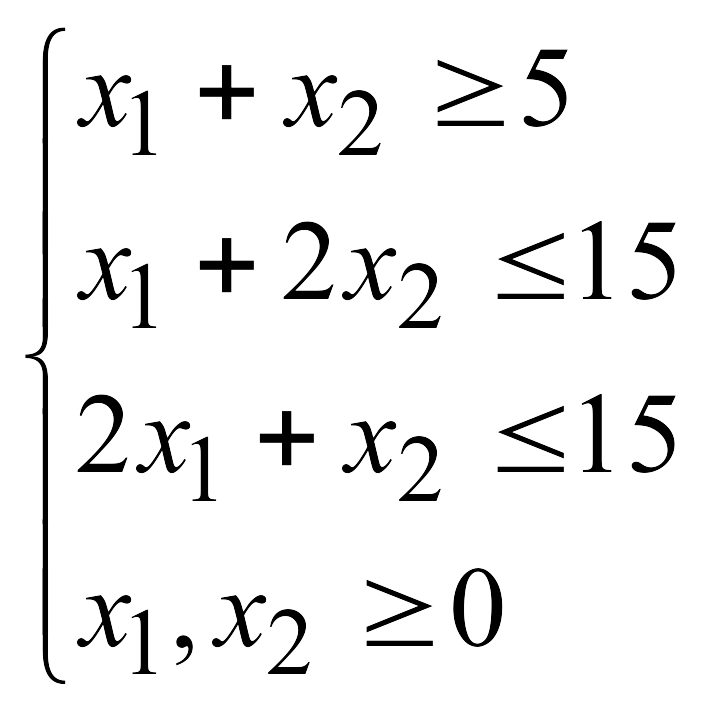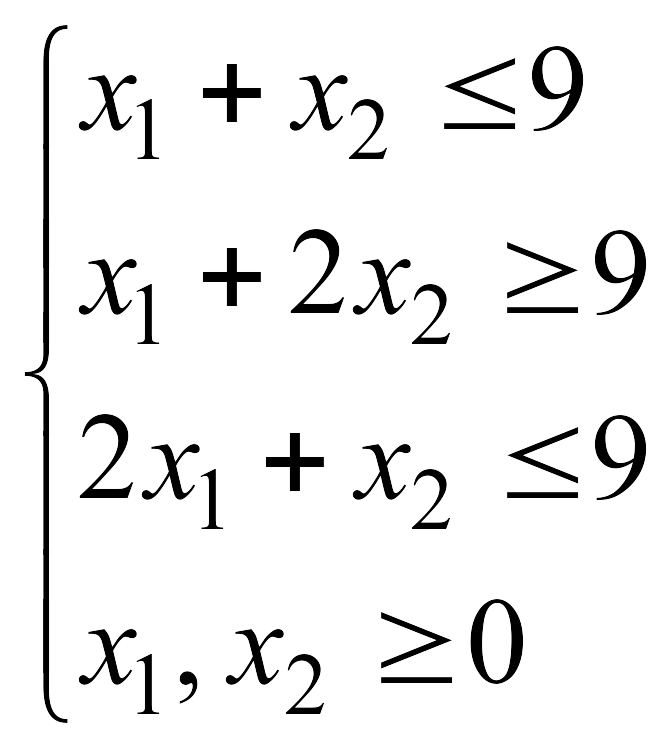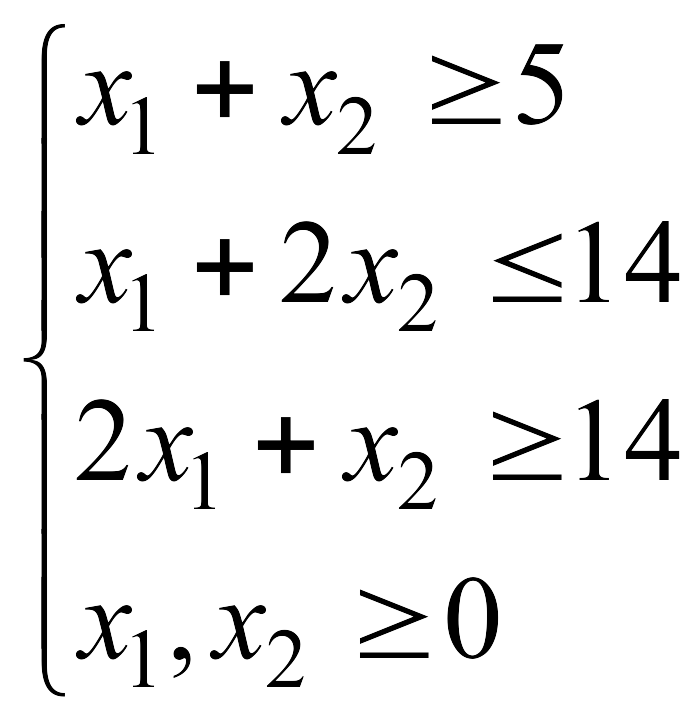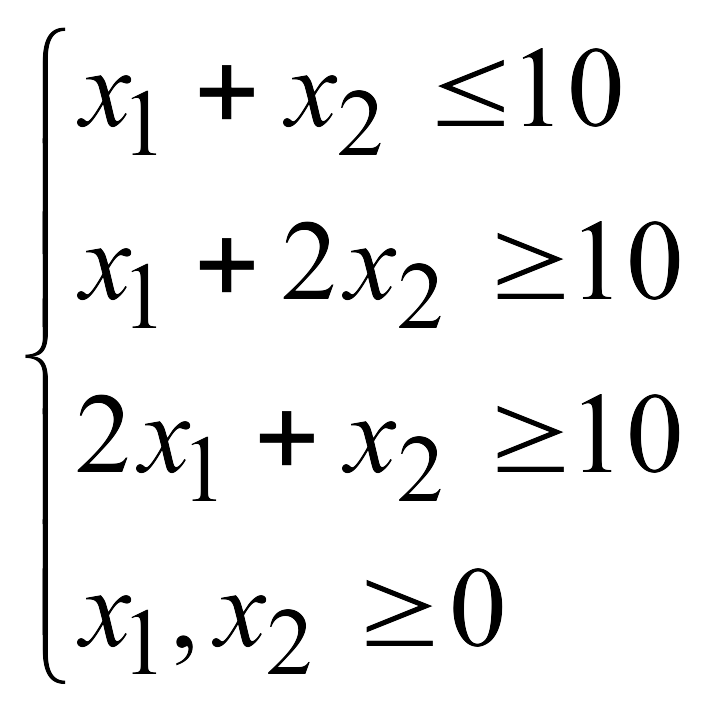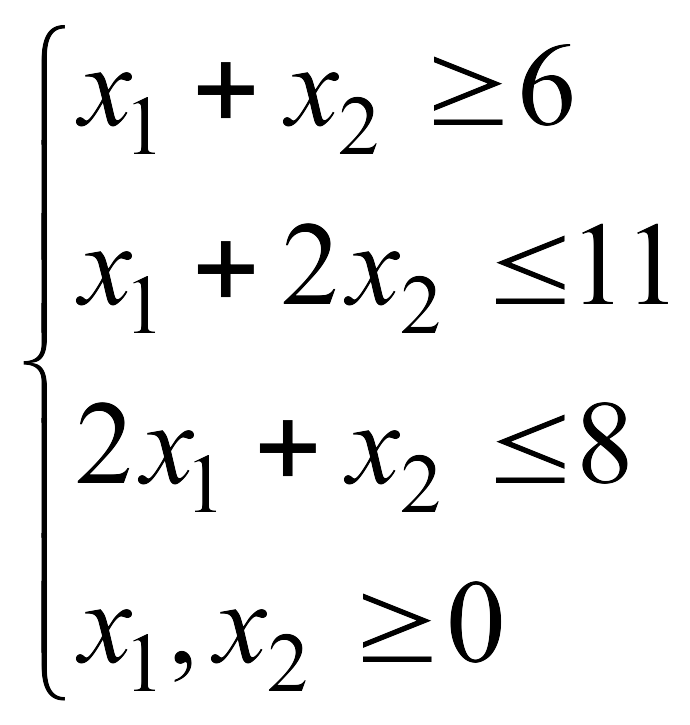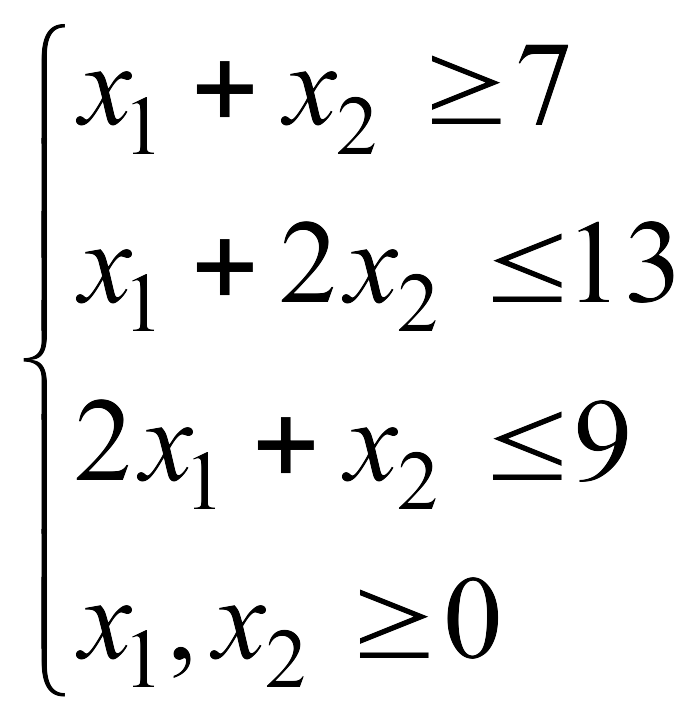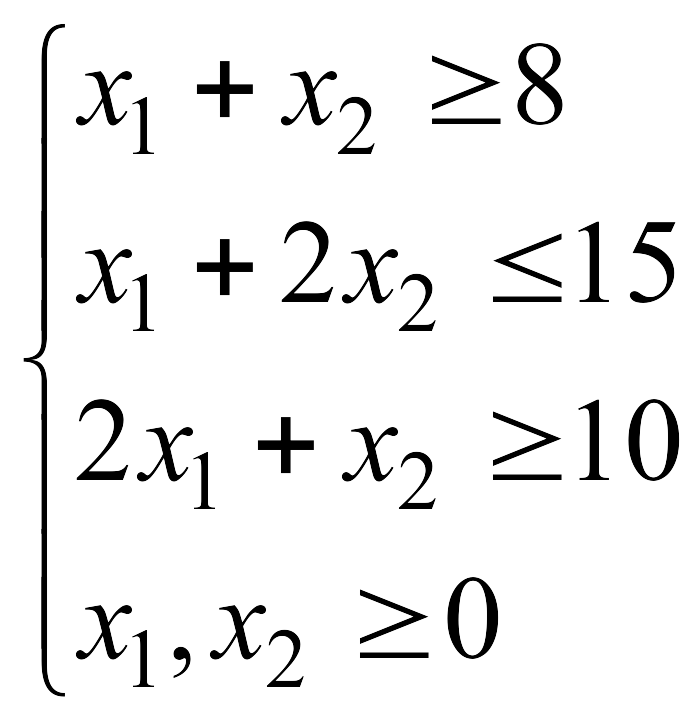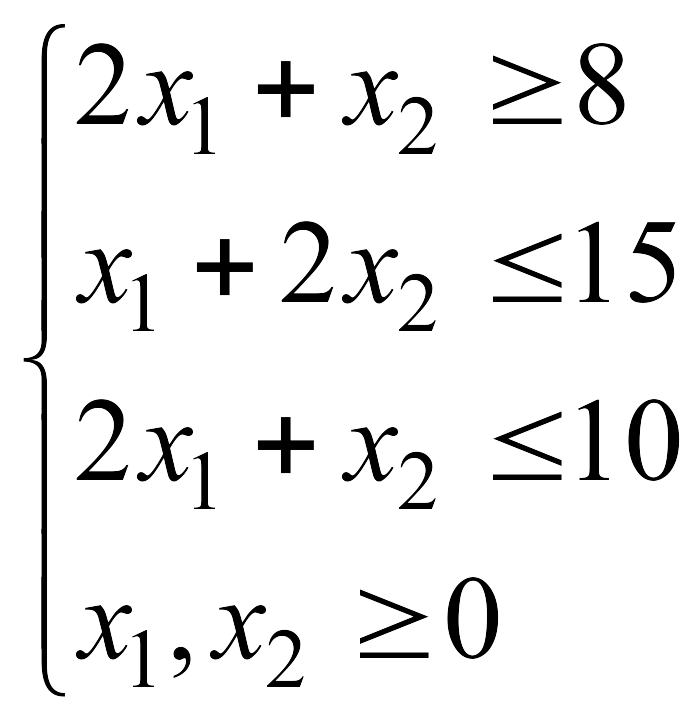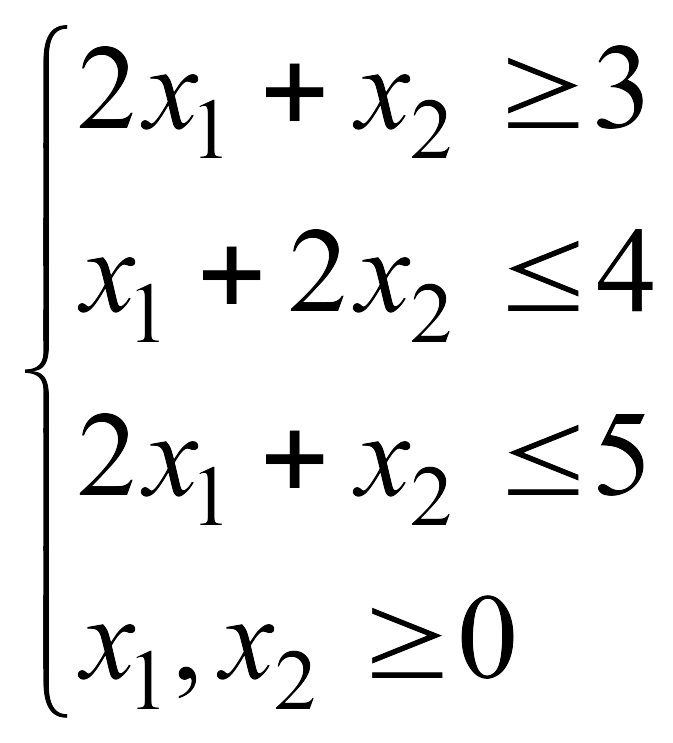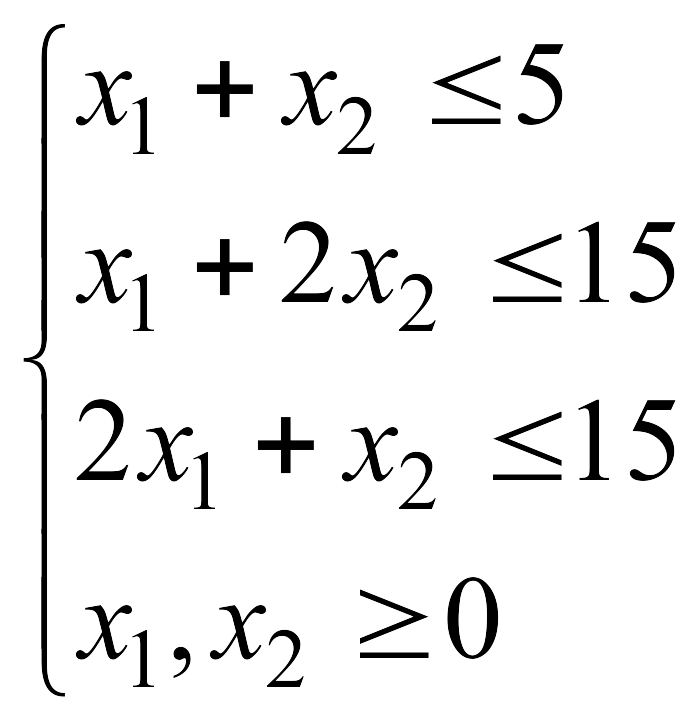Министерство образования и науки

Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

Национальный исследовательский ядерный университет «МИФИ»

Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению индивидуального домашнего задания (контрольной работы)

по курсу

«линейное программирование»

для студентов специальности 230201

«Информационные системы и технологии»

всех форм обучения

Волгодонск

2010

УДК 519.8 (075.8)

Рецензент д.т.н., профессор А. В. Чернов

Составитель ст. преп. Цуверкалова О.Ф.

Метод. указ. к выполнению индивидуального домашнего задания (контрольной работы) по дисциплине «Линейное программирование» /ВИТИ НИЯУ МИФИ. Волгодонск, 2010. 52 с.

Предназначены для студентов очной, очно-заочной и заочной формы обучения специальности 230201 – Информационные системы и технологии

ã ВИТИ НИЯУ МИФИ, 2010

• О.Ф. Цуверкалова, 2010

---

Методические указания

Целью выполнения индивидуального домашнего задания (контрольной работы) по курсу «Линейное программирование» является совершенствование навыков построения математических моделей и решения линейных оптимизационных задач с ограничениями.

Перед выполнением заданий студент должен ознакомиться с соответствующими теоретическими разделами курса и ответить на вопросы для самоконтроля, помещенные в конце каждой задачи.

Первая часть задания включает в себя задачи 1-3 и посвящена прямой и двойственной задаче линейного программирования (ЗЛП).

Задача 1 заключается в отыскании минимума линейной функции двух переменных в замкнутой области геометрическим путем. При решении в первую очередь необходимо построить область допустимых значений переменных, заданную системой неравенств. Направление роста целевой функции определяется вектором-градиентом, координаты которого равны коэффициентам при неизвестных в целевой функции. Для получения оптимального решения следует построить вектор-градиент, провести какую-либо линию уровня целевой функции перпендикулярно градиенту и перемещать ее в направлении антиградиента до достижения точки минимума.

В задаче 2 требуется построить математическую модель задачи максимизации прибыли производственного предприятия и определить максимальный план производства, а также сформулировать и решить двойственную задачу. Следует обратить внимание на экономический смысл задач и входящих в них переменных. В конце решения следует дать экономическую интерпретацию результатов.

Задача 3 посвящена применению метода искусственного базиса для отыскания начального допустимого решения ЗЛП. При решении задачи необходимо сформулировать вспомогательную ЗЛП и решить ее симплекс-методом, последовательно исключая искусственные переменные. Если минимум вспомогательной целевой функции равен 0, то найденное решение следует принять за начальный план исходной задачи, проверить его оптимальность и, если необходимо, продолжить решение симплекс-методом.

Вторая часть задания состоит из задач 4-7 и посвящена частным случаям ЗЛП (целочисленное программирование и транспортная задача), а также основам матричной теории игр и применению линейного программирования для отыскания оптимальных стратегий матричной игры.

Задача 4 посвящена решению целочисленной задачи линейного программирования методом Гомори, заключающимся в последовательном отсечении нецелочисленных оптимальных решений. Если задача допускает геометрическую интерпретацию, то следует графически показать ход решения.

Задача 5 рассматривает частный случай ЗЛП – транспортную задачу по критерию стоимости. Перед началом решения следует проверить, является ли модель задачи закрытой. Если нет, то следует преобразовать ее в закрытую путем введения фиктивного поставщика (потребителя). Начальное распределение поставок проводится методами северо-западного угла и наименьших затрат. Оптимизировать следует распределение, полученное методом северо-западного угла. В конце решения необходимо определить, является ли найденный оптимальный план единственным, и пояснить, почему.

---

Задача 6 предназначена для знакомства с основными понятиями матричной теории игр и минимаксными чистыми стратегиями.

Задача 7 ориентирована на отыскание оптимальной смешанной стратегии игры путем сведения ее к задаче линейного программирования. Перед началом решения следует выполнить упрощение игры путем отбрасывания заведомо невыгодных стратегий, если это возможно. Найденное решение необходимо сравнить с решением, полученным графическим путем.

Выбор варианта задания осуществляется в соответствии с порядковым номером студента по журналу (для студентов дневной формы обучения) или по номеру зачетки в соответствии с Приложением 1 (для студентов очно-заочной и заочной форм обучения).

Требования к оформлению. Отчеты по задачам должны быть выполнены с соблюдением всех требований, предъявляемых к оформлению документов в учебном процессе. Все расчеты должны быть выполнены без округлений, дробные результаты – представлены в обыкновенных дробях. При нахождении решения геометрическим методом все графики должны быть выполнены с соблюдением масштаба.

Рекомендуемая литература:

1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высш. шк., 1986.

2. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Исследование операций в экономике. – М.: ЮНИТИ, 2000. – 407 с.

3. Кузнецов А.В., Сакович В.А., Холод Н.И.. Высшая математика: Математическое программирование. – Мн.: Выш. шк., 1994. - 286 с.

4. Морозов В.В., Сухарев А.Г., Федоров В.В. Исследование операций в задачах и упражнениях. – М.: Высш. шк., 1986. – 287 с.

5. Цуверкалова О.Ф. Курс лекций по дисциплине «Линейное программирование».

Задача 1

Решить графически ЗЛП при указанных ограничениях:

№			Ограничения		№			Ограничения
1.	3	2			8.	3	2
2.	3	2			9.	3	2
3.	3	2			10.	2	5
4.	3	2			11.	2	5
5.	3	2			12.	2	5
6.	3	2			13.	2	5
7.	3	2			14.	2	5

№			Ограничения		№			Ограничения
15.	3	2			23.	2	5
16.	2	5			24.	4	-1
17.	2	5			25.	4	-1
18.	2	5			26.	4	-1
19.	2	5			27.	4	-1
20.	4	-1			28.	4	-1
21.	4	-1			29.	4	-1
22.	4	-1			30.	4	-1

Образец выполнения задачи 1.

---

Решим графически следующую ЗЛП:

Построим область допустимых значений – четырехугольник ABCD (рис.1).

Координаты вектор-градиента равны коэффициентам целевой функции:

.

Проведём через область ABCD произвольную линию уровня перпендикулярно направлению градиента – прямая (4).

Поскольку задача решается на максимум, перемещаем линию уровня (4) в направлении возрастания целевой функции, т.е. в направлении градиента. (Если задача решается на минимум, линия уровня перемещается в направлении антиградиента.)

Предельное положение – линия (5). Следовательно, точка D является оптимальным решением, обеспечивающим максимальное значение целевой функции.

Рисунок 1 – Графическое решение ЗЛП.

Определим координаты точки D как пересечение прямых (1) и (3):

Оптимальное решение:

,

.

Вопросы для самопроверки:

1. Как определить какая из полуплоскостей удовлетворяет заданному ограничению?

2. Какой вид может иметь область допустимых значений?

3. В каком случае ЗЛП имеет бесконечное множество решений? Не имеет решений?

4. В каком случае ЗЛП можно решить графически?

5. Как свести многомерную ЗЛП к графическому решению?

---

Задача 2

Предприятие производит три вида продукции А₁, А₂, А₃, используя сырье двух видов В₁, В₂. Затраты a_ij сырья i-го вида на единицу продукции j-го вида и запасы сырья i-го вида b_i, а также прибыль c_j, получаемая от продажи единицы продукции j-го вида, приведены в таблице. Определить план производства изделий, при котором суммарная прибыль будет максимальной.

Решить задачу симплекс-методом. Составить двойственную задачу и решить ее симплекс-методом. Показать взаимосвязь между двойственными задачами. Одну из двойственных задач решить графическим методом.

1.

Вид сырья	Расход сырья на единицу продукции			Общий запас сырья
	А1	А2	А3
В1	1	2	2	1100
В2	3	4	2	1500
Прибыль на единицу продукции	2	1	3

2.

Вид сырья	Расход сырья на единицу продукции			Общий запас сырья
	А1	А2	А3
В1	2	3	4	1200
В2	3	1	2	1600
Прибыль на единицу продукции	2	1	3

3.

Вид сырья	Расход сырья на единицу продукции			Общий запас сырья
	А1	А2	А3
В1	1	2	1	1000
В2	3	5	2	1500
Прибыль на единицу продукции	2	1	3

4.

Вид сырья	Расход сырья на единицу продукции			Общий запас сырья
	А1	А2	А3
В1	2	1	4	1600
В2	2	1	3	1800
Прибыль на единицу продукции	2	1	3

5.

Вид сырья	Расход сырья на единицу продукции			Общий запас сырья
	А1	А2	А3
В1	4	1	3	1500
В2	4	2	1	2000
Прибыль на единицу продукции	2	1	3

6.

Вид сырья	Расход сырья на единицу продукции			Общий запас сырья
	А1	А2	А3
В1	2	1	1	800
В2	2	3	2	1200
Прибыль на единицу продукции	3	3	3

7.

Вид сырья	Расход сырья на единицу продукции			Общий запас сырья
	А1	А2	А3
В1	3	1	2	900
В2	1	2	3	1000
Прибыль на единицу продукции	3	3	2

8.

Вид сырья	Расход сырья на единицу продукции			Общий запас сырья
	А1	А2	А3
В1	3	1	1	1800
В2	2	3	1	2400
Прибыль на единицу продукции	3	3	2

9.

Вид сырья	Расход сырья на единицу продукции			Общий запас сырья
	А1	А2	А3
В1	2	2	1	1300
В2	3	2	2	900
Прибыль на единицу продукции	3	3	2

---