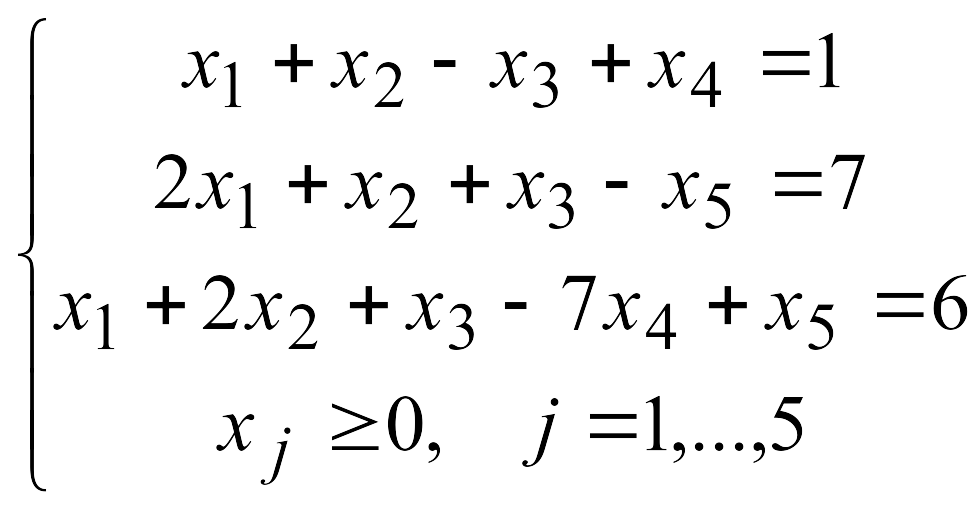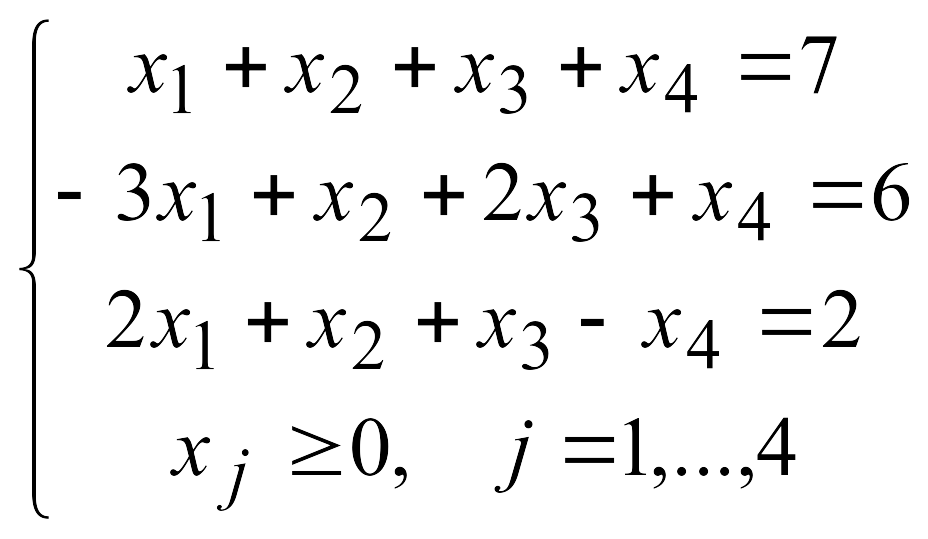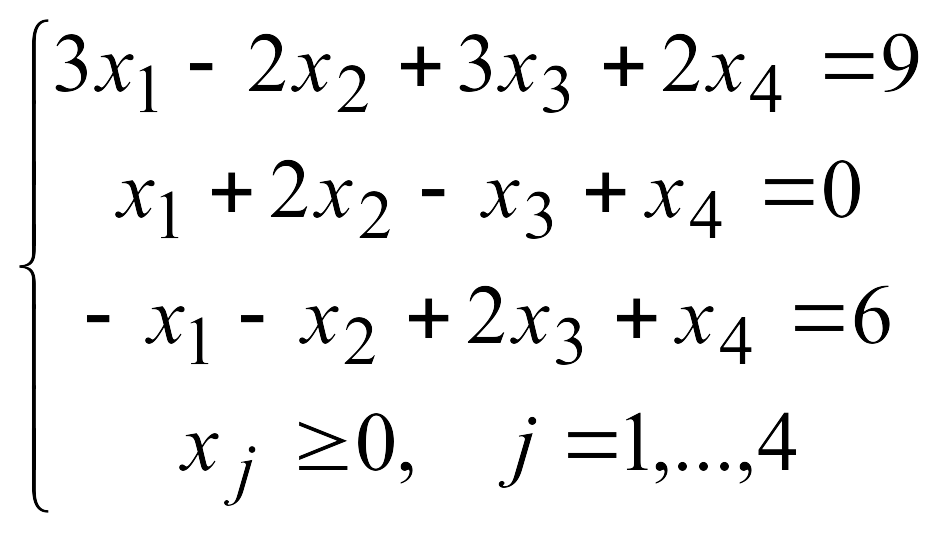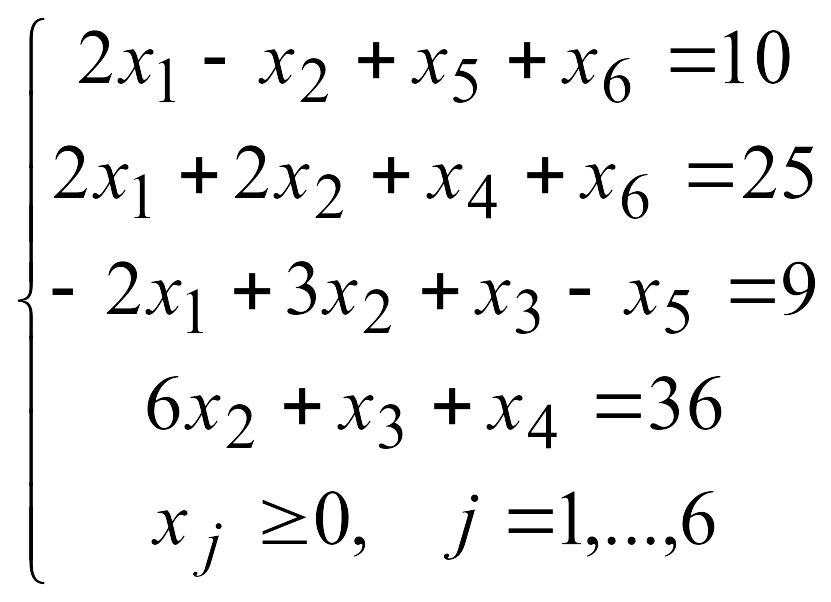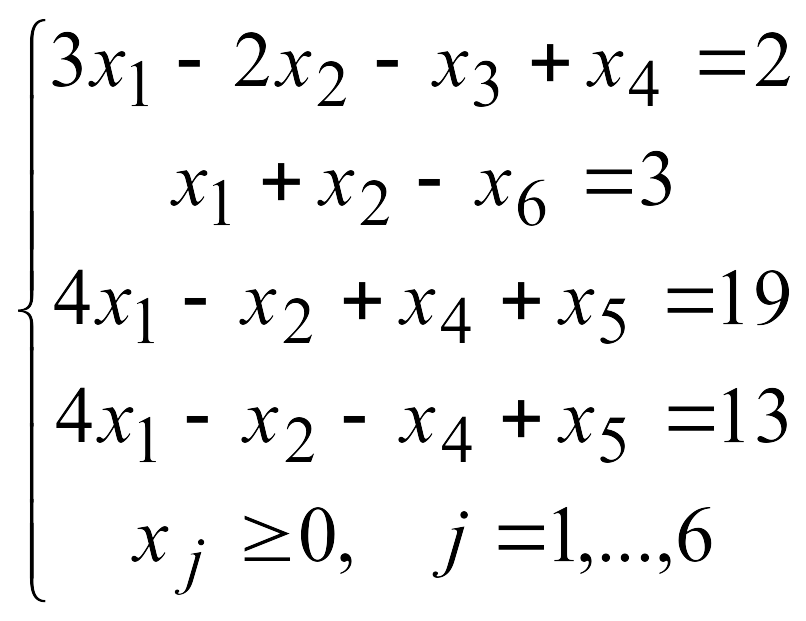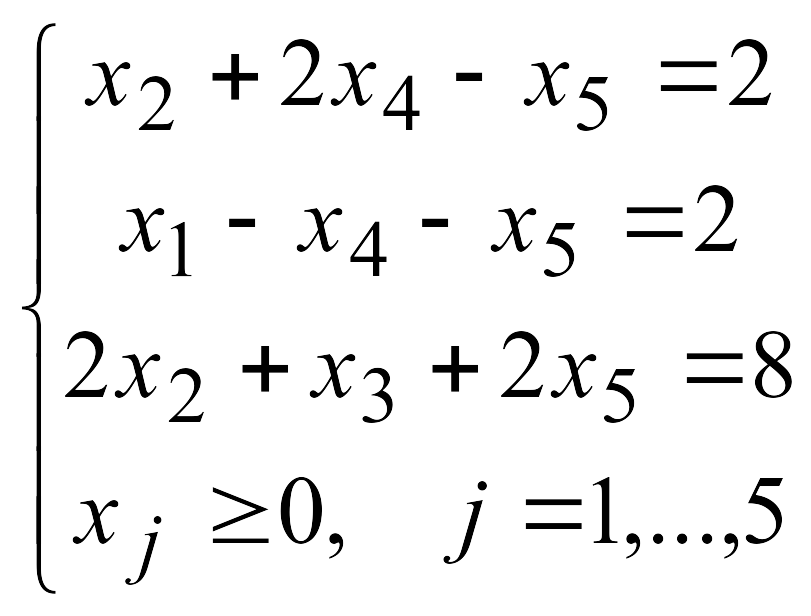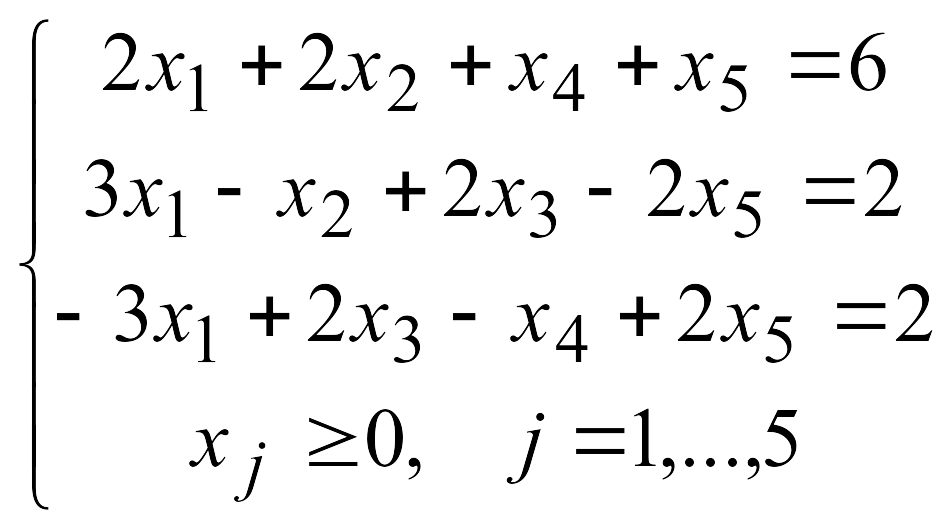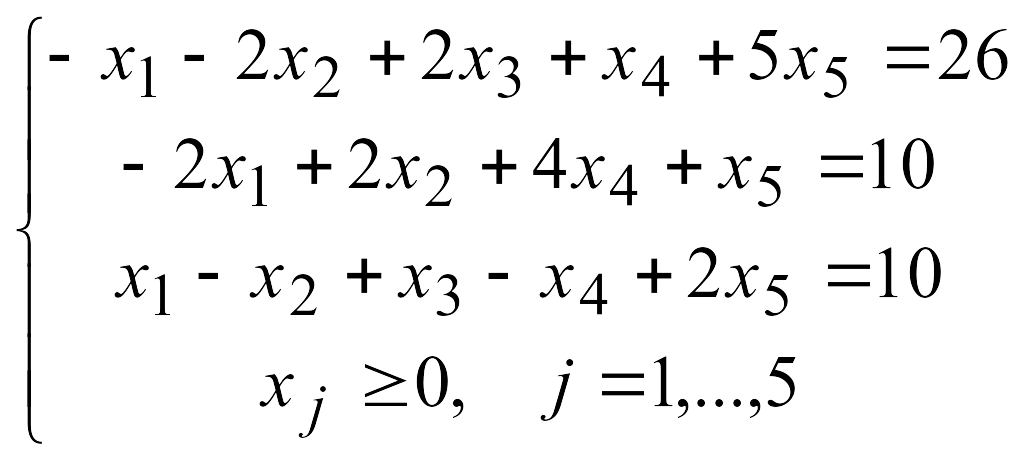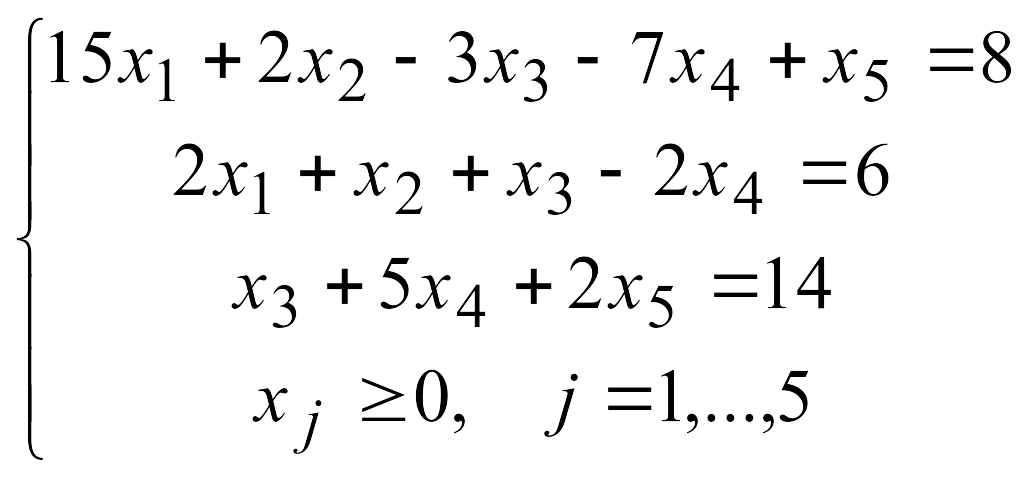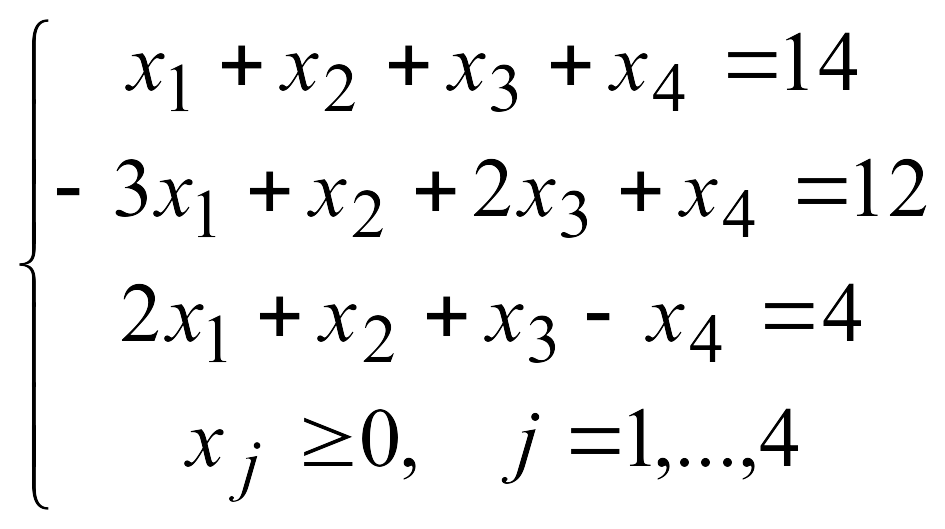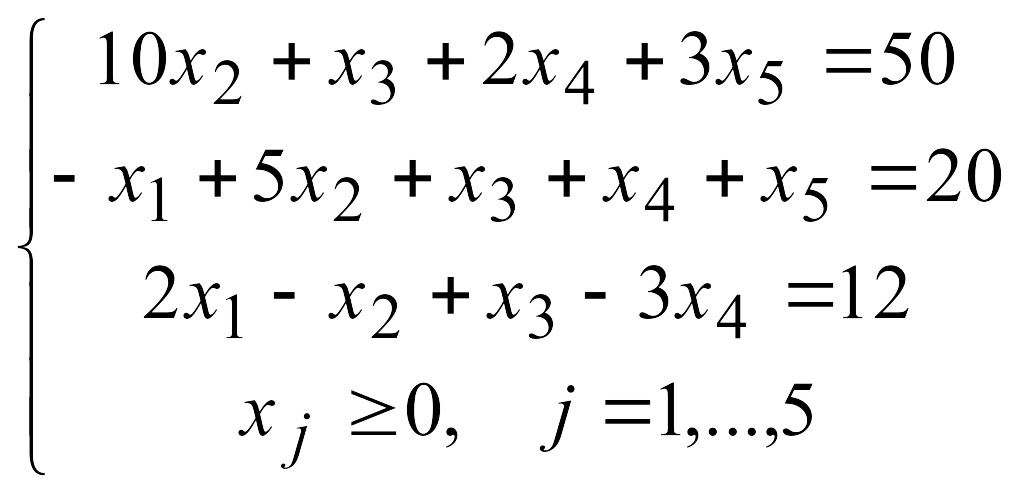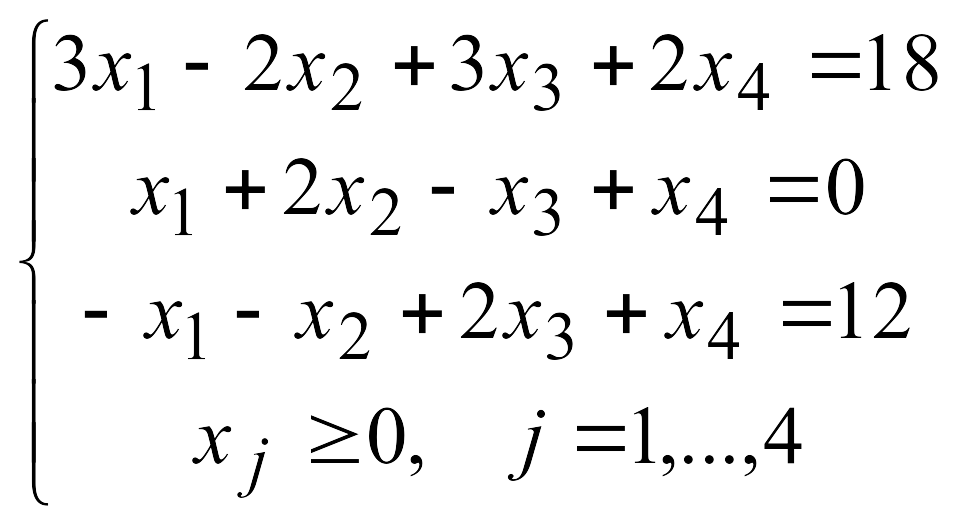Файл: МУ и задания Линейное программирование.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Методичка

Дисциплина: Методы оптимальных решений

Добавлен: 15.11.2018

Просмотров: 1937

Скачиваний: 35

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению индивидуального домашнего задания (контрольной работы)

Волгодонск

Рекомендуемая литература:

Задача 1

Задача 2

Образец выполнения задачи 5.



10.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

2

1

2

2100

В2

2

2

1

1200

Прибыль на единицу продукции

3

3

2



11.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

1

2

2

2200

В2

3

4

2

3000

Прибыль на единицу продукции

2

1

3



12.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

2

3

4

600

В2

3

1

2

800

Прибыль на единицу продукции

2

1

3



13.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

1

2

1

2000

В2

3

5

2

3000

Прибыль на единицу продукции

2

1

3



14.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

2

1

4

800

В2

2

1

3

900

Прибыль на единицу продукции

2

1

3




15.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

4

1

3

3000

В2

4

2

1

4000

Прибыль на единицу продукции

2

1

3



16.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

2

1

1

400

В2

2

3

2

600

Прибыль на единицу продукции

3

3

3



17.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

3

1

2

1800

В2

1

2

3

2000

Прибыль на единицу продукции

3

3

2



18.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

3

1

1

900

В2

2

3

1

1200

Прибыль на единицу продукции

3

3

2



19.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

2

2

1

2600

В2

3

2

2

1800

Прибыль на единицу продукции

3

3

2




20.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

2

1

2

1050

В2

2

2

1

600

Прибыль на единицу продукции

3

3

2



21.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

1

2

2

550

В2

3

4

2

750

Прибыль на единицу продукции

2

1

3



22.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

2

3

4

2400

В2

3

1

2

3200

Прибыль на единицу продукции

2

1

3



23.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

1

2

1

500

В2

3

5

2

750

Прибыль на единицу продукции

2

1

3



24.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

2

1

4

3200

В2

2

1

3

3600

Прибыль на единицу продукции

2

1

3



25.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

4

1

3

750

В2

4

2

1

1000

Прибыль на единицу продукции

2

1

3



26.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

2

1

1

1600

В2

2

3

2

2400

Прибыль на единицу продукции

3

3

3



27.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

3

1

2

2700

В2

1

2

3

300

Прибыль на единицу продукции

3

3

2



28.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

3

1

1

3600

В2

2

3

1

4800

Прибыль на единицу продукции

3

3

2



29.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

2

2

1

650

В2

3

2

2

450

Прибыль на единицу продукции

3

3

2



30.

Вид сырья

Расход сырья на единицу продукции

Общий запас сырья

А1

А2

А3

В1

2

1

2

4200

В2

2

2

1

2400

Прибыль на единицу продукции

3

3

2



Образец выполнения задачи 2.


1) Пусть исходные данные для решения задачи представлены в следующей таблице:

Вид сырья

Расход сырья на единицу продукции, ед.

Общий запас сырья, ед.

А1

А2

А3

В1

5

2

3

3200

В2

2

4

1

2800

Прибыль на единицу продукции, ден.ед.

2

5

3



Составим математическую модель задачи. Обозначим xi – количество продукции Ai .

Целевая функция – суммарная прибыль предприятия:

Общий расход ресурсов не должен превышать имеющегося запаса:

Все переменные xi неотрицательны:

Вводя дополнительные переменные, приведём задачу к каноническому виду:



Выберем в качестве базисных переменных x4 и x5. Полагая свободные переменные x1 = x2 = x3 = 0, имеем: x4 = 3200, x5 = 2800.

Таким образом, начальное допустимое решение имеет вид(

Составим симплекс-таблицу:

x1

x2

x3

bi

оценочное отношение

x4

5

2

3

3200

3200 : 2 = 1600

x5

2

4

1

2800

2800 : 4 = 700

F

2

5

3

0


a)







Выбираем в качестве разрешающего столбца столбец с наибольшим коэффициентом целевой функции. В качестве разрешающей строки берется строка, в которой достигается наименьшее оценочное отношение свободных членов к положительным элементам разрешающего столбца.

Пересчитываем симплекс-таблицу.

б)

x1

x5

x3

bi

оценочное отношение

x4

4

-1/2

5/2

1800

1800 : (5/2) = 720

x2

1/2

1/4

1/4

700

700 : (1/4) = 2800

F

-1/2

-5/4

7/4

-3500







Допустимое решение:

Новое решение не является оптимальным, т.к. в целевой функции есть свободная переменная с положительным коэффициентом. Переводим эту переменную в свободные (разрешающий столбец). Определяем разрешающую стоку и снова пересчитываем симплекс-таблицу.

в)

x1

x5

x4

bi

x3

8/5

-1/5

2/5

720

x2

8/5

3/10

-1/10

520

F

-33/10

-9/10

-7/10

-4760






Поскольку в строке целевой функции не осталось положительных коэффициентов, то найденное решение оптимально:

Следовательно, предприятию необходимо производить 520 ед. продукции А2 и 720 ед. продукции А3, при этом прибыль составит 4760 руб. Так как в оптимальном решении x4 = x5 = 0, то запасы обоих ресурсов будут исчерпаны полностью.







2) Составим двойственную ЗЛП. Обозначив двойственные цены на ресурсы через y1 и y2 и учитывая свойства двойственных задач, получаем:

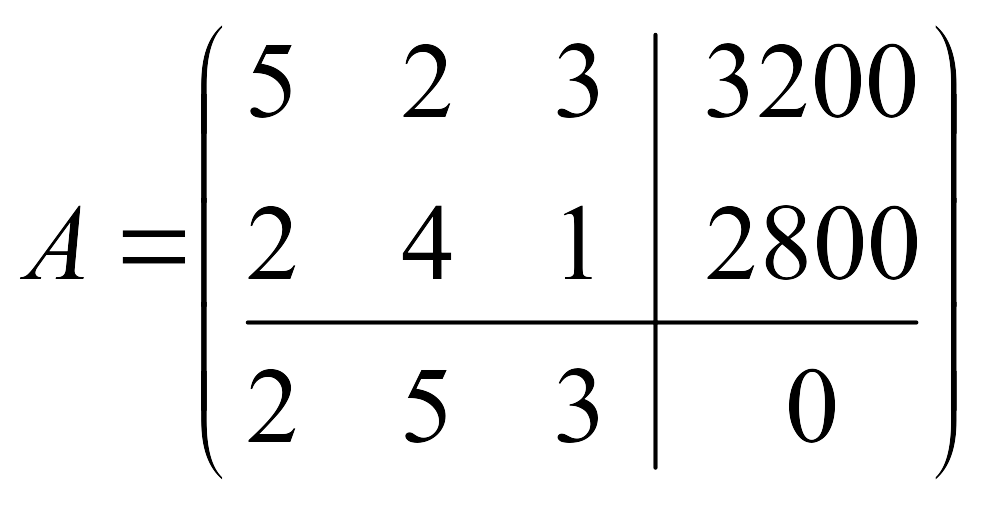
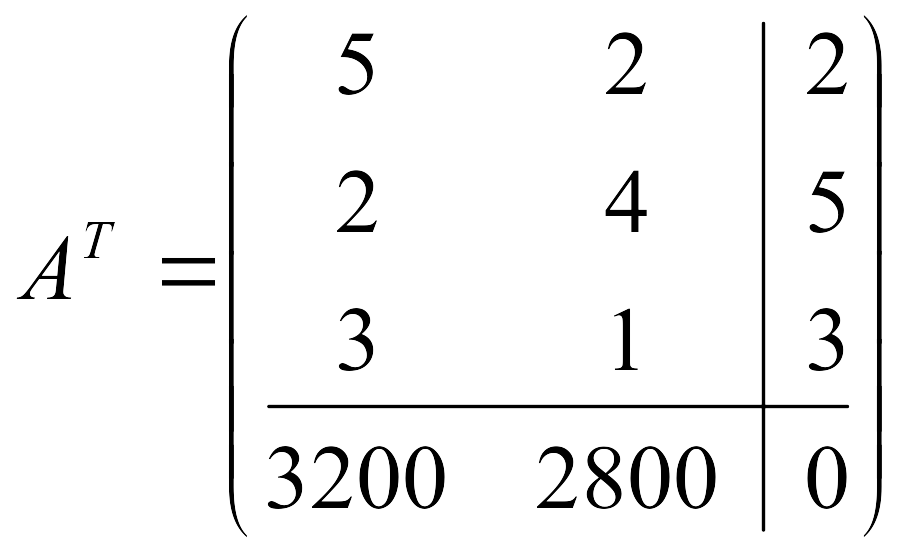
Приведём к каноническому виду:

,

Поскольку переменные y3, y4, y5 входят в ограничения со знаком «минус» то их нельзя выбирать в качестве базисных (полученное решение будет недопустимым).

Найдём начальное допустимое решение методом искусственного базиса. Введём в каждое ограничение искусственные переменные и составим вспомогательную ЗЛП:

а)

y1

y2

y3

y4

y5


оценочное отношение

t1

5

2

-1

0

0

2

2/5

t2

2

4

0

-1

0

5

5/2

t3

3

1

0

0

-1

3

1

-10

-7

1

1

1

-10



б)

t1

y2

y3

y4

y5


оценочное отношение

y1

1/5

2/5

-1/5

0

0

2/5

-

t2

-2/5

16/5

2/5

-1

0

21/5

21/5 : 2/5 = 21/2

t3

-3/5

-1/5

3/5

0

-1

2/5

2/5 : 3/5 = 2/3

2

-3

-1

1

1

-6


Поскольку искусственная переменная t1 перешла в свободные, соответствующий столбец можно исключить из симплекс-таблицы.

в)

y2

t3

y4

y5


оценочное отношение

y1

1/3

1/3

0

-1/3

1

1 : 1/3 = 3

t2

10/3

-2/3

-1

2/3

3

3 : 10/3 = 9/10

y3

-1/3

5/3

0

-5/3

3

-

-10/3

5/3

1

-2/3

-3


d)

t2

y4

y5


y1

-1/10

1/10

-2/5

7/10

y2

3/10

-3/10

1/5

9/10

y3

1/10

-1/10

-8/5

33/10

1

0

0

0


Получили допустимое решение

Выразим базисные переменные через свободные и подставим в целевую функцию:


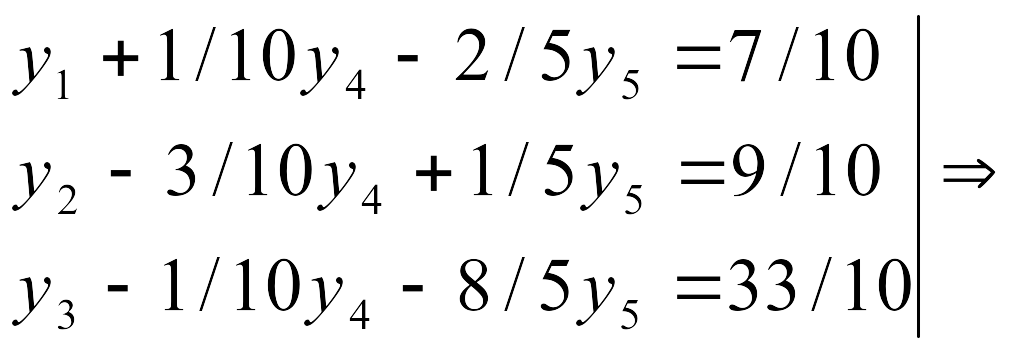
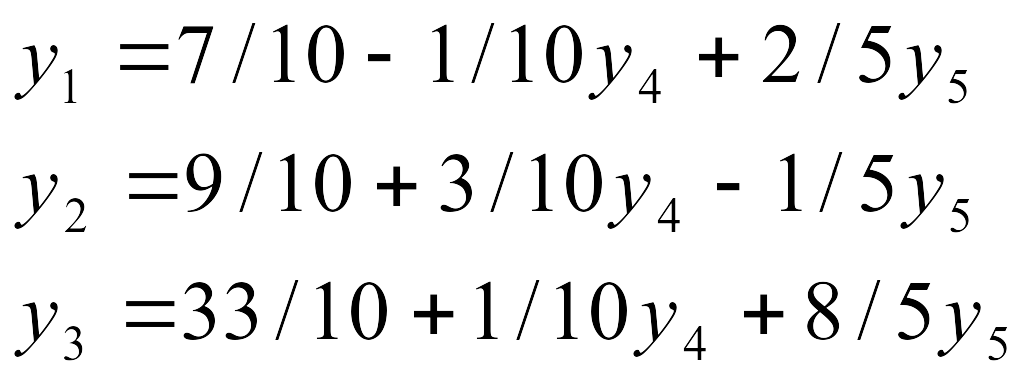
В целевой функции не осталось положительных коэффициентов, следовательно, найденное решение оптимально:


Покажем взаимосвязь двойственных задач.

1) Оптимальные значения целевых функций равны:

2) Установим взаимосвязь между основными и дополнительными переменными двойственных задач:

x1 x2 x3 x4 x5

y3 y4 y5 y1 y2

Значения базисных переменных одной из задач равны по модулю коэффициентам целевой функции другой задачи, выраженным через свободные переменные. Составим таблицу:


Переменные прямой задачи

x1

x2

x3

x4

x5

Компоненты оптимального решения x*

0

520

720

0

0

Коэффициенты целевой функции F

-33/10

-

-

-7/10

-9/10

Компоненты оптимального решения y*

33/10

0

0

7/10

9/10

Коэффициенты целевой функции Z

-

520

720

-

-

Переменные двойственной задачи

y3

y4

y5

y1

y2


Вопросы для самопроверки:

  1. Какие задачи называются двойственными?

  2. Опишите алгоритм построения двойственной задачи

  3. Сформулируйте основные теоремы двойственности.

  4. В чем смысл условий дополняющей нежесткости?

  5. Как найти решение двойственной задачи по известному решению прямой задачи?

Задача 3


Решить задачу линейного программирования симплекс-методом, найдя начальное допустимое решение методом искусственного базиса.


1.

2.

3.

4.

5.

6.

7.

8.

9.

10.



11.

12.

13.

14.

15.

16.

17.

18.

19.

20.


21.

22.

23.

24.

25.

26.

27.

28.

29.

30.




Образец выполнения задачи 3.


Решить следующую ЗЛП

найдя начальное допустимое решение методом искусственного базиса.


Приведём ограничения задачи к каноническому виду:


Введём искусственные переменные и составим вспомогательную ЗЛП:

Базисные переменные , ,

Составим вспомогательную целевую функцию:


Составим симплекс-таблицу:

Оценочное отношение

1

2

-3

1

-1

11

0

1

1

-4

0

8

-

3

2

0

2

0

46

-4

-4

3

-3

1

-57



Так как вспомогательная ЗЛП всегда решается на минимум, в строке нулевой функции не должно быть отрицательных коэффициентов. Выбираем столбец в качестве разрешающего и находим оценочные отношения (ОО). Строка - разрешающая (минимальное оценочное отношение). Пересчитываем симплекс-таблицу:

1

2

-3

1

-1

11

0

1

1

-4

0

8

-3

-4

9

-1

3

13

4

4

-9

1

-3

-13

Переменная перешла в свободные, следовательно, можно вычеркнуть столбец . Продолжая решение, получаем:

Оценочное отношение

2

-3

1

-1

11

-

1

1

-4

0

8

-4

9

-1

3

13

4

-9

1

-3

-13





0

0

1

0

0

0


Так как в строке целевой функции получились нули, то допустимое решение найдено:



Проверим, будет ли это решение оптимальным.

Запишем систему ограничений, соответствующую последней симплекс-таблице:

Выразим базисные переменные , , через свободные и подставим их в целевую функцию исходной задачи:

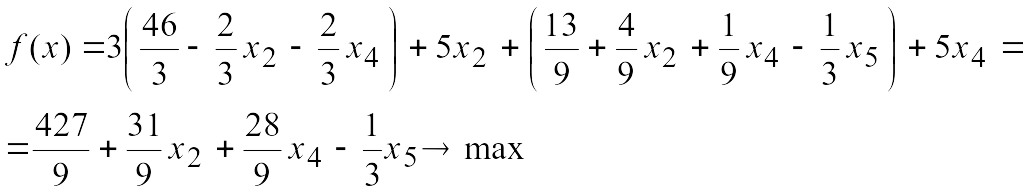
Так как в целевой функции, выраженной через свободные переменные, есть положительные коэффициенты, то допустимое решение не оптимально. Продолжим решение:

Смотрите также файлы