20.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		40	80	90	60
А1	120	4	5	6	7
А2	80	4	9	3	2
А3	50	6	5	2	3

21.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		60	40	90	60
А1	80	4	5	6	7
А2	120	4	9	3	2
А3	70	6	5	2	3

22.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		40	90	70	60
А1	80	4	5	6	7
А2	110	4	9	3	2
А3	50	6	5	2	3

23.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		90	60	60	40
А1	90	4	5	6	7
А2	120	4	9	3	2
А3	50	6	5	2	3

24.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		60	40	90	50
А1	80	4	5	6	7
А2	120	4	9	3	2
А3	50	6	5	2	3

25.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		40	50	90	60
А1	80	4	5	6	7
А2	120	4	9	3	2
А3	60	6	5	2	3

26.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		60	40	80	60
А1	50	4	5	6	7
А2	80	4	9	3	2
А3	110	6	5	2	3

27.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		40	90	100	60
А1	50	4	5	6	7
А2	80	4	9	3	2
А3	120	6	5	2	3

28.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		90	60	90	40
А1	50	4	5	6	7
А2	80	4	9	3	2
А3	120	6	5	2	3

29.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		60	40	90	70
А1	50	4	5	6	7
А2	70	4	9	3	2
А3	120	6	5	2	3

30.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		40	60	90	80
А1	50	4	5	6	7
А2	80	4	9	3	2
А3	120	6	5	2	3

---

Образец выполнения задачи 5.

Пусть матрица тарифов задана следующей таблицей:

		В1	В2	В3	В4
		200	150	100	150
А1	100	2	3	1	4
А2	300	3	1	2	2
А3	150	4	1	3	5

Проверим равенство запасов и потребностей:

; .

Равенство не выполняется ( ), следовательно, транспортная задача является открытой. Сведём её к закрытой модели путем введения фиктивного поставщика. Положим его запас равным дефициту ресурса (600 – 550 = 50), а тарифы на перевозки - равными 0.

Построим новую транспортную таблицу и определим начальное распределение методом северо-западного угла:

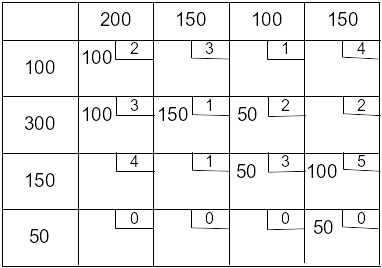
При этом стоимость перевозок составит:

(усл.ед).

Проверяем количество заполненных клеток – 7.

Определим потенциалы и оценки свободных клеток:

Так как число уравнений меньше числа неизвестных, выберем один из потенциалов произвольно. Положив , получим:

Найдём оценки свободных клеток :

Поскольку среди оценок свободных клеток есть отрицательные ( ; ), то найденный план оптимальным не является.

Для перераспределения поставок выбираем клетку с наибольшей по модулю отрицательной оценкой – клетка (2; 4) – и строим цикл, первая вершина которго находится в выбранной клетке, а остальные – в заполненных клетках. В вершинах цикла поочередно расставляем знаки «+» и «–», начиная со свободной клетки.

Определяем размер перераспределяемой поставки (минимальное из знач6ений в клетках со знаком «–»): min (50; 100) = 50. Перераспределяем 50 единиц ресурса и получаем новый план поставок:

Новая стоимость перевозок составит:

(усл.ед)

Определим потенциалы и оценки свободных клеток:

План не оптимален. Выберем клетку (3; 2) и строим цикл:

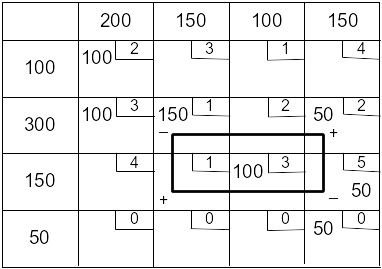
Размер перераспределяемой поставки: min (150; 50) = 50.

Новый план:

Стоимость поставок: усл.ед.

Потенциалы:

Оценки свободных клеток:

Строим цикл для клетки (1;3):

Размер перераспределяемой поставки: min (100;100;100) = 100.

Новый план:

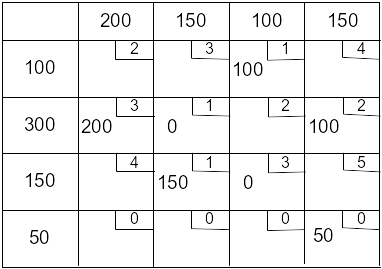
Стоимость перевозок: усл.ед..

Внимание! Вырожденное решение: если обнуляются несколько клеток, то только одна становится пустой, остальные считаются заполненными (нулями).

Потенциалы:

Оценки свободных клеток:

Строим цикл для клетки (2;3):

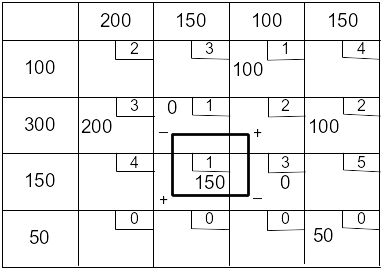
Внимание! Холостой ход – перераспределяется нулевая поставка
(min (0; 0) = 0), стоимость не меняется.

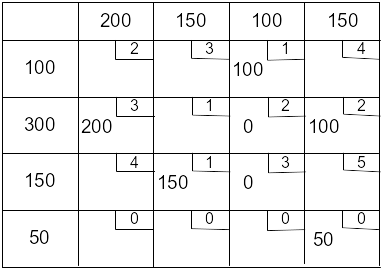
Стоимость перевозок также не меняется (усл.ед.), однако из-за изменения заполненных клеток пересчитываем потенциалы:

Оценки свободных клеток:

Строим цикл для клетки (4; 1):

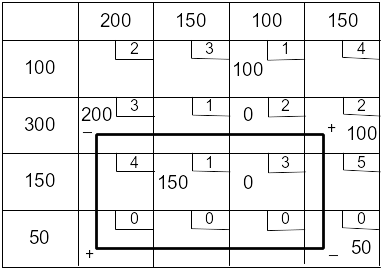
Перераспределяем min (50;200) = 50.

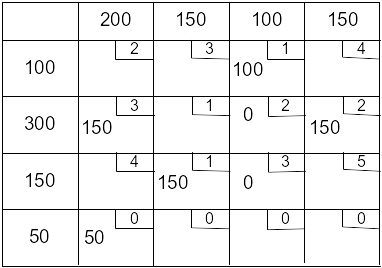
усл.ед..

Снова находим потенциалы:

Оценки свободных клеток:

Поскольку все оценки неотрицательны, найденный план является оптимальным. Однако оптимальное решение не единственно, поскольку среди оценок свободных клеток есть нулевые.

Составим распределение поставок методом наименьших затрат (минимального элемента). На каждом шаге заполняется клетка с минимальным тарифом из оставшихся. (Внизу указан порядок заполнения клеток.)

---

усл.ед.

Вопросы для самопроверки:

1. Какая транспортная задача называется открытой?

2. Как свести открытую задачу к закрытой?

3. Опишите порядок построения начального плана методом северо-западного угла и наименьших затрат?

4. Всегда ли план, полученный методом наименьших затрат, является оптимальным?

5. В чем смысл оценок свободных клеток?

6. Как определяется размер перераспределяемой поставки?

7. Как определить, будет ли оптимальное решение единственным?

8. Если оптимальное решение не единственно, как получить другие оптимальные решения?

9. В чем смысл фиктивных поставок?

---

Задача 6

Используя минимаксные стратегии, определить верхнюю и нижнюю цену игры, заданной платежной матрицей, цену игры и оптимальные чистые стратегии игроков.

1.	4	5	1		8.	4	-1	6		15.	5	0	7
	1	2	-2			3	-2	5			-3	-8	-1
	6	7	3			6	1	8			6	1	8
2.	5	3	1		9.	0	-1	6		16.	1	7	3
	2	0	-2			1	0	7			-2	4	0
	7	5	3			2	1	8			6	12	8
3.	5	3	4		10.	3	-1	6		17.	13	9	15
	4	2	3			6	2	9			-2	-6	0
	7	5	6			5	1	8			6	2	8
4.	1	3	4		11.	8	17	11		18.	5	6	7
	4	6	7			6	15	9			3	4	5
	3	5	6			5	14	8			6	7	8
5.	7	3	4		12.	8	4	11		19.	8	4	10
	0	-4	-3			-4	-8	-1			3	-1	5
	9	5	6			5	1	8			6	2	8
6.	5	-2	7		13.	-1	-7	2		20.	4	-2	5
	4	-3	6			3	-3	6			7	1	8
	6	-1	8			5	-1	8			5	-1	6
7.	-1	-7	-4		14.	3	7	0		21.	8	-2	5
	6	0	3			6	10	3			11	1	8
	5	-1	2			5	9	2			10	0	7
22.	5	-2	3		25.	-7	-1	-2		28.	0	4	3
	1	-6	-1			0	6	5			1	5	4
	6	-1	4			-1	5	4			-1	3	2
23.	7	1	8		26.	0	5	3		29.	8	1	9
	0	-6	1			1	6	4			2	-5	3
	3	-3	4			4	9	7			7	0	8
24.	0	5	3		27.	6	5	7		30.	5	1	9
	5	10	8			2	1	3			-2	-6	2
	1	6	4			7	6	8			4	0	8

---

Образец выполнения задачи 6.

Игра задана платёжной матрицей:

.

Определим верхнюю и нижнюю цену игры. Поскольку первый игрок придерживается максиминной стратегии, для каждой из стратегий первого игрока определяется наихудший вариант (наименьший выигрыш), а затем из них выбирается наилучший (наибольший).

Нижняя цена игры:

Второй игрок следует минимаксной стратегии: для каждой стратегии второго игрока выбирается наихудший вариант (наибольший проигрыш), а затем из них выбирается наилучший (наименьший).

Верхняя цена игры: .

Для заданной платежной матрицы находим:

	4	9	5	3	3
	7	8	6	9	6
	7	4	2	6	2
	8	3	4	7	3
	8	9	6	9

Поскольку , то игра имеет седловую точку, и существует оптимальное решение игры в чистых стратегиях.

Оптимальная стратегия первого игрока - , оптимальная стратегия второго игрока - . Цена игры .

Вопросы для самопроверки:

1. Что такое матричная игра с нулевой суммой?

2. В чем смысл элементов платёжной матрицы?

3. Что такое чистая стратегия?

4. Что называется ценой игры?

5. Что такое седловая точка?

6. В чем сущность оптимальных чистых стратегий?

Задача 7

Определить верхнюю и нижнюю цену игры, заданной платежной матрицей. Упростить игру, если это возможно. Найти решение в смешанных стратегиях графически и с помощью симплекс-метода.

1.	4	16	-8	1		11.	3	8	0	2		21.	4	3	0	-2
	-5	12	20	8			-4	-2	20	12			3	1	8	2
2.	5	-1	-11	-6		12.	-1	14	-1	-6		22.	1	11	-2	-4
	-4	6	5	2			11	10	-5	-2			3	10	-8	12
3.	10	-2	10	18		13.	4	6	12	8		23.	4	-6	2	8
	4	21	22	8			7	10	4	13			1	4	5	3
4.	10	6	-18	18		14.	0	12	-2	-8		24.	10	14	-8	8
	4	2	10	8			2	-8	-4	-2			-7	10	-4	13
5.	7	3	5	-11		15.	11	-4	-4	1		25.	2	9	3	7
	3	2	2	5			3	-2	4	-5			8	7	9	6
6.	11	-4	8	17		16.	2	3	-2	7		26.	1	7	2	9
	3	6	2	5			8	-3	1	6			9	11	7	3
7.	15	-5	11	3		17.	2	3	3	7		27.	-1	9	3	7
	7	-3	5	-11			4	1	2	1			9	1	7	13
8.	-1	31	23	17		18.	5	-1	5	14		28.	-3	15	5	15
	12	7	11	14			-4	13	5	7			4	-7	15	9
9.	-3	15	15	-15		19.	10	7	4	9		29.	10	2	14	9
	-4	23	11	21			-4	23	6	2			5	9	3	3
10.	10	2	11	9		20.	3	4	7	2		30.	2	8	1	3
	5	7	3	7			5	1	3	9			5	2	3	3

---