Добавлен: 15.11.2018
Просмотров: 1933
Скачиваний: 35
Образец выполнения задачи 7.
Пусть матричная игра задана платежной матрицей:
|
|
В1 |
В2 |
В3 |
В4 |
|
А1 |
0 |
12 |
-1 |
-4 |
|
А2 |
1 |
10 |
-8 |
12 |
Определим нижнюю и верхнюю цену игры:
|
|
В1 |
В2 |
В3 |
В4 |
|
|
А1 |
0 |
12 |
-1 |
-4 |
-4 |
|
А2 |
1 |
10 |
-8 |
12 |
-8 |
|
|
1 |
12 |
-1 |
12 |
|
Так как нижняя и верхняя цена игры не совпадают, то не существует оптимального решения в чистых стратегиях.
Упростим игру, вычеркнув доминируемые (обеспечивающие заведомо больший проигрыш) стратегии для второго игрока:
|
|
В1 |
В2 |
В3 |
В4 |
→ |
|
В1 |
В3 |
В4 |
→ |
|
В3 |
В4 |
|
А1 |
0 |
12 |
-1 |
-4 |
А1 |
0 |
-1 |
-4 |
А1 |
-1 |
-4 |
||
|
А2 |
1 |
10 |
-8 |
12 |
А2 |
1 |
-8 |
12 |
А2 |
-8 |
12 |
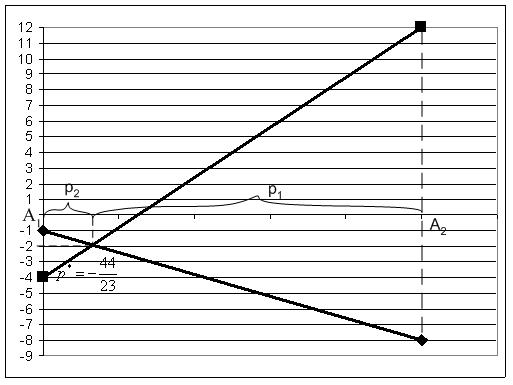
Решим задачу графически.
Для первого игрока
обозначим р1 – вероятность выбора
стратегии А1,
р2 –
вероятность выбора стратегии А2.
Построим линии выигрыша для случаев,
если второй игрок выбирает стратегии
В3 иВ4 соответственно.
Оптимальное решение – верхняя точка
нижней огибающей этих прямых.
|
|
υ= –p1 – 8(1 – p1) υ= –4p1 + 12(1 – p1) p1 – 8(1–p1) = –4p1 + 12(1–p1) 7p1 – 8 = – 16 p1 + 12 23 p1 = 20 p1
=
p2
= 1 –
υ*
=
|
Аналогично поступаем для второго игрока, только на этот раз выбираем нижнюю точку на верхней огибающей.
|
|
–q1 – 4(1–q1) = –8q1 + 12(1– q1) 3q1 – 4 = – 20 q1 + 12 23q1 =16 q1
= q2
= 1 –
υ*
=
|
Решим задачу симплекс-методом. Для этого преобразуем элементы платежной матрицы, чтобы не было отрицательных элементов.
|
|
В3 |
В4 |
+8 → |
|
В3 |
В4 |
|
А1 |
-1 |
-4 |
А1 |
7 |
4 |
|
|
А2 |
-8 |
12 |
А2 |
0 |
20 |
Запишем условия оптимальности смешанных стратегий.
Для первого
игрока: ![]()
Для второго
игрока: ![]()
Разделим каждое
из неравенств на υ
и введем
замену:
![]() .
.
Сформулируем пару двойственных задач.
|
Для первого игрока:
|
Для второго игрока:
|
Решим вторую задачу симплекс-методом, приведя ее к каноническому виду:
![]()
![]()
|
|
y1 |
y2 |
|
|
→ |
|
y1 |
y4 |
|
|
|
y3 |
y4 |
|
|
y3 |
7 |
4 |
1 |
|
|
y3 |
7 |
|
|
|
y1 |
|
|
|
|
y4 |
0 |
20 |
1 |
|
|
y2 |
0 |
|
|
→ |
y2 |
0 |
|
|
|
z |
1 |
1 |
0 |
|
|
z |
1 |
|
|
|
z |
|
|
|
Оптимальное
решение: y1*=![]() ,
y2*=
,
y2*=![]() ,
z*
=
,
z*
=![]() .
.
На основе принципа двойственности найдем оптимальное решение первой задачи. Для этого составим следующую таблицу:
|
Прямая |
|
x1 |
x2 |
x3 |
x4 |
|
x* |
|
|
0 |
0 |
|
|
f* |
|
|
|
|
|
|
Двойственная |
|
y3 |
y4 |
y1 |
y2 |
|
y* |
0 |
0 |
|
|
|
|
z* |
|
|
|
|
Оптимальное решение
первой задачи: x1*=![]() ,
x2*=
,
x2*=![]() ,
f*=
,
f*=![]() .
.
Найдем цену игры с преобразованной платежной матрицей и оптимальные стратегии игроков.
υ′
= 1/ f
* =
![]() .
.
p1
=
![]() =
=
![]() , p2
=
, p2
=
![]() =
=
![]() .
.
q1
=
![]() =
=
![]() , q2
=
, q2
=
![]() =
=
![]() .
.
Оптимальные
стратегии:
![]()
Цена
исходной игры:
υ
=
![]() –
8 =
–
8 =
![]()
Вопросы для самопроверки:
-
В каком случае не существует оптимального решения в чистых стратегиях?
-
Что называется смешанной стратегией?
-
Как в случае смешанных стратегий определяется цена игры?
-
Что такое доминирующие и доминируемые стратегии?
-
Сформулируйте условия оптимальности смешанных стратегий.
-
Почему элементы платежной матрицы при решении симплекс-методом должны быть неотрицательными?
-
как в матричных играх используется принцип двойственности?
-
В каком случае матричную игру можно решить графически?