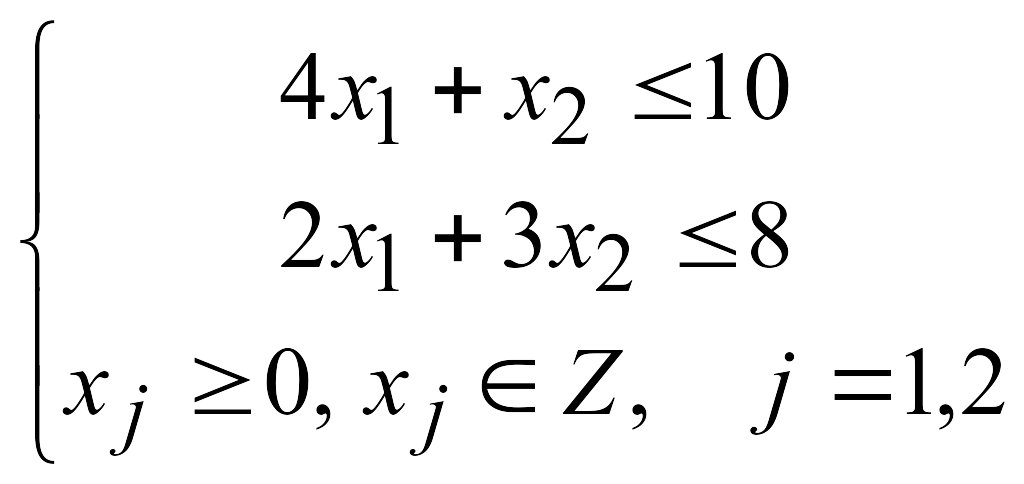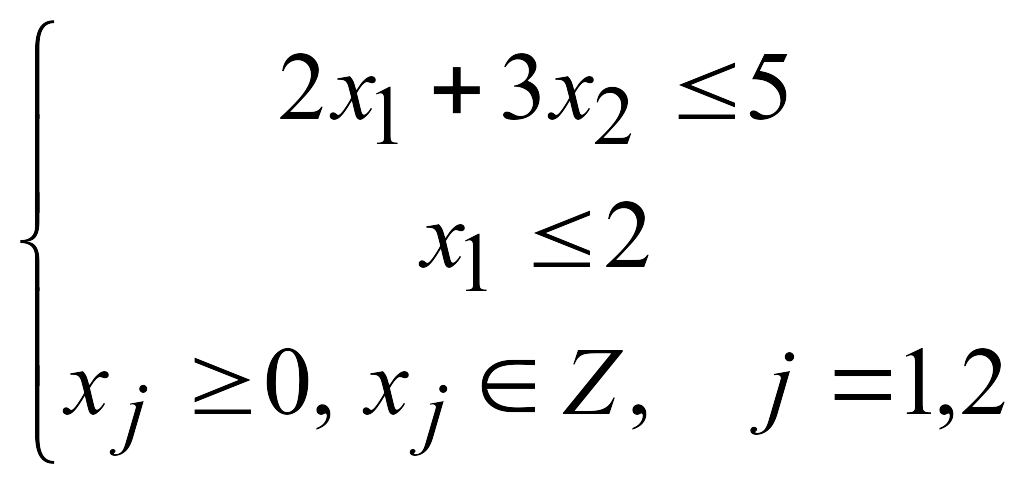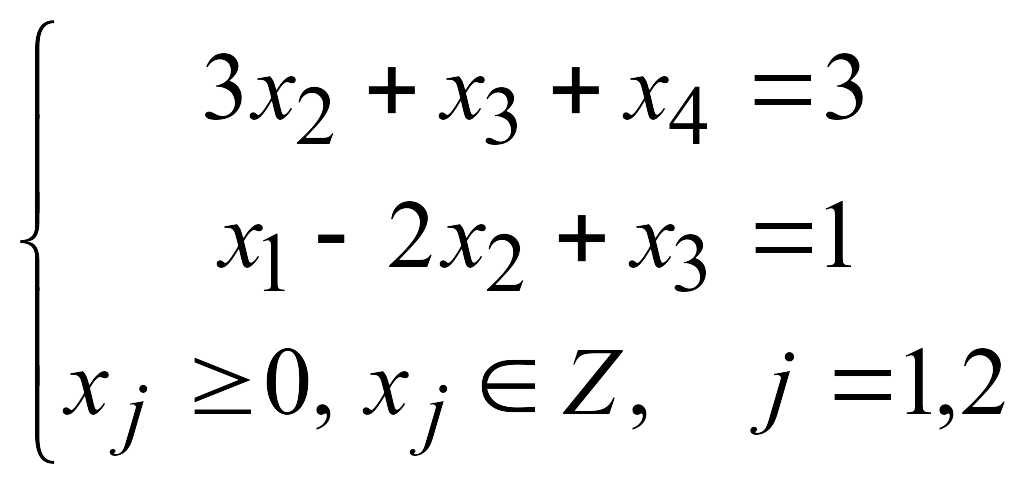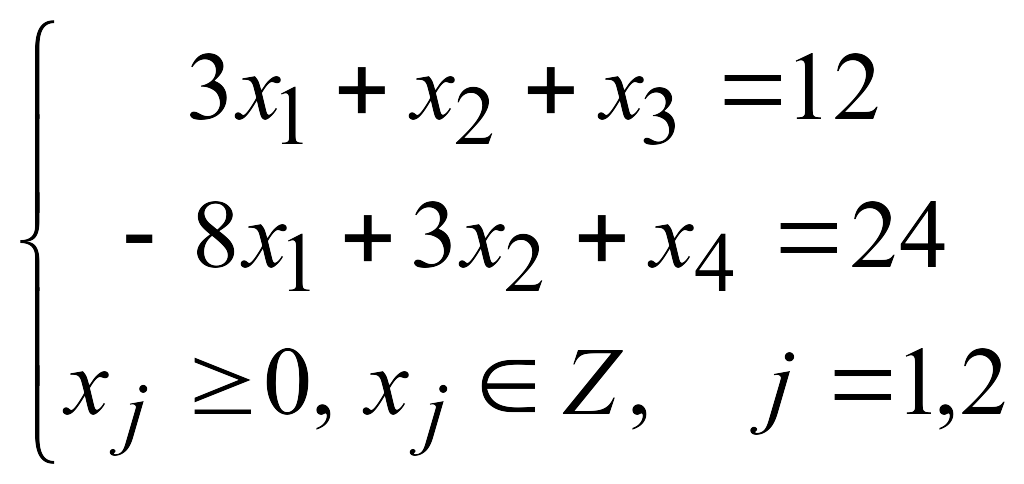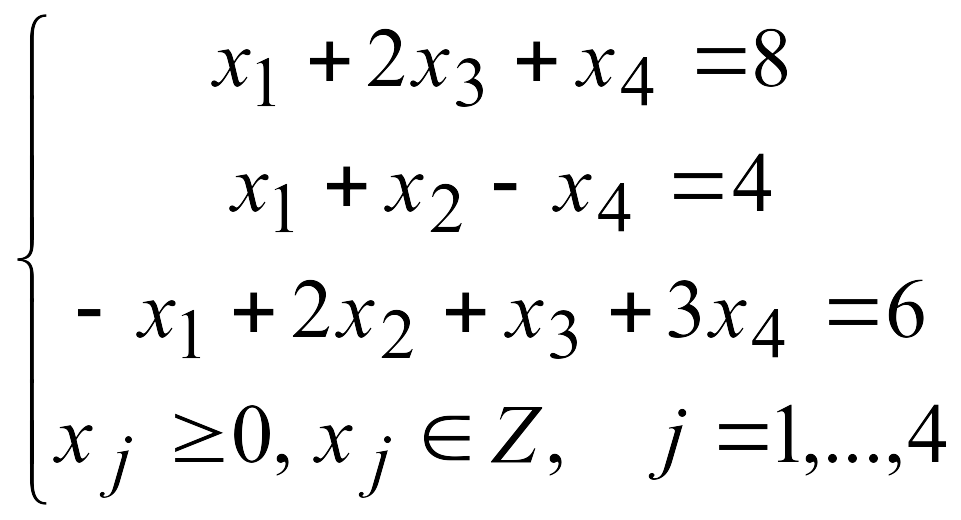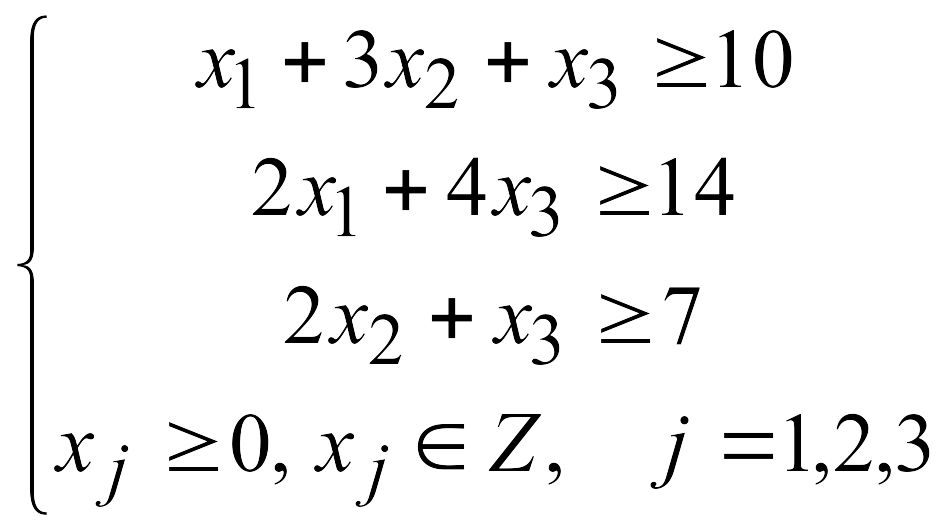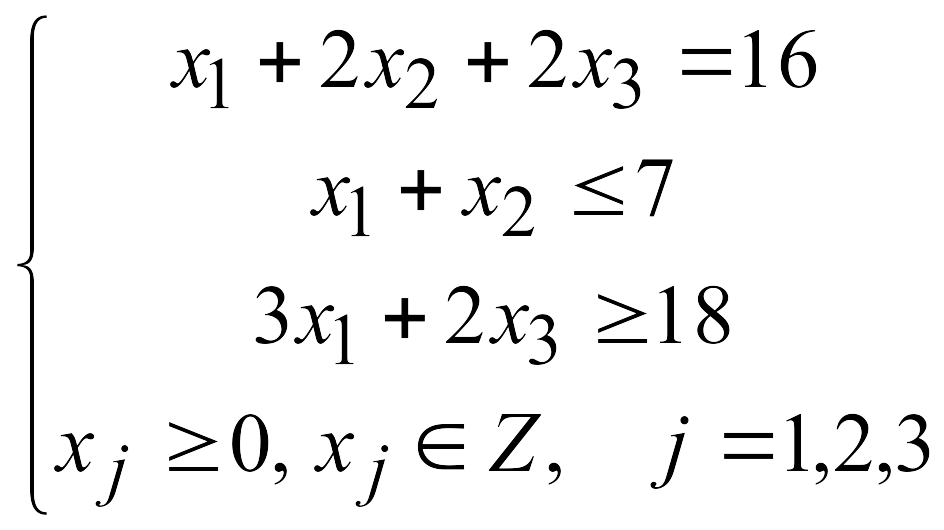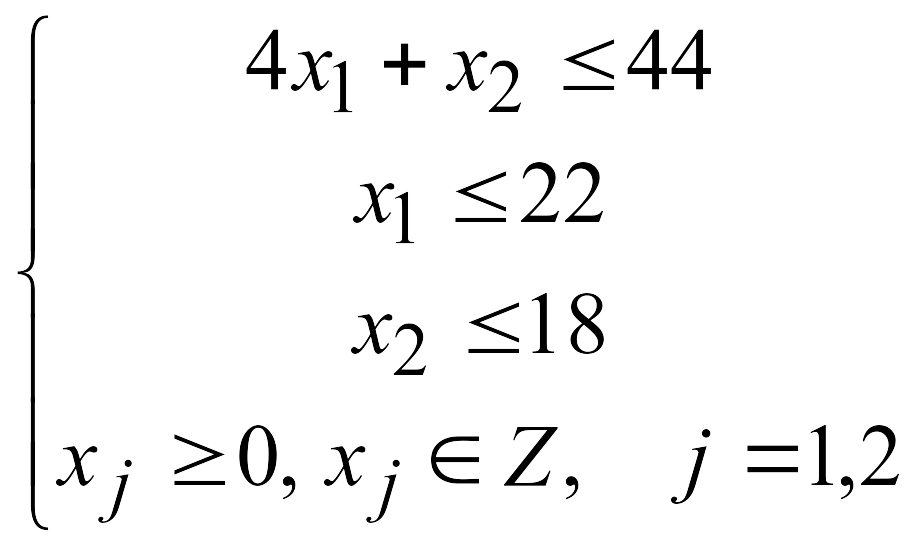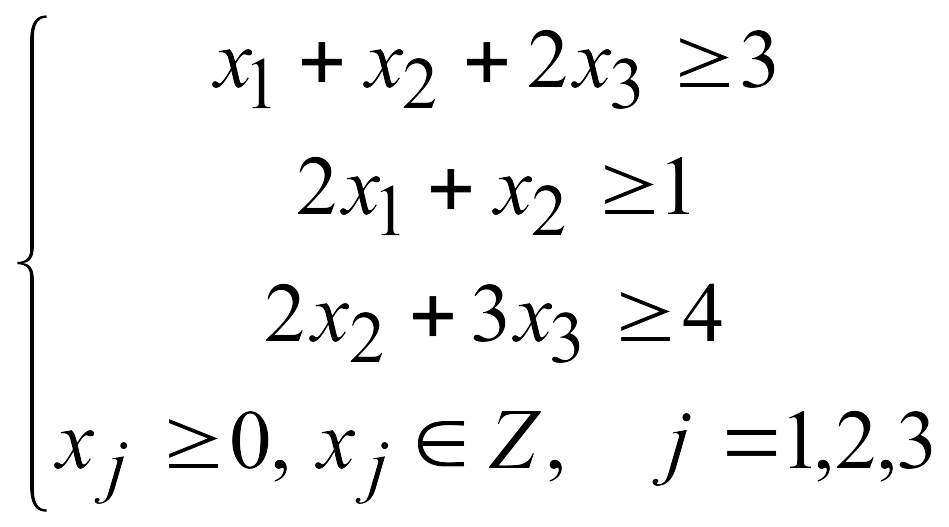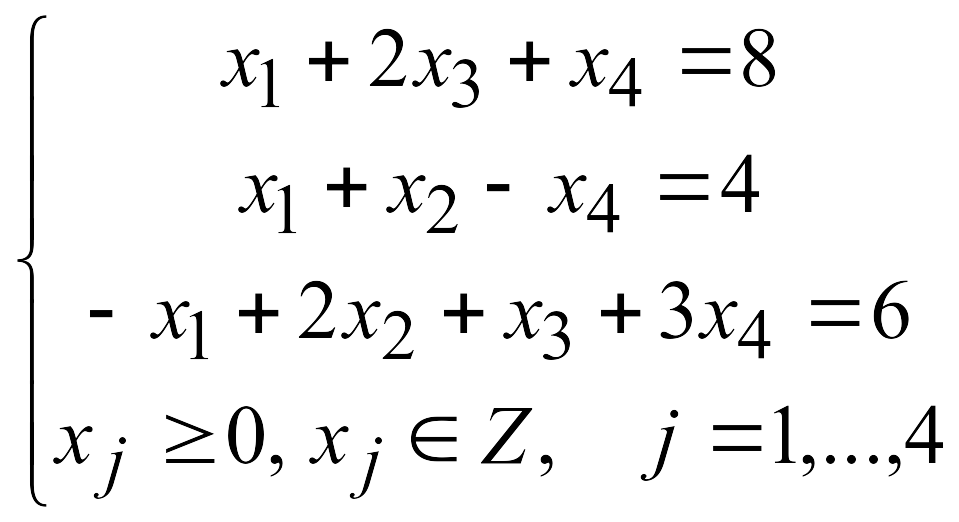Файл: МУ и задания Линейное программирование.doc

					ОО
			0
					-
					-

					ОО
	1		0	23
				96
				4	-
				-119

				5
				18
				10
				-125

Поскольку в строке целевой функции не осталось положительных коэффициентов, то оптимальное (максимальное) решение найдено:

,

.

Примечание: Обратите внимание, что в ответе указываются только значения исходных переменных.

Вопросы для самопроверки:

1. В каком случае в ограничения задачи вводятся искусственные переменные?

2. В каком случае можно вычеркнуть искусственную переменную?

3. Как определить, будет ли найденное допустимое решение оптимальным?

4. Что можно сказать об исходной задаче, если оптимум вспомогательной задачи отличен от 0?

5. Что следует делать, если в оптимальном решении вспомогательной ЗЛП искусственная переменная является базисной?

6. Почему вспомогательная ЗЛП всегда имеет решение?

---

Задача 4

Решить полностью целочисленную задачу линейного программирования методом Гомори. Если это возможно, найти решение задачи геометрически.

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.

11.	12.
13.	14.
15.	16.
17.	18.
19.	20.

21.	22.
23.	24.
25.	26.
27.	28.
29.	30.

Образец выполнения задачи 4.

Решить методом Гомори полностью целочисленную ЗЛП:

1. Решаем задачу с отброшенным условием целочисленности, для чего приведём ограничения к каноническому виду:

Выберем переменные , в качестве базисных и решим ЗЛП с помощью симплекс-таблиц:

ОО 2 1 5 2 3 9 1 1 0

ОО 2 3 -3

2

Оптимальное решение найдено:

Однако переменная не удовлетворяет условию целочисленности

2. Построим правильное отсечение, введя дополнительное ограничение. Для этого определим дробные части коэффициентов в строке :

.

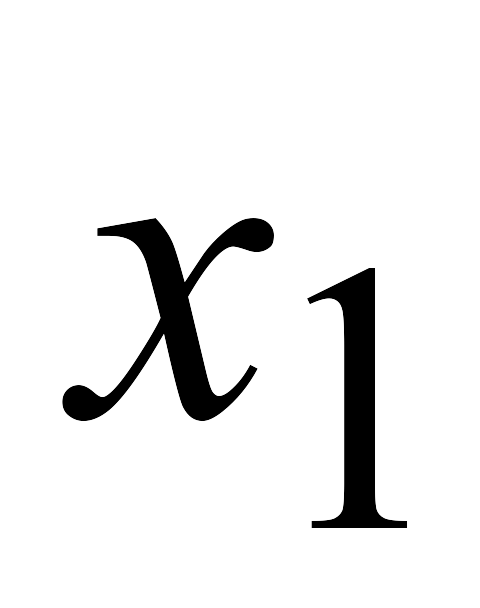Добавляем переменную , для которой коэффициенты в симплекс-таблице равны дробным частям строки , взятым с обратным знаком, и продолжаем решение симплекс-методом.

Строка с отрицательной правой частью является разрешающейся. В качестве разрешающегося столбца выбирается столбец, в котором модуль отношения коэффициентов целевой функции к отрицательным элементам разрешающей строки будет минимальным. (В нашем случае можно выбирать любой столбец)

2	1 -1 1 1 1 0

Найдено оптимальное решение ЗЛП с дополнительным ограничением:

---

.

Однако оно снова не является целочисленным.

3) Формируем отсечение по строке , добавляя переменную .

1 -1 1 1 1 0 0

3 -1 0 -2 1 3 -4 1 2 -3 0 1 -1 0 -3

Найденное оптимальное решение удовлетворяет условию целочисленности:

, .

4) Поскольку исходная ЗЦП содержит только 2 переменных, её можно решить графически. Графическое решение ЗЦП практически не отличается от решения обычной ЗЛП, однако линия уровня перемещается лишь до тех пор, пока она проходит через точки с целочисленными координатами.

Графическое решение рассматриваемой ЗЦП приведено на рис.2. Прямые (1) и (2) соответствуют исходным ограничениям задачи.

Вектор-градиент имеет координаты

Прямая (3) – линия уровня, определяющая оптимальное решение нецелочисленной задачи.

Прямая (4) – линия уровня, определяющая оптимальное решение ЗЦП.

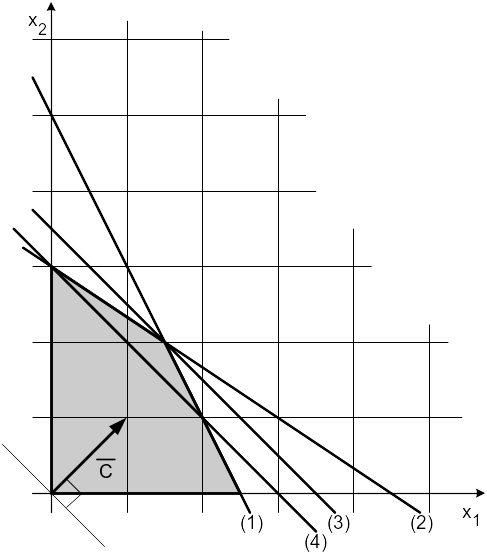
Рисунок 2 – Графическое решение задачи целочисленного программирования

Графическое решение показывает, что помимо найденного методом Гомори оптимального решения , существует ещё 2 точки с целыми координатами и , обеспечивающие то же значение целевой функции , и, следовательно, также являющиеся оптимальными решениями.

Неединственность оптимального решения можно заметить и по симплекс-таблице: в строке целевой функции есть нулевой коэффициент.

Вопросы для самопроверки:

1. Какова сущность задачи целочисленного программирования?

2. Почему при решении ЗЦП нельзя округлить найденное нецелочисленное решение?

3. В чём сущность методов отсечения для решения ЗЦП?

4. Какое отсечение называется правильным?

5. Что такое целая и дробная часть числа?

6. Перечислите основные этапы алгоритма Гомори для полностью целочисленной ЗЛП.

---

Задача 5

В транспортной задаче найти начальное распределение поставок методом северо-западного угла и методом наименьших затрат. Определить затраты при этих распределениях поставок.

Решить транспортную задачу методом потенциалов, взяв в качестве опорного плана решение, найденное методом северо-западного угла. Выяснить, будет ли найденное оптимальное решение единственным.

1.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		60	40	90	60
А1	120	4	4	7	5
А2	80	2	3	6	8
А3	60	5	1	5	9

2.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		40	90	60	70
А1	120	4	4	7	5
А2	80	2	3	6	8
А3	40	5	1	5	9

3.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		90	60	70	40
А1	120	4	4	7	5
А2	80	2	3	6	8
А3	50	5	1	5	9

4.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		60	40	90	60
А1	120	4	4	7	5
А2	90	2	3	6	8
А3	50	5	1	5	9

5.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		40	50	90	60
А1	120	4	4	7	5
А2	80	2	3	6	8
А3	50	5	1	5	9

6.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		60	40	90	80
А1	80	4	4	7	5
А2	110	2	3	6	8
А3	50	5	1	5	9

7.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		40	90	60	80
А1	80	4	4	7	5
А2	120	2	3	6	8
А3	60	5	1	5	9

8.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		90	60	60	40
А1	80	4	4	7	5
А2	110	2	3	6	8
А3	50	5	1	5	9

9.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		60	40	90	60
А1	90	4	4	7	5
А2	120	2	3	6	8
А3	50	5	1	5	9

---

10.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		70	60	90	60
А1	80	4	4	7	5
А2	120	2	3	6	8
А3	50	5	1	5	9

11.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		60	40	80	60
А1	50	4	4	7	5
А2	80	2	3	6	8
А3	120	5	1	5	9

12.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		40	100	60	60
А1	50	4	4	7	5
А2	80	2	3	6	8
А3	120	5	1	5	9

13.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		90	60	60	40
А1	50	4	4	7	5
А2	80	2	3	6	8
А3	100	5	1	5	9

14.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		60	40	90	60
А1	50	4	4	7	5
А2	60	2	3	6	8
А3	120	5	1	5	9

15.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		40	60	80	60
А1	60	4	4	7	5
А2	80	2	3	6	8
А3	120	5	1	5	9

16.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		60	40	90	60
А1	100	4	5	6	7
А2	80	4	9	3	2
А3	50	6	5	2	3

17.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		40	100	60	60
А1	120	4	5	6	7
А2	80	4	9	3	2
А3	50	6	5	2	3

18.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		90	60	60	40
А1	130	4	5	6	7
А2	80	4	9	3	2
А3	50	6	5	2	3

19.

Поставщики и их мощности		Потребители и их спрос
		В1	В2	В3	В4
		60	40	90	60
А1	120	4	5	6	7
А2	70	4	9	3	2
А3	50	6	5	2	3

---