Добавлен: 15.11.2018
Просмотров: 2046
Скачиваний: 8
6
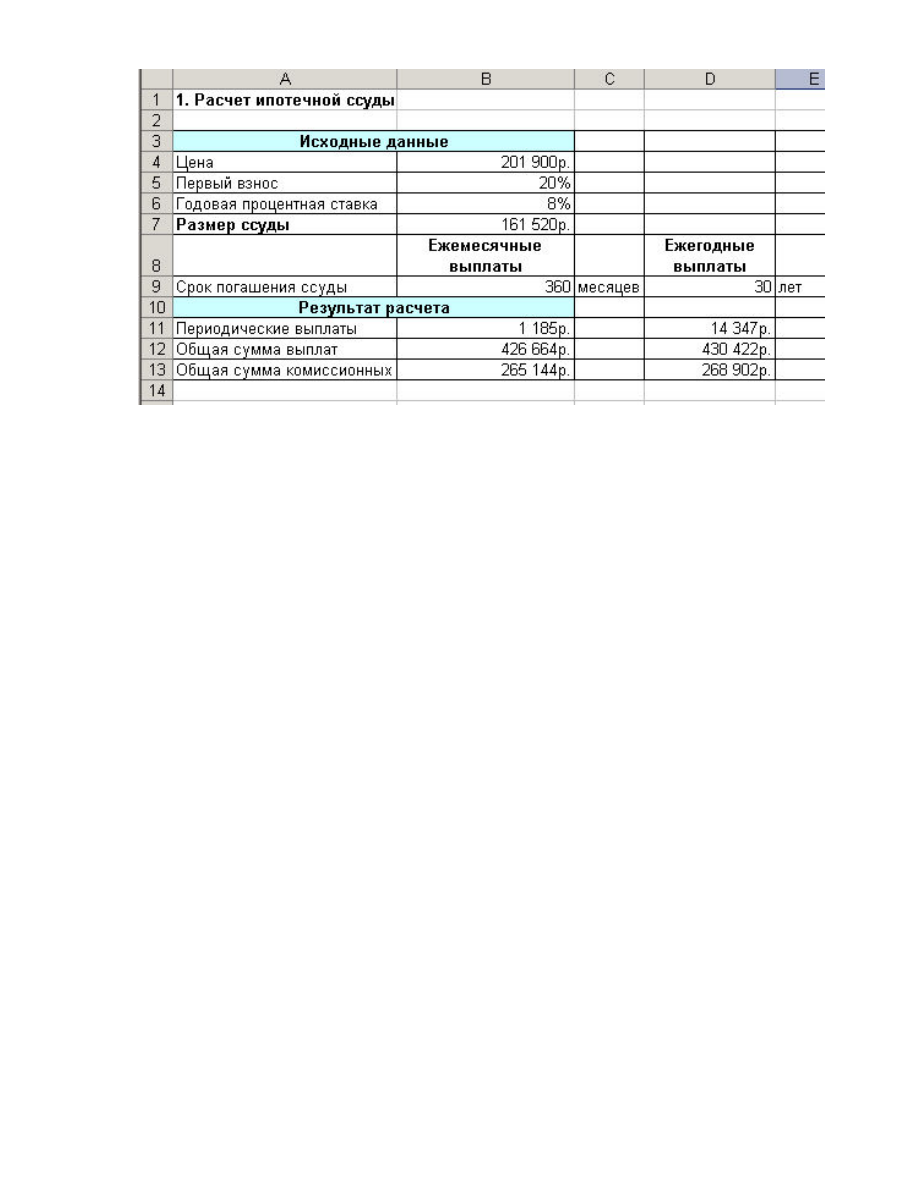
Рис. 3. Расчет ипотечной ссуды.

7
2. Расчет годовой процентной ставки
Функция ЧПС возвращает чистый текущий объем вклада, вычисляемый на основе
ряда последовательных поступлений наличных денег и нормы амортизации.
Чистый текущий объем вклада – это сегодняшний объем будущих платежей (отри-
цательные значения) и поступлений (положительные значения).
Например, вам предлагают следующую сделку. У вас берут в долг некоторую сумму
денег и предлагают через k1 лет вернуть сумму, равную Рk1, через k2 лет – Рk2 и т. д. и, на-
конец, через kn лет – Рkn. Кроме данной сделки, у вас есть альтернативный способ использо-
вания ваших денег, например, положить их в банк под i процентов годовых. Тогда чистым
текущим объемом вклада является та сумма денег, которой вам нужно располагать началь-
ный год, чтобы, положив их в банк под i % годовых, получили предлагаемую прибыль.
Синтаксис: ЧПС(Ставка;Значение1;Значение2;…..)
Аргументы:
ставка – ставка дисконтирования за один период;
значение 1, значение 2, – от 1 до 29 аргументов, представляющих расходы и доходы:
• значение 1, значение 2, … должны быть равномерно распределены во времени,
выплаты должны осуществляться в конце каждого периода.
ЧПС использует порядок аргументов значение 1, значение 2, … для определения по-
рядка поступлений и платежей. Убедитесь в том, что ваши платежи и поступления введены в
правильном порядке.
Считается, что инвестиция, значение которой вычисляет функция ЧПС, начинается за
один период до даты денежного взноса 1-го значения и заканчивается с последним денеж-
ным взносом в списке.
Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый
денежный взнос приходится на начало первого периода, то первое значение следует доба-
вить к результату функции ЧПС, но не включать в список аргументов.
Функция ЧПС связана с функцией ВСД (внутренняя скорость оборота). ВСД – это
скорость оборота, для которой ЧПС равняется нулю:
ЧПС(ВСД(…);…)=0.
Функция ВСД возвращает внутреннюю скорость оборота для ряда последовательных
операций с наличными деньгами, представленными числовыми значениями. Объемы опера-
ций не обязаны быть регулярными, как в случае ренты.
Внутренняя скорость оборота – это процентная ставка дохода, полученного от ин-
вестиций, состоящих из выплат (отрицательные значения) и поступлений (положительные
значения), которые происходят в регулярные периоды времени.
Синтаксис: ВСД (Значения;Предположение).
Аргументы:
значения – массив или ссылка на ячейки, содержащие числовые величины, для кото-
рых вычисляется внутренняя ставка доходности. Значения должны включать, по
крайней мере, одно положительное значение и одно отрицательное значение, для того
чтобы можно было вычислить внутреннюю скорость оборота.
Функция ВСД использует порядок значений для интерпретации порядка денежных выплат
или поступлений, поэтому нужно следить, чтобы значения выплат и поступлений вводились
в правильном порядке.
предположение – величина, о которой предполагается, что она близка к результату
ВСД.

8
Для вычисления ВСД Excel использует метод итераций. Начиная со значения про-
гноз, функция ВСД выполняет циклические вычисления, пока не получит результат с точно-
стью 0,00001. Если функция ВСД не может получить результат после 20 попыток, то воз-
вращается значение ошибки #ЧИСЛО!
В большинстве случаев нет необходимости задавать прогноз для вычислений с помо-
щью функции ВСД. Если прогноз опущен, то он полагается равным 0,1 (10 %).
Если ВСД выдает значение ошибки #ЧИСЛО! Или результат далек от ожидаемого,
можно попытаться выполнить вычисления еще раз, но уже с другим значением аргумента
прогноз.
Задание 2. Вас просят в долг 10000 руб. и обещают вернуть через год 2000 руб., через
два года – 4000 руб., через три года – 7000 руб. При какой годовой процентной ставке эта
сделка выгодна?
Решение.
1. Откройте Лист 2 и переименуйте его в Задание 2.
2. Введите в ячейки A1:B7 данные, представленные на рис. 4.
Рис. 4. Форма для расчета годовой процентной ставки
3. Для выполнения расчетов в ячейки должны быть введены формулы, показанные на
рис. 5.
Рис. 5. Формулы для расчета годовой процентной ставки
9
4. Первоначально в ячейку В10 введите произвольный процент, например 3 %.
В ячейку В11 введите формулу =ЧПС(В10;В5:В7) (см. рис. 5).
5. В ячейку С8 введите формулу:
=ЕСЛИ(В8=1;»год»;ЕСЛИ(И(В8>=2;B8<=4) ;»года»;»лет»))
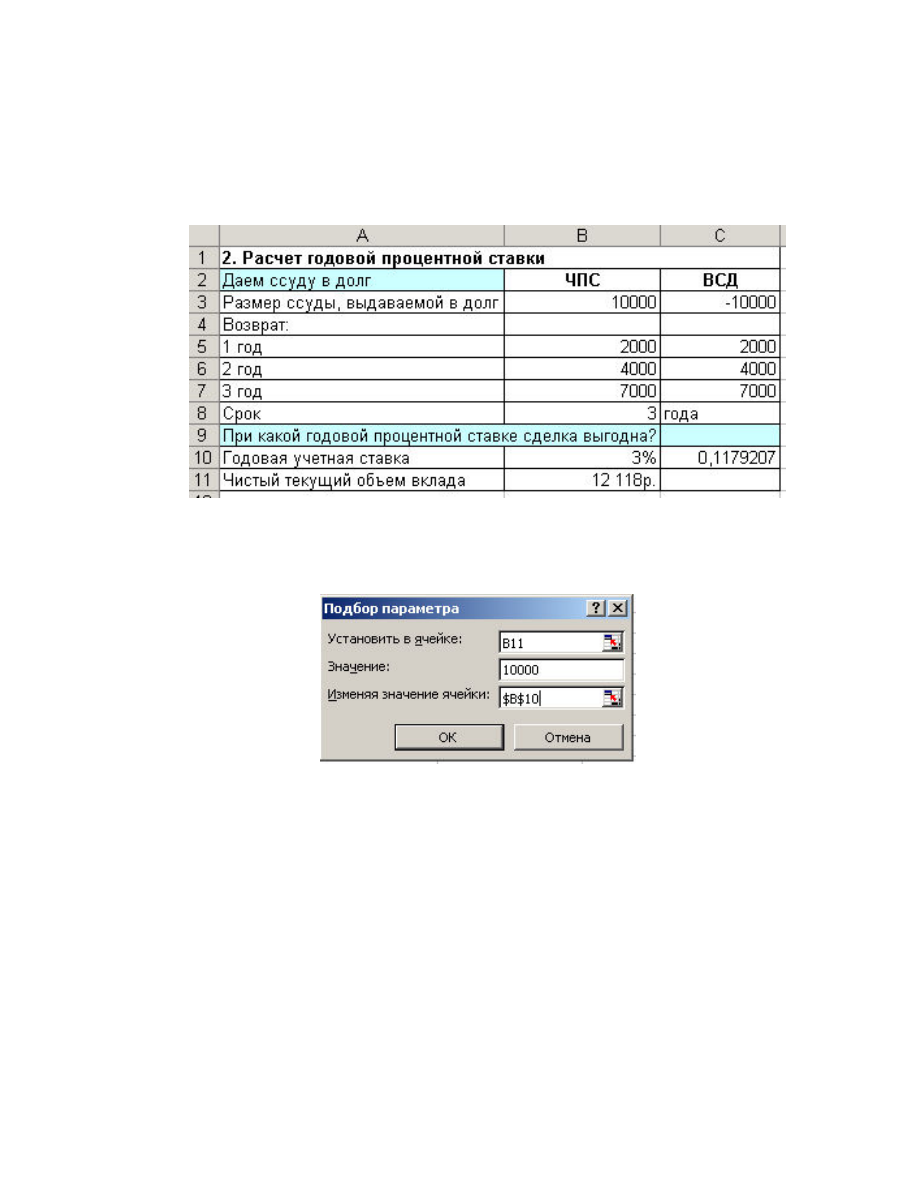
В результате должно получиться (см. рис. 6):
Рис. 6. Расчет чистого текущего объема вклада
6. Затем выбираем команду Сервис / Подбор параметра
и заполняем открывшееся диалоговое окно Подбор параметра, как показано на рис. 7.
Рис. 7. Диалоговое окно Подбор параметра при расчете
годовой процентной ставки
7. В поле Установить в ячейке: укажите ссылку на ячейку В11, в которой вычисляется
чистый текущий объем вклада по формуле:
=ЧПС(B10;B5:B7).
В поле Значение установить 10000 – размер ссуды.
В поле Изменения значения ячейки укажите ссылку на ячейку В10, в которой вычис-
ляется годовая процентная ставка.
После нажатия кнопки ОК средство подбора параметров определит, при какой годо-
вой процентной ставке чистый текущий объем вклада равен 10000 руб. Результат вычисле-
ния выводится в ячейку В10.
8. В нашем случае годовая учетная ставка равна 11,79 %.
Вывод: если банки предлагают большую годовую процентную ставку, то предла-
гаемая сделка не выгодна.
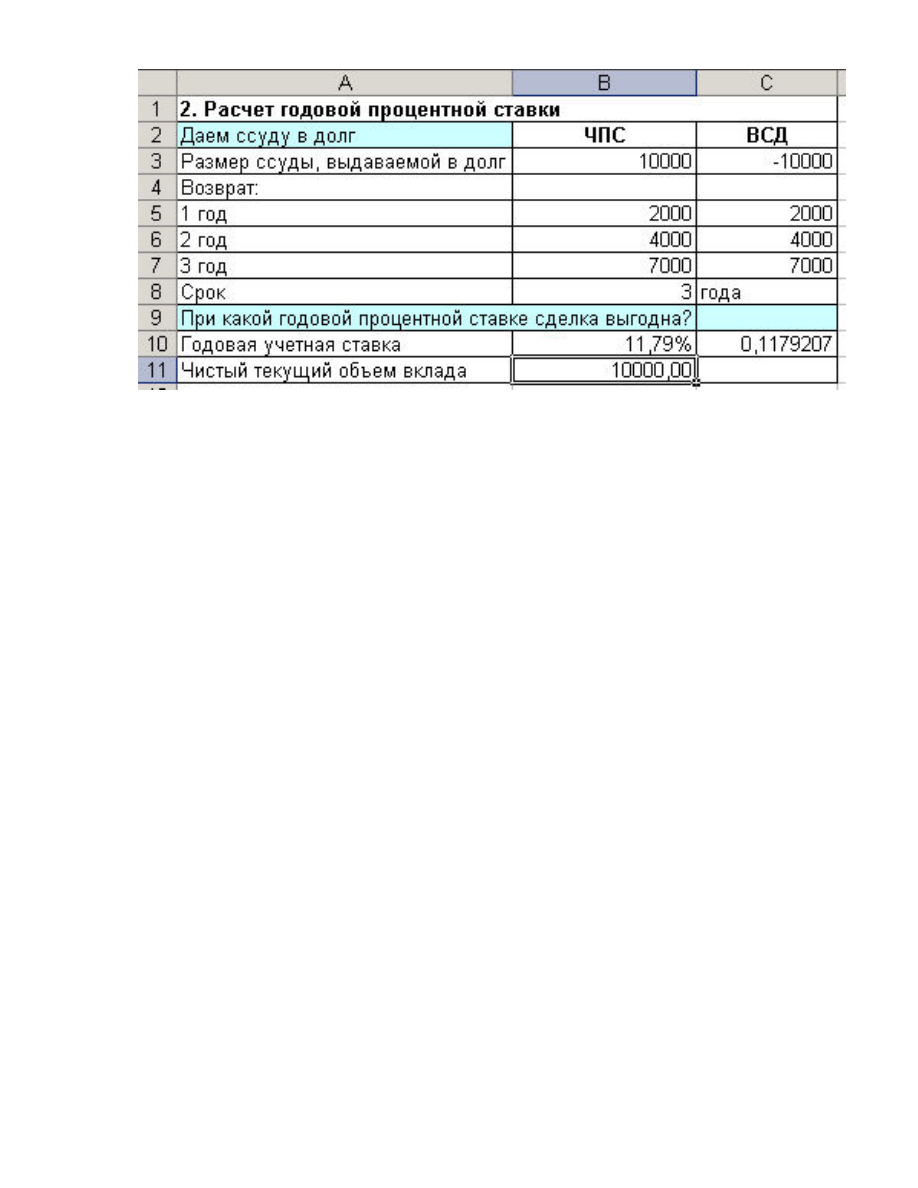
9. Результаты расчеты должны быть следующими:
10
Рис. 8. Расчет годовой процентной ставки
3. Расчет эффективности капиталовложений
Расчет эффективности капиталовложений осуществляется с помощью функции ПС.
Функция ПС возвращает текущий объем вклада на основе постоянных периодиче-
ских платежей.
Функция ПС аналогична функции ЧПС. Основное различие между ними заключается
в том, что функция ПС допускает, чтобы денежные взносы происходили либо в конце, либо
в начале периода. Кроме того, в отличие от функции ЧПС, денежные взносы в функции ПС
должны быть постоянными на весь период инвестиции.
Синтаксис: ПС(Ставка;Кпер;Плт;Бс;Тип)
Аргументы:
Ставка – процентная ставка за период,
Кпер – общее число периодов платежей по аннуитету,
Плт – выплата, производимая в каждый период и не меняющаяся за все время выпла-
ты ренты. Обычно выплаты включают основные платежи и платежи по процентам, но
не включают других сборов или налогов,
Бс – требуемое значение будущей стоимости или остатка средств после последней
выплаты. Если аргумент опущен, он полагается равным 0 (будущая стоимость займа,
например, равна 0),
Тип – число 0 или 1, обозначающее, когда должна производиться выплата.
Задание 3. У вас просят в долг 10000 руб. и обещают возвращать по 2000 руб. в течение 7
лет. Будет ли выгодна эта сделка при годовой ставке 7 %?
Решение:
1. Откройте Лист 3 и переименуйте его в Задание 3.
2. Введите в ячейки A1:B6 данные, представленные на рис. 9.