Файл: ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ В ЭКОНОМИКЕ.pdf

21

Аргументы:  

  Ставка – процентная ставка за период, 
  Плт – величина постоянных периодических платежей,  
  Пс – текущее значение, т.е. общая сумма, которую составят будущие платежи,  
  БС  –  будущая  стоимость  или  баланс  наличности,  который  нужно  достичь  после  по-

следней выплаты. 
Если  аргумент  БС  опущен,  он  полагается  равным  0  (например,  будущая  стоимость 

займа  равна  0),  тип  –  число  0  или  1,  обозначающее,  когда  должна  производиться  выплата. 
Если тип равен 0 или опущен, то оплата производится в конце периода, если 1 – то в начале 
периода. Если тип = 0 и БС = 0 функция КПЕР вычисляется по формуле (7): 

(7) 

где Р – ПС; i – Ставка; А – Плт. 
 
 
 
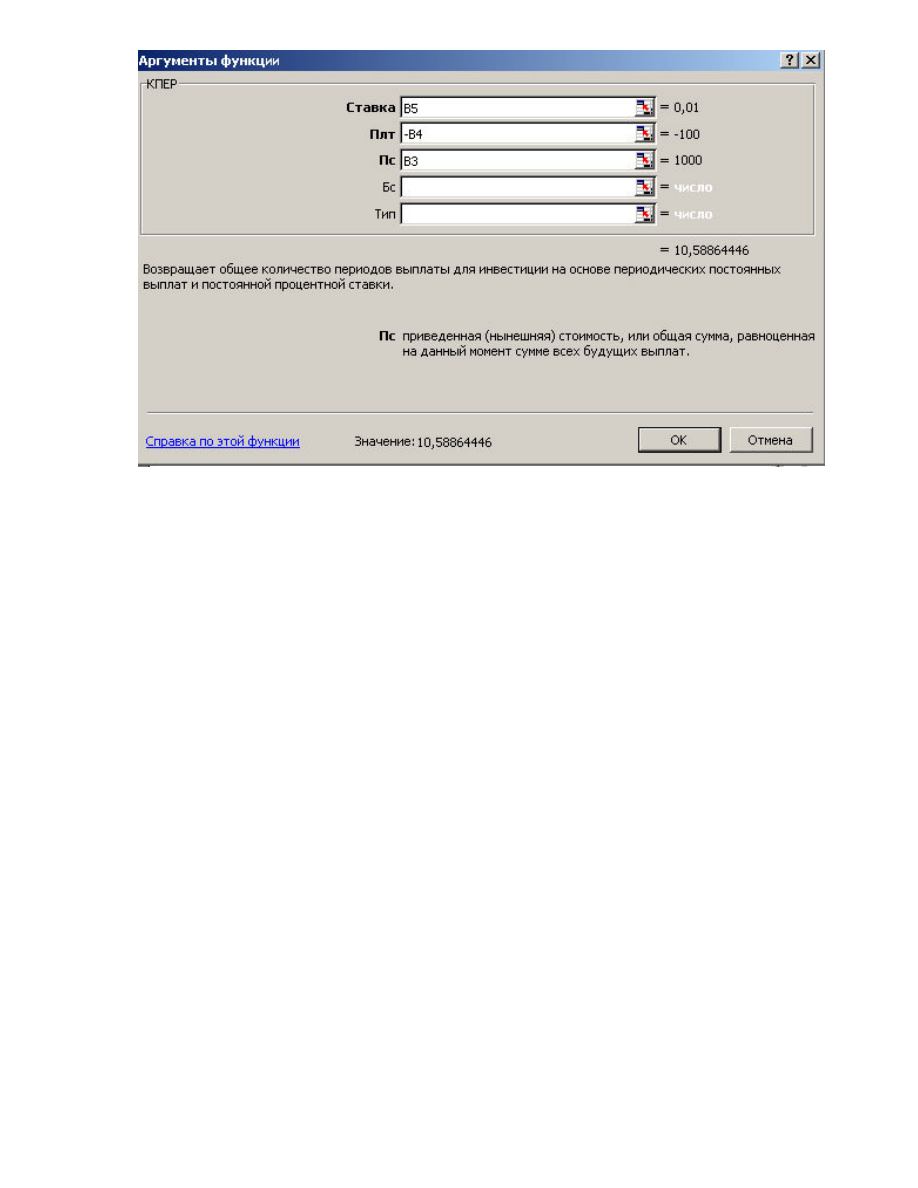
Задание 6. Вы берете в долг 1000 руб. при годовой ставке 1% и собираетесь выплачивать по 
100 руб. в год, Какое будет число выплат долга?  
 
Решение: 

1.  Откройте Лист 6 и переименуйте его в Задание 6. 
2.  Ведите данные в ячейки А1:В6 (см. рис. 17). 
 

Рис. 17. Расчет количества периодов выплат 

3.  В ячейку В6 введите формулу: 

=КПЕР(B5; -B4; B3) 

 
В результате получаем ответ: ≈11. (см. рис. 18). 
 

22

Рис. 18. Диалоговое окно Аргументы функции КПЕР 

23

Вычисление процентной ставки 
 

Функция СТАВКА вычисляет процентную ставку, необходимую для получения оп-

ределенной суммы в течение заданного срока путем постоянных взносов, за один период.  

Следует  отметить,  что  функция  СТАВКА  вычисляет  процентную  ставку  методом 

итераций, поэтому решение может быть и не найдено. Если после 20 итераций погрешность 
определения ставки превышает 0,0000001, то функция СТАВКА возвращает значение ошиб-
ки #ЧИСЛО! 
 
Синтаксис: СТАВКА(КПЕР; Плт; Пс; БС; Тип; Предположение). 
Аргументы:  

  КПЕР – общее число периодов платежей по аннуитету; 
  Плт – регулярный платеж (один раз  в период), величина которого  остается постоян-

ной в течение всего срока аннуитета. Обычно Плт состоит из платежа основной сум-
мы и платежа процентов, но не включает других сборов или налогов. Если аргумент 
опущен, должно быть указано значение аргумента БС; 

  Пс – приведенная к текущему моменту стоимость или общая сумма, которая на теку-

щий момент равноценна ряду будущих платежей;  

  БС  –  требуемое  значение  будущей  стоимости  или  остатка  средств  после  последней 

выплаты.  Если  аргумент  БС  опущен,  то  он  полагается  равным  0  (например,  БС  для 
займа равно 0); тип – число 0 или 1, обозначающее, когда должна производиться вы-
плата; предположение – предполагаемая величина ставки. 
Если БС = 0 и тип = 0, функция СТАВКА является корнем уравнения (8): 

(8) 

 
 
Задание 7. Определить процентную ставку для четырехлетнего займа размером в 8000 руб. с 
ежемесячной выплатой 200 руб. 
 
 
 
Решение: 

1.  Откройте Лист 7 и переименуйте его в Задание 7. 
2.  Ведите данные в ячейки А1:В7 (см. рис. 19). 
 

Рис. 19. Расчет процентной ставки 

3.  В ячейку В6 введите формулу: 
 

=СТАВКА(B5*12;-B4;B3). 

24

4.  В ячейку В7 введите формулу: 
 

= В6*12. 

 
В результате получаем: месячная (так как период равен месяцу) процентная ставка равна 
0,77 %. Процентная ставка годовая равна 9 % см. рис 20). 

Рис.20. Результаты вычисления процентной ставки