Файл: МУ к курсовой автоматизация технологических процессов.doc

Мощность резания, кВт,

(0)

Мощность подачи, кВт,

(0)

Поскольку скорость подачи во много раз меньше скорости резания, мощность подачи намного меньше мощности резания и составляет относительно последней 1 — 0,1 %.

Р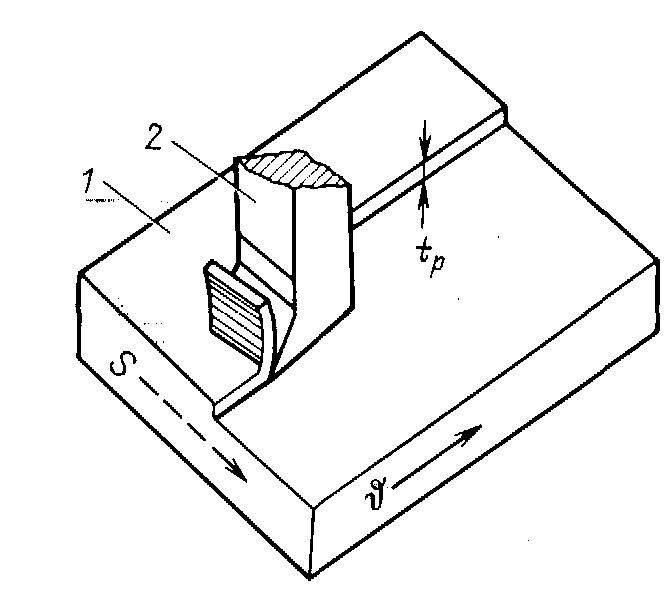
асточка применяется для черновой, чистовой и алмазной обработок отверстий на токарных и расточных станках. При расточке резцы, оснащенные пластинками из быстрорежущей стали, твердых сплавов или из ограненного технического алмаза, закрепляют в оправках. Ско­рость, силу и мощность резания при черновой и чистовой расточках определяют по тем же формулам (2) -- (6), что и для точения.

С

Рис. 3. Схема строгания

Перемещение резца за один двойной ход стола перпендикулярно главному движению называется движением подачи х, мм/мин. Вели­чина /р, на которую углубляется резец в изделие при одном проходе, называется глубиной резания. Перемещение траверсы и суппортов, подъем резца при обратном ходе, установочные медленные перемеще­ния стола относятся к вспомогательным движениям.

Скорость, усилия и мощность резания при строгании определяют по тем же формулам (1) - (3), что и для точения.

Сверление (рис. 4) осуществляется за счет вращательного (глав­ного) движения инструмента - сверла 1 (иногда детали) и его про­дольного перемещения в детали 2 - движения подачи. Продольное и поперечное перемещения стола, перемещение шпиндельной бабки, за­жим колонны являются вспомогательными движениями.

Окружную скорость на периферии сверла v, м/мин, называют ско­ростью резания при сверлении. Перемещение сверла вдоль своей оси за один оборот определяет подачу. Скорость резания при сверлении нахо­дят по эмпирической формуле

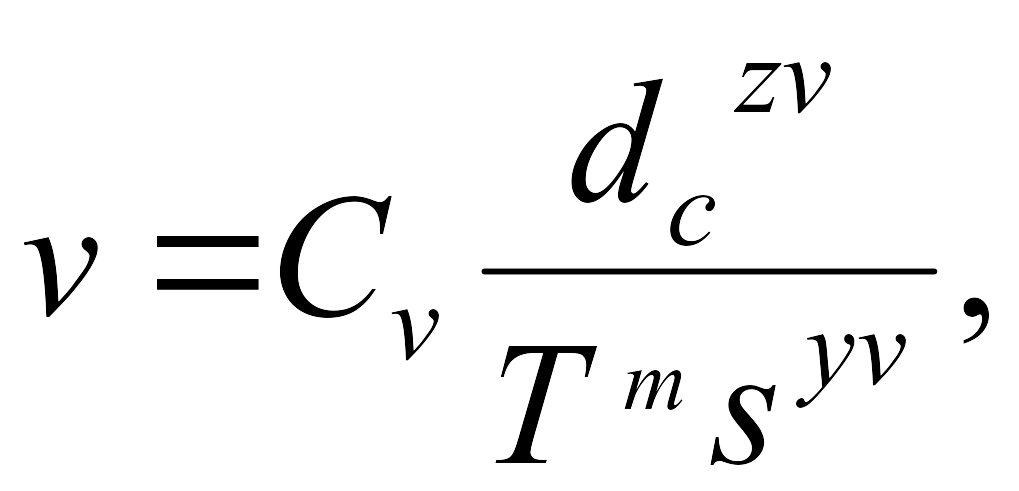(0)

где С_v -- коэффициент, зависящий от материала детали и сверла; d_c -- диаметр сверла, мм; Т - стойкость сверла, мин; s -- подача, мм/об; у_v,, z_v, т -- показатели степени, зависящие от материала детали и диа­метра сверла.

Вращающий момент, Нм, при сверлении определяют по эмпиричес­кой формуле

(0)

откуда, зная угловую скорость сверла, рассчитывают мощность реза­ния, кВт:

(0)

Сила, Н, преодолеваемая механизмом подачи при сверлении, также оп­ределяется по эмпирической формуле:

(0)

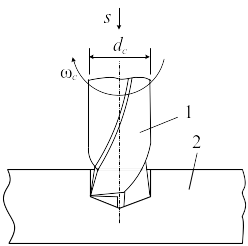
Рис. 4. Схема сверления

Все коэффициенты и показатели сте­пени, входящие в эмпирические форму­лы, приводятся в справочниках по ре­жимам резания

Фрезерование (рис. 5) производит­ся вращающейся фрезой 1, имеющей несколько режущих лезвий — зубьев, каждое из которых за счет поступатель­ного перемещения фрезы относитель­но детали 2 снимает стружку в преде­лах определенного угла поворота фре­зы, а затем вращается вхолостую. Главным движением при фрезеровании является вращение фрезы, перемещение детали относительно инструмен­та представляет движение подачи. Быстрое перемещение стола, на кото­ром укреплена деталь, и ускоренное перемещение шпиндельной бабки при наладке относятся к вспомогательным движениям.

Под скоростью резания, v, м/мин, понимают окружную скорость на периферии фрезы, которую определяют по эмпирической формуле

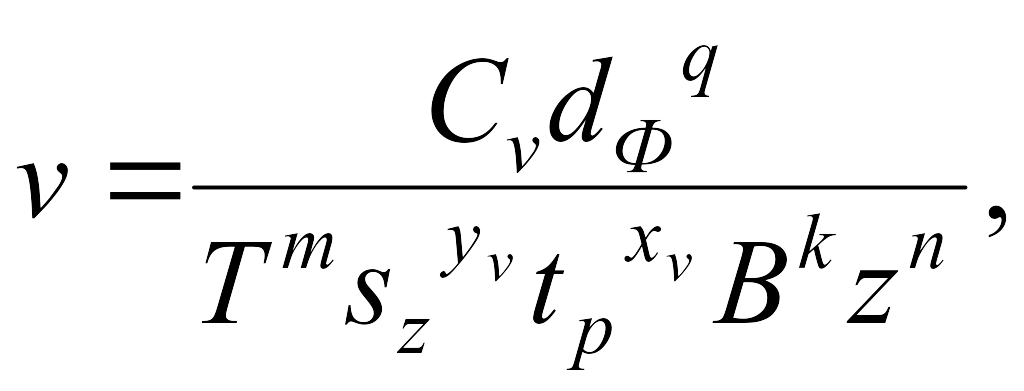(0)

где С_v,q, т, п., х_v, у_v, k — коэффициент и показатели степени, завися­щие от материала детали и фрезы, вида обработки и охлаждения; d_Ф -- диаметр фрезы, мм; s_z -- подача на зуб фрезы, мм; В — ширина фре­зерования, мм; z -- число зубьев фрезы.

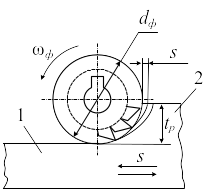
Рис. 5. Схема фрезерования

Усиление резания, Н, определяют по выражению

(0)

Мощность резания, кВт, рассчитывают по формуле

(0)

где n_ф — частота вращения фрезы, n_ф = 30_Ф/.

Все коэффициенты и показатели степени в (12) и (14) приводят­ся в справочниках по режимам резания.

Шлифование (рис. 6) производится, как правило, абразивными кругами, при этом каждое абразивное зерно в зоне обработки рабо­тает как резец, снимая стружку с детали в пределах определенного угла поворота. Главное движение при шлифовании — вращение шли­фовального круга 1; поступательное перемещение круга относитель­но детали 2 представляет движение подачи.

Различают плоское шлифование (рис. 6, д, б), при котором обраба­тывается плоская поверхность, и круглое шлифование (рис. 6, в, г), при котором обрабатывается поверхность тела вращения. Плоское шлифование может осуществляться периферией (рис. 6, д) или тор­цом (рис. 6, б) шлифовального круга 1.

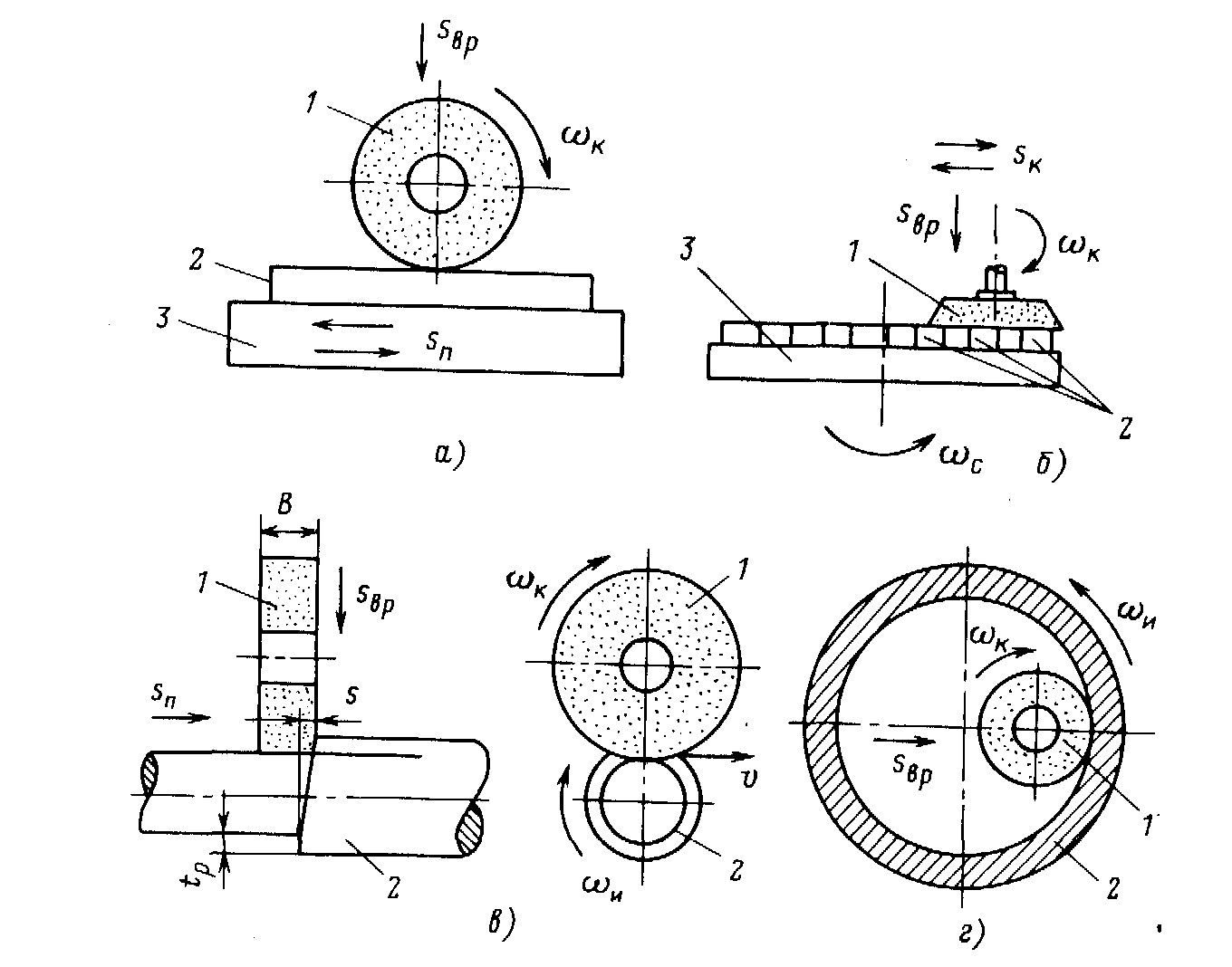
Рис. 6. Схема шлифования на станках

а — плоскошлифовальном с прямоугольным столом; б — плоскошлифоваль­ном с круглым столом; в — круглошлифовальном; г — внутришлифовальном; 1 - шлифовальный круг; 2 - деталь; 3 - стол (магнитная плита)

Стол 3, на котором устанав­ливается магнитная плита для крепления деталей 2, может иметь прямо­угольную и круглую формы. На шлифовальных станках с прямоуголь­ным столом (рис. 6, а) последний совершает возвратно-поступатель­ное движение (продольная подача s_п), периодическое дозированное перемещение (поперечная подача s_п,п) и перемещение на врезание s_вр. На шлифовальных станках с круглым столом (рис. 6, б) одним из движений подачи является вращение деталей с магнитной плитой и столом со скоростью _с. Другое движение подачи - перемещение s_к шлифовального круга в радиальном направлении относительно стола, а также перемещение на врезание s_вр.

Выбор режимов резания при шлифовании определяется по технологическим таблицам, составленным на основании эмпирических данных.

При круглом наружном (рис. 6, в) и внутреннем (рис. 6, г) шлифованиях изделие получает вращение со скоростью _и как пра­вило, в сторону, противоположную вращению шлифовального круга. Относительное перемещение шлифовального круга вдоль оси враще­ния детали представляет продольную подачу s_п.

Скорость резания при шлифовании v, м/с, определяется окружной скоростью шлифовального круга и равна примерно 20—80 м/с. При этом допускаются небольшие глубины шлифования t_р, равные 0,05— 0,005 мм. Все большее применение стало находить силовое шлифо­вание, обеспечивающее значительную глубину шлифования — до 10 мм.

В процессе шлифования абразивные зерна притупляются, что при постоянной подаче влечет за собой увеличение мощности шлифова­ния и образование прижогов на поверхности детали. Для устранения этих явлений круг правят, срезая слой абразива и вводя в работу зер­на с новыми режущими кромками. Время работы круга между двумя последовательными правками характеризует его стойкость Т, мин.

При плоском шлифовании периферией круга на станках с прямо­угольным столом стойкость может быть рассчитана по формуле

(15)

где С_v — коэффициент, зависящий от скорости резания; s_П^— скорость движения стола (продольная подача), м/мин; s_ПП— попереч­ная подача в долях ширины шлифовального круга; sвр -- подача на врезание на ход стола, мм/ход; k1, k2 — коэффициенты, зависящие от обрабатываемого материала и диаметра шлифовального круга.

Расчет гидропривода для наложения давления на кристаллизующийся металл

Одной из серьезных проблем при производстве металлопродукции с более высоким уровнем химических и физико-механических свойств является формирования однородной структуры литых заготовок и изделий в сечениях толщиной 50…100 мм и более.

Установлено, что управление формированием структуры можно осуществлять, накладывая на кристаллизующийся металл давление по закону, согласованному со скоростью кристаллизации [12].

Речь идет о наложении давления на уровне 300…400 МПа с компенсацией усадки в пределах 10…15 % в течение отрезка времени 5…10 с при опрессовке заготовок из сплава В95 массой 2,8 кг. Мощность гидропривода при этом составляет N = pQ/612 кВт. Здесь Q, л/мин; p, кгс/см². Это соответствует установленной мощности применяемого гидропривода, если принимать во внимание усредненные величины. В переходных же процессах, как показали выполненные исследования, давление в рабочей полости гидроцилиндра изменяется по сложной зависимости (рис.16).

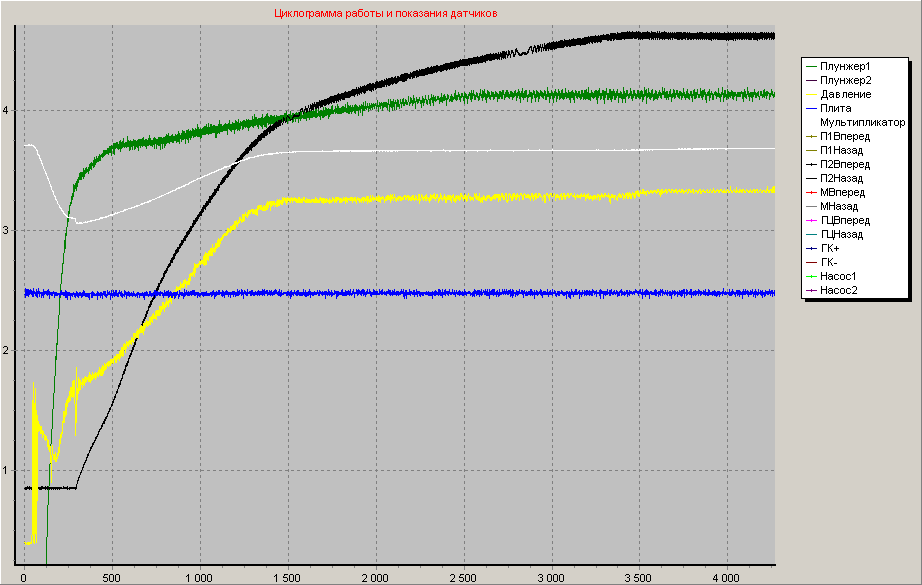
Рис.16. Осциллограммы, иллюстрирующие свойства жидкого металла под давлением как объекта автоматического управления (Желтым цветом показано изменение давления в полости гидроцилиндра от 0 до 10 МПа, зеленым – движение правого, черным – левого гидроцилиндра в пределах от 0 до 125 мм)

В начале процесса, когда включается в работу правый гидроцилиндр, давление в рабочей полости гидроцилиндра нарастает достаточно быстро, но в момент включения левого гидроцилиндра (рис.17) давление падает до 30 МПа. Далее давление нарастает, но не мгновенно, поэтому скорость наложения давления приобретает вполне определенное значение, которое зависит от производительности гидронасоса. Если по ходу технологического процесса возникает необходимость включить параллельно другой гидроцилиндр (2), то давление в гидросистеме, не достигнув номинального значения 10 МПа, снова падает до 20 МПа, и, если требуется подать на кристаллизующийся металл максимальное усилие пресса, гидросистема в этом режиме не способна адекватно реагировать на управляющее воздействие.

Отсюда следует, что используемая для производства литых заготовок, указанных выше размеров, гидросистема не обладает необходимыми динамическими свойствами.

Возможны следующие варианты решения данной задачи:

• увеличить производительность насоса;

• установить гидроаккумулятор;

• использовать мультипликатор в режиме аккумуляции энергии.

Кроме того, просматриваются и гибридные схемы.

В целях отработки наилучшего решения предлагается разработать математическую модель и соответствующую ей структуру системы управления.

Представленная на рис.17 схема учитывает динамику гидроцилиндра (инерционная нагрузка, сила трения, полезная нагрузка развиваемая сила, расход, сжимаемость масла), гидрораспределителя (устройство управления расходом и перепадом давления в цилиндре) и кинематических цепей (чувствительные и сравнивающие элементы), а также представляет структуру системы управления.

насыщение по расходу и давлению не происходит;

положение рабочего органа соответствует среднему положению поршня в цилиндре;

перетечками в цилиндре и в АРС пренебрегают.

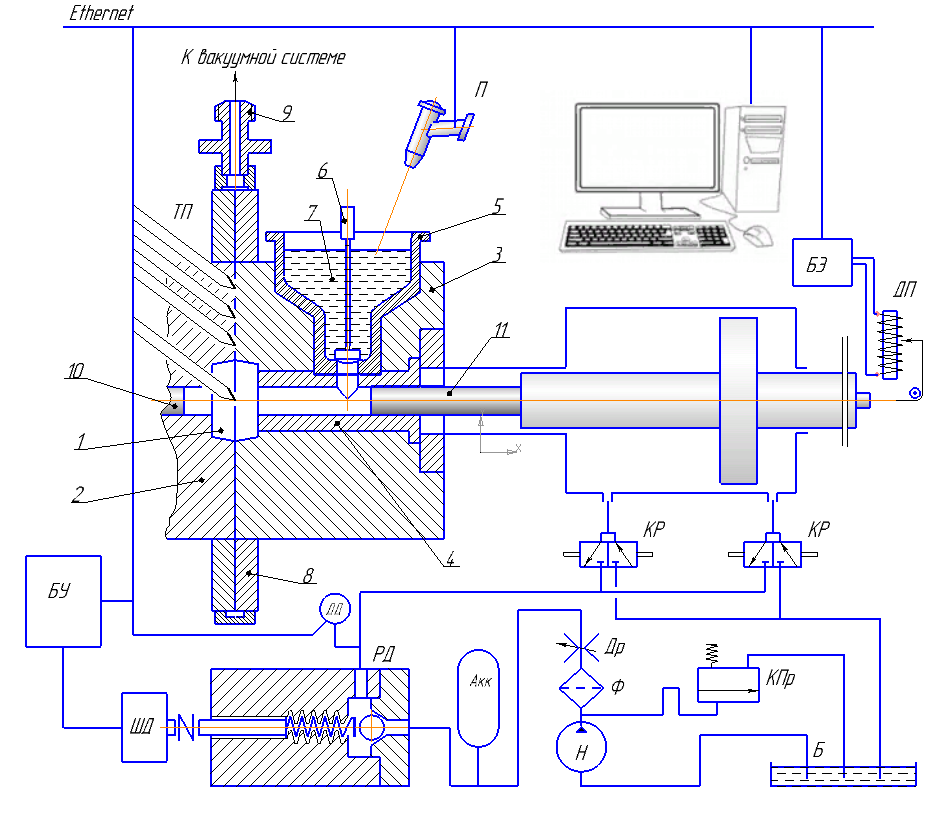
Рис.17. Структурная и гидрокинематическая схема управления процессом наложения давления

Обозначения: 1-заготовка; 2,3- форма; 4-втулка; 5-чаша заливочная; 6-стопор; 7-жидкий металл; 8-кольцо-бандаж формы; 9-штуцер; 10,11- плунжеры прессующие; Акк - аккумулятор; Б – бак; БУ – блок управления; БЭ – блок управления; ДД – датчик давления; ДП – датчик положения поршня; Др – дроссель; КПр – клапан предохранительный; КР - клапан распределительный; РД – регулятор давления; Н – насос; ШД – шаговый двигатель; Ф – фильтр

Математическая модель гидропривода

При составлении уравнении движения привода сделаны следующие допущения:

функции, описывающие расходные и силовые характеристики элементов привода, непрерывны;

динамикой задающего электродвигателя пренебрегают;

давление в напорной магистрали постоянно;

давлением слива пренебрегают;

люфты и упругость в передаточных цепях АРС отсутствуют;

В соответствии со 2-м законом Ньютона уравнение движения поршня и штока гидроцилиндра

M d²x/dt² = F(p₁ – p₂) – Σ T -R, (17)

где М — масса поршня и штока, кг; х — перемещение поршня, м; F — площадь поверхности поршня, м²; р₁, р₂ — давления в полостях цилиндра, Па; Σ Т — суммарная сила трения в направляющих и уплотнениях штока, Н; R — полезная нагрузка, Н.

Уравнения неразрывности потоков рабочей жидкости с учетом ее сжимаемости в полостях цилиндра имеют следующий вид:

Q₁ = Fx + p₁V₁/E;

Q₂ = Fx + p₂V₂/E; (18)

где Q₁ и Q₂ — расходы рабочей мощности, идущей в полость l и сливающейся из полости 2 гидроцилиндра, м³; V₁ = Fx — объем полости гидроцилиндра, м³;V₂ = F( L – x), где L — длина хода поршня, м; Е= 1,5∙10⁹ Па—модуль упругости рабочей жидкости. Условие замыкания привода обратной связью:

Fx + p₁V₁/E = μ y √2(p_н – p₁)/ρ , (19)

где у – смещение шарика регулятора, мм.

Отсюда

y = (Fx + p₁V₁/E)/ μ √2(p_н – p₁)/ρ

На основании выражений (17)-(19) запишем систему уравнений, описывающих движение привода:

M d²x/dt² = F(p₁ – p₂) – Σ T –R;

Q₁ = Fx + p₁V₁/E; (20)

Q₂ = Fx + p₂V₂/E;

y = (Fx + p₁V₁/E)/ μ √2(p_н – p₁)/ρ.

Расход масла через открытое отверстие регулятора и КР определяется по формулам:

Q_{1 =} μ y √2(p_н – p₁)/ρ; (21)

Q_{2 =}  b √2p₂/ρ.

где  - переменный коэффициент расхода; y—ширина щели открытого отверстия регулятора, м; р_н — давление в напорной линии, р_н = 10 МПа;  = 900 кг/м³ — плотность рабочей жидкости,  - постоянный коэффициент расхода клапана распределительного (КР) , b - ширина щели КР .

Движение привода при установившейся скорости описывается алгебраическими уравнениями, полученными из формул (6), (7) в результате приравнивания к нулю соответствующих производных (значения величин при установившейся скорости — с индексом «ноль»):

F(p₁₀ – p₂₀) = Σ T₀ –R₀;

Q_{10 =} μ₀ y₀ √2(p_н – p₁₀)/ρ;

Q_{20 =}  b √2p₂₀/ρ; (22)

y = (Fx + p₁V₁/E)/ μ √2(p_н – p₁)/ρ.

Для анализа динамических характеристик привода, в том числе для определения областей устойчивой работы, необходимо провести линеаризацию уравнений (20), (21). Смысл ее заключается в представлении нелинейных функций в виде линейных в окрестностях заданной точки [в нашем случае в окрестностях точки, характеризующей установившееся движение привода по формуле (22).

Линеаризуя уравнения (22) для расхода рабочей жидкости, обозначив и введя коэффициент

K_y = 0,5∙10^-4  p_н

получим:

Q₁ = Q₀ + K_уΔy;

Q₂ = Q₀ + K_уΔy. (23)

где К_у — коэффициент усиления регулятора, характеризующий возрастание расхода при увеличении рабочего зазора.

Подставив уравнение (18) в систему уравнений (22) и проведя линеаризацию для других переменных, получим:

M (d²x₀ + Δx)/dt² = F(p₁₀ + Δp₁ – p₂₀ - Δp₂) – λd(x₀ + Δx)/dt – R₀ –ΔR;

d(p₁₀ + Δp₁)dt = E/V [Q₀ + K_yΔy - K_р Δp₁ – Fd(x₀ + Δx)/dt]; (10)

d(p₂₀ + Δp₁)dt = E/V [Fd(x₀ + Δx)/dt – Q₀ - K_yΔy + K_р Δp₂] - Fd(x₀ + Δx)/dt];

Q₁ = Q₀ + K_уΔy - K_р Δp₁ ;

Q₂ = Q₀ + K_уΔy - K_р Δp₂ ;

Δy = (Fx + Δp₁V₁/E)/ μ √2(p_н – Δp₁)/ρ.

Здесь λ= ΣT/dt/dx - коэффициент вязкого трения в направляющих и уплотнениях штока (для станочных гидроприводов можно принять λ=1,5∙10⁴кг/с).

Обозначим перепад давления в полостях гидроцилиндра через Δp, вычтем из второго третье уравнение системы (10), получим:

M (d²Δx)/dt² =FΔp – ΣT – ΔR;

d(p₁₀ + Δp₁)dt = E/V [K_yΔy – Fd( Δx)/dt];