ΔQ₁ = Q₀ + K_уΔy; (24)

Δy = (Fx + Δp₁V₁/E)/ μ √2(p_н – Δp₁)/ρ.

Составление структурной схемы и определение областей устой­чивости управления ГП с АРС

Структурная схема привода, соответствующая системе уравнений (24), показана на рис. 18. Схема позволяет наглядно показать взаимосвязь элементов привода с помощью следующих передаточных функций.

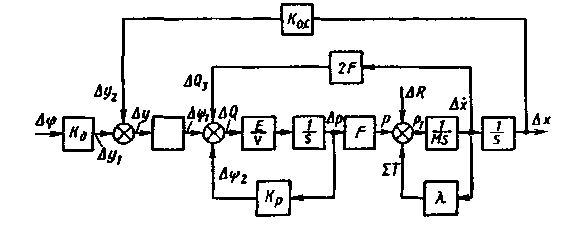
Рис. 18. Структурная схема ГП с АРС

Угол поворота ШД преобразуется в смещение золотника:

Смещение золотника из нейтрального положения приводит к увеличению объема масла, поступающего в полость гидроцилиндра и вытесняемого из нее.

Часть этого объема идет на сжатие масла:

а возникший перепад давления, воздействуя на площадь поршня F, создает силу Р, которая затрачивается на преодоление сил инерции движущихся масс:

трения в направляющих и уплотнениях штока:

и полезной нагрузки R.

Расход масла, затрачиваемый на перемещение (х) штока, характеризуется звеном

а жесткая отрицательная обратная связь между штоком исполнительного цилиндра и золотником гидроусилителя — звеном

После преобразования структурной схемы по правилам, известным из теории автоматического управления, получаем передаточную функцию разомкнутой системы

(25)

г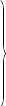 де К - коэффициент усиления; Т - постоянная времени; ξ - коэффициент демпфирования, эти коэффициенты связаны с параметрами привода из уравнений (11) следующим образом:

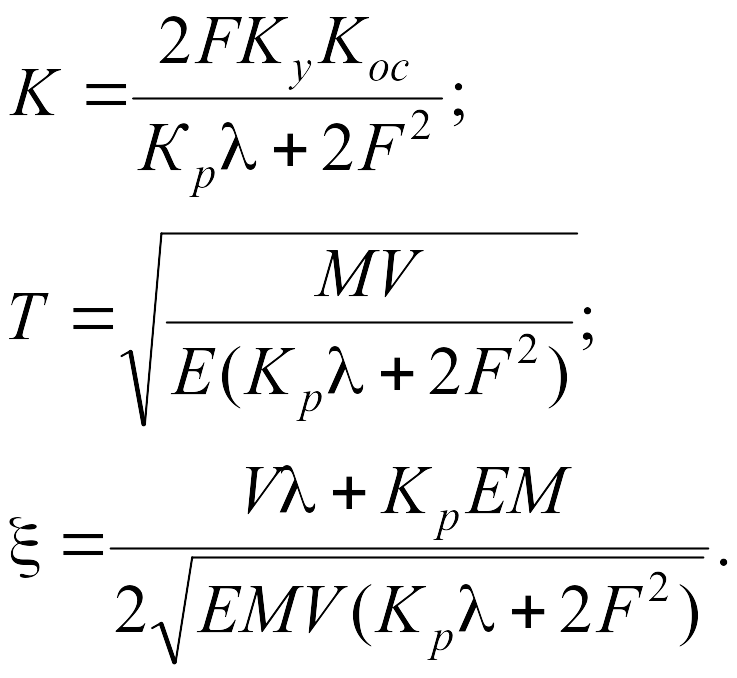(26)

Передаточная функция замкнутой системы, охваченной обратной связью с учетом 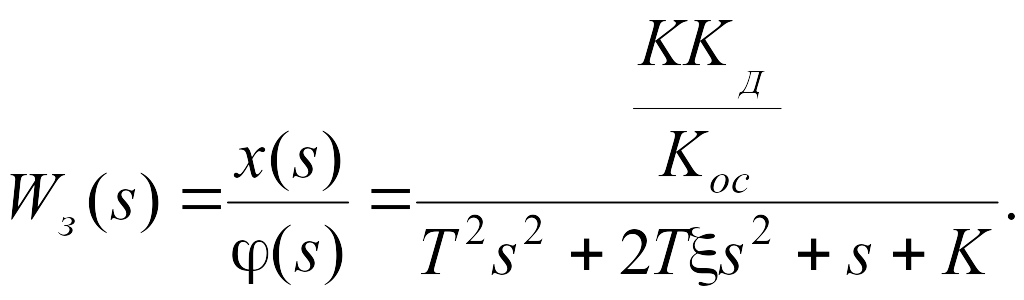(27):

(27)

Для анализа устойчивости ЛЭГП с АЗП применяем алгебраический критерий Рауса—Гурвица для знаменателя выражения (29), откуда находим

(28)

Подставив в формулу (15) выражения для К, Т и ξ из выражения (28) и пренебрегая величиной К_рλ по сравнению с 2F², получим следующий критерий устойчивости для линейных приводов:

(29)

В полученное неравенство входят три слагаемых, зависящих от динамических коэффициентов λ, К_р и К_у линеаризованных характеристик трения рабочего органа и расхода гидрораспределителя, а также от ряда конструктивных параметров F, L, М, К_ос привода, причем первые два слагаемых повышают, а третье — снижает устойчивость.

Таким образом, неравенство (29) определяет область возможных соотношений основных параметров привода, обеспечивающих отсутствие автоколебаний, и будет использовано в дальнейшем при разработке методики расчета ГП с АРС.

На основании приведенных выше зависимостей разработана инженерная методика расчета привода.

Исходными данными для расчета являются: масса рабочего органа (М), длина хода (L), требования к точности позиционирования (ε), диапазону скоростей (v_min - v_max), тяговой силе (R), жесткости (J), скоростной ошибке (ε_ск).

Цель расчета — выбор площади F поршня гидроцилиндра и подведенного давления.

Расчет состоит из нескольких этапов.

Задаваясь несколькими значениями давления в напорной линии (например, р_н равно 0,2; 4; 6; 8; 10 МПа) определяем требуемую площадь гидроцилиндра по следующим четырем критериям.

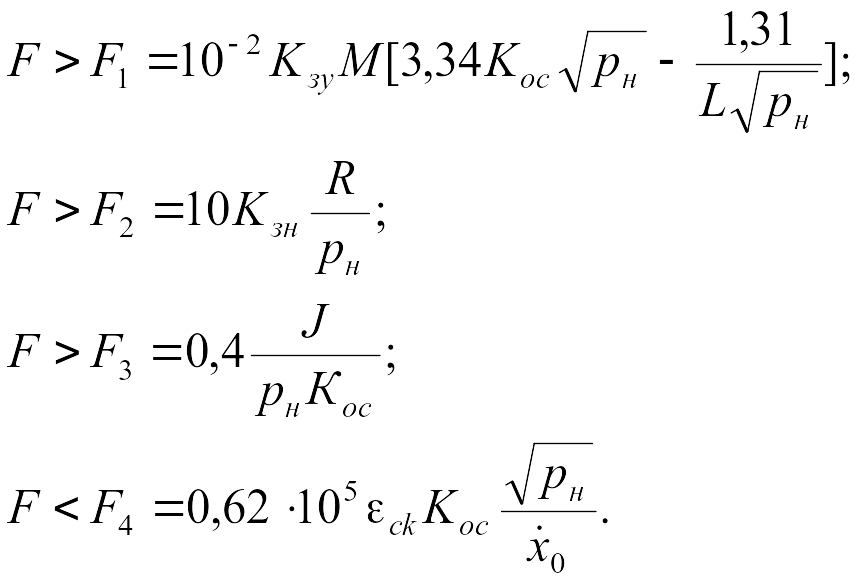(30)

F < F₄ = 0,62 * 10⁵_ск K_ос√p_н/ dx/dt.

1 ‑ уравнение требование устойчивости согласно формуле, К_зу ‑ коэффициент запаса по устойчивости, 2 ‑ требование по полезной нагрузке согласно выражению К_зн ‑ коэффициент запаса по нагрузке, 3 ‑ уравнение требование по жесткости, 4 ‑ требование по скоростной ошибке.

Здесь где F ‑ в см², М ‑ в кг, L ‑ в м, р_н ‑ в МПа, dx/dt ‑ в мм/мин, R ‑ в кН, ε_ск ‑ в мм, J ‑ в Н/мкм.

По результатам расчета в координатах р_н — F строим пересечение областей.

Далее проверяем качество переходного процесса спро­ектированного привода. Если привод окажется излишне задемпфированным (время переходного процесса Т > 0,1 с, перерегули­рование ≈ 1), необходимо увеличить давление или уменьшить площадь в пределах их допустимых значений, если же привод окажется излишне колебательным (Т<0,05 с, перерегулирование >1,3), необходимо уменьшить давление или увеличить площадь.

Если пересечения областей в соответствии с выражениями не существует, необходимо пересмотреть требования к жесткости и скоростной ошибке (уменьшить их).

Для справки: коэффициент вязкого трения λ=1,5∙10⁴ кг/с, объем полости гидроцилиндра , модуль упругости рабочей жидкости E=1,5∙10⁹ Па, передаточное отношение АЗП мм/об, K_y = 0,5∙10^-4  p_н

Исследование работы гдравлического цилиндра в математическом пакете MatLAB

Моделирование можно рассматривать как замещение исследуемого объекта (оригинала) его условным образом, описанием или другим объектом, именуемым моделью и обеспечивающим адекватное с оригиналом поведение в рамках некоторых допущений и приемлемых погрешностей. Моделирование обычно выполняется с целью познания свойств оригинала, путем исследования его модели, а не самого объекта. Разумеется, моделирование оправдано в том случае, когда оно проще создания самого оригинала или когда последний по каким-то причинам лучше вообще не создавать.

Математическое моделирование - это область науки и техники, которая обеспечивает выявление закономерностей протекания различных явлений окружающего нас мира или работы систем и устройств путем их математического описания и моделирования без проведения натурных испытаний. При этом используются фундаментальные положения и законы математики, описывающие моделируемые явления, системы или устройства на некотором уровне их идеализации.

Таким образом, математическая модель системы или устройства это или иное математическое описание их, обеспечивающее имитацию работы систем или устройств на уровне, достаточно близком к реальному поведению их, получаемому при натурных испытаниях систем или устройств.

МАТLАВ, будучи мощной матричной системой, открывает обширные возможности в выполнении численного моделирования как линейных, так и нелинейных систем и устройств, описываемых большими системами уравнений. Такое моделирование предполагает решение системы уравнений состояния достаточно апробированными и хорошо известными численными методами - в том числе на основе рекуррентных и итерационных алгоритмов. Уравнения состояния реальных систем и устройств часто содержат множество нулевых коэффициентов, что порождает разреженные матрицы и массивы. Их аппарат прекрасно представлен в базовой системе МАТLАВ.

Система MATLAB, включая пакет Simulink, образуют мощное средство для проектирования систем автоматического управления (САУ). В теории проектирования САУ важное место уделяется моделированию, анализу и синтезу линейных систем с постоянными параметрами. Для этих целей в системе MATLAB используют пакет Control System Toolbox [13], кроме того, пакет Simulink содержит большой набор средств, который позволяет создавать и анализировать объекты и системы самого различного назначения.

При реализации пакета Control System Toolbox использованы принципы объектно-ориентированного программирования. Введен новый класс объектов: линейные системы с постоянными параметрами (linear time invariant objects, или lti-объекты). Этот класс включает линейные непрерывные или дискретные, одномерные с одним входом и одним выходом (SlSO-системы) и многомерные со многими входами и (или) многими выходами (MIMO-системы). Каждому объекту присваивается определенный идентификатор.

Функции пакета реализуют методы исследования динамических систем, основанные на использовании передаточных функций и моделей для переменных состояния. Частотные и временные характеристики, нули и полюсы систем легко вычисляются и отображаются в виде графиков и диаграмм.

Рабочая среда MATLAB содержит следующие элементы:

• меню;

• панель инструментов;

• окно Workspace, из которого можно получить доступ к содержимому рабочей среды;

• окно Command History, предназначенное для просмотра и повторного вызова ранее введенных команд;

• командное меню Command Window;

• окно Current Folder – браузер файловой системы

Командное меню Command Window – основной элемент среды, позволяющий оперативно решить большинство предложенных в курсе примеров и задач.

Рис. 19. Интерактивная среда моделирования Simulink

Пакет Simulink служит для моделирования различных систем и устройств. Для построения функциональной схемы моделируемых устройств Simulink имеет обширную библиотеку блочных компонентов и удобный редактор блок-схем. Последний основан на использовании возможностей графического интерфейса пользователя и по существу является типичным средством визуального программирования. Используя палитры компонентов (наборы) блок-схем, пользователь с помощью мышки переносит нужные компоненты с палитр на рабочий стол пакета Simulink и соединяет линиями входы и выходы блоков. Таким образом, готовится блок-схема моделирования нужной системы или устройства. Simulink является достаточно самостоятельным инструментом MATLAB и при работе с ним совсем не требуется знать сам MATLAB и остальные его приложения. С другой стороны доступ к функциям MATLAB и другим его инструментам остается открытым и их можно использовать в Simulink. Часть входящих в состав пакетов имеет инструменты, встраиваемые в Simulink (например, LTI-Viewer приложения Control System Toolbox – пакета для разработки систем управления). Запуск Simulink производится из основного окна MATLAB путем нажатия кнопки на панели инструментов

Рис. 20. Запуск Simulink

В левой половине окна браузера приведен перечень библиотек, включенных в состав Simulink, а в правой – перечень разделов соответствующей библиотеки либо изображения блоков соответствующего раздела.

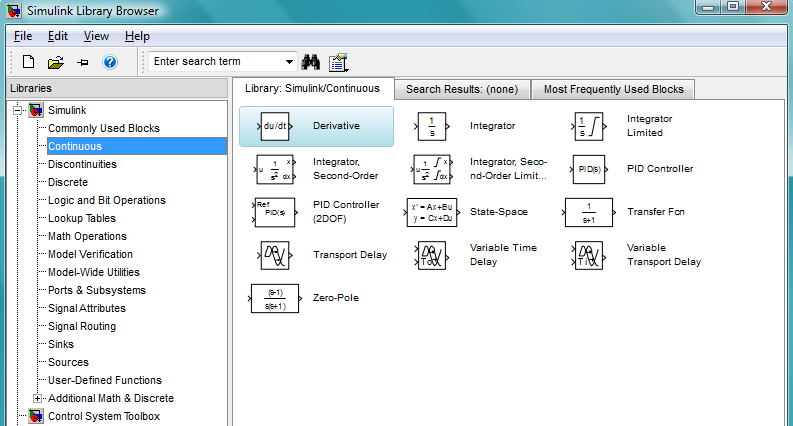
Рис. 21. Браузер библиотек Simulink

Библиотека Simulink содержит следующие основные разделы:

1. Sinks (приемники) – блоки позволяют визуализировать получаемые при моделировании результаты и проконтролировать правильность работы того или иного блока и системы в целом.

2. Sources (источники) – блоки предназначены для формирования сигналов, которые при моделировании обеспечивают работу S-модели в целом или ее частей.

3. Continuous (непрерывные элементы) – содержит блоки, которые реализуют динамические звенья, описываемые линейными дифференциальными уравнениями с постоянными коэффициентами.

4. Discrete (дискретные элементы) – содержит блоки, с помощью которых в модели может быть описано поведение дискретных систем.

5. Math Operations (математические операции) – содержит блоки, которые реализуют некоторые встроенные математические функции системы MATLAB.

Основные блоки раздела Continuous (непрерывные элементы)

1. Integrator – представляет идеальное интегрирующее звено.

2. Derivative – представляет идеальное дифференцирующее звено.

3. State-Space – позволяет задать линейное звено путем ввода четырех матриц его пространства состояний.

4. Transfer Fcn – позволяет задать линейное звено путем ввода его передаточной функции.

5. Zero-Pole – используется для того, чтобы задать звено посредством указания векторов значений его полюсов и нулей, а также значения коэффициента передачи.

6. Transport Delay – обеспечивает задержку сигнала на заданное количество шагов модельного времени.

Чтобы начать сборку блок-схемы моделируемой системы, необходимо вызвать команду File  New  Model.

Сборка блок-схемы S-модели заключается в том, что графические изображения выбранных блоков с помощью мыши перетягиваются из окна раздела библиотеки в окно блок-схемы, а затем выходы одних блоков соединяются с входами других.

Блок-схема моделируемой системы должна включать в себя один или несколько блоков-источников, генерирующих сигналы, которые вызывают «движение» моделируемой системы, и блоки приемников, которые позволяют получить информацию о выходных сигналах этой системы.

Аналогичным образом студенту предлагается самостоятельно оценить частотные свойства системы, воспользовавшись операторами MatLAB nyquist(w) и bode(w). Первый оператор строит частотный годограф Найквиста разомкнутой системы, а второй диаграммы Боде (логарифмическую амплитудно – частотную характеристику и логарифмическую фазо – частотную характеристику). По полученным частотным характеристикам необходимо оценить запас устойчивости ЛЭГП по амплитуде и фазе.

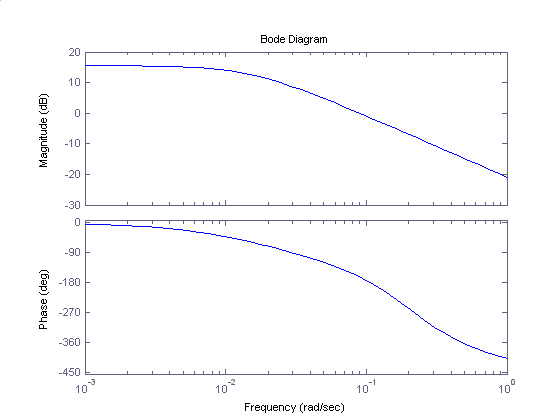
Рис.22. ЛАЧХ и ЛФЧХ

Построим частотный годограф Найквиста (амплитудно-фазовую характеристику) с нанесенной на него координатной сеткой:

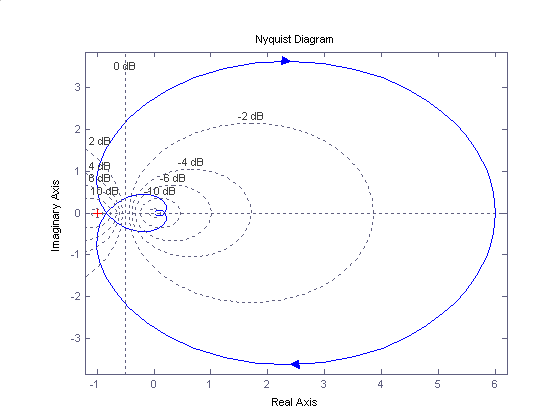
Рис. 23. Амплитудно-фазовая характеристика

Провести анализ устойчивости системы

Определение коэффициентов функции

CurveExpert – программный комплекс, позволяющий быстро находить показатели кривых на графиках. Приложение показывает максимальную зависимость точек. Широкая визуализация помогает наглядно разобраться в постановке системы XY. Удобная вставка позволяет отображать кривые на доступных устройствах. Предустановлены режимы двухмерной системы и опция 3D. Параметрические значения координат устанавливает пользователь, в зависимости от задачи. Возможно сопровождение инфографики пояснительным текстом.

При начале работы с программой необходимо ввести координаты точек, согласно требуемому закону изменения давления. Затем необходимо перейти во вкладку «Tools» и нажать «CurveFinder», необходимо отметить все элементы в этом меню и нажать кнопку «ОК».

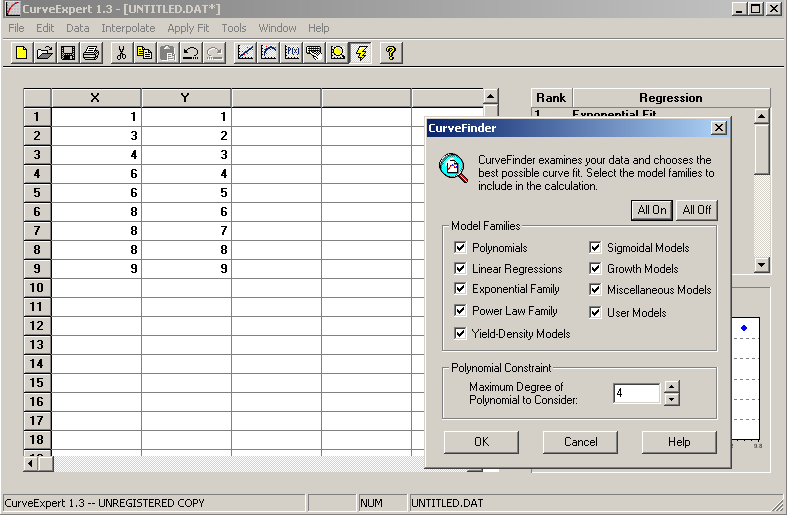
Рис. 24. Интерфейс программы

После появления результатов вычисления, необходимо выбрать функцию, максимально соответствующую введенным данным. Для этого необходимо определить значение «r», которое должно быть максимально близко к единице.

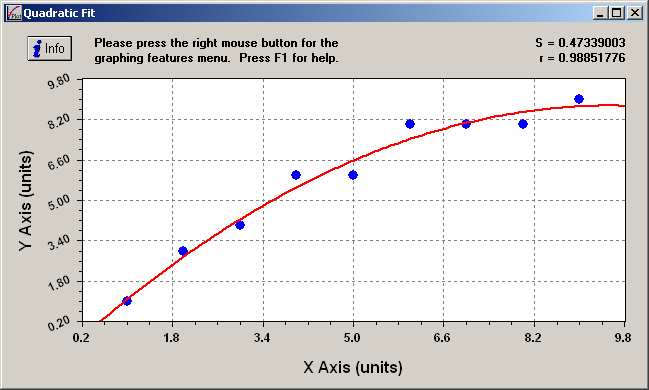
Рис. 15. Определение функции входящего сигнала

При нажатии кнопки «INFO» будет определена функция

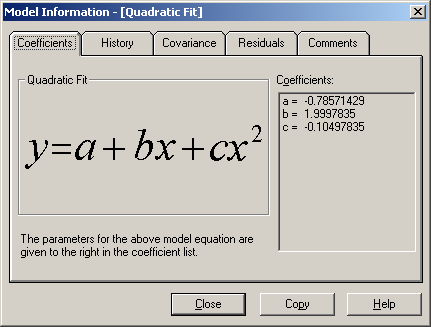
Рис. 26. Определение коэффициентов функции

Для расчета и анализа системы автоматического управления ее передаточная функция должна быть представлена в MatLAB в виде ЛВИ(LTI) – модели (ЛВИ - Линейная Время-Инвариантная). MatLAB обеспечивает возможность построения 4 видов моделей: TF(ПФ - передаточной функции), ZPK(НПК - нули-полюса-коэффициент), SS(ПС- пространство состояния) и FRD(ЗЧО - значения частотного отклика). В данном примере применяются TF- модель.

Для автоматизации расчета площади цилиндра по четырем критериям можно воспользоваться средой программирования системы MatLAB.

Удобным инструментом выбора некоторой из альтернатив будущих вычислений является функция menu MatLAB, которая создает текущее окно меню пользователя. Функция menu имеет следующий формат обращения:

k = menu ('Заголовок меню', 'Альтернатива 1',

'Альтернатива 2', ... , 'Альтернатива n')

Такое обращение приводит к появлению на экране меню. Выполнение программы временно приос­танавливается, и система ожидает выбора одной из кнопок с альтернативами. После правильного ответа выходному параметру k присваивается значение выбранной альтернативы.

Теперь, в зависимости от значения этого параметра, можно по­строить процесс разветвления вычислений. Примерный вид меню для расчета ГП с АРС представлен на рис. 27, а текст scrit-файла на рис. 28.

Рис. 27. Вид меню для расчета ГП

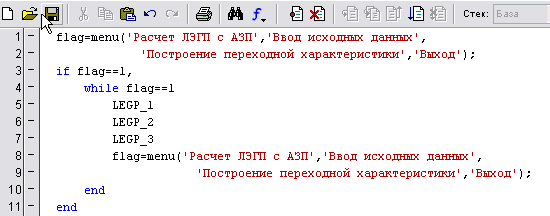
Рис. 28. Текст scrit-файла

Данный скрипт в зависимости от значения переменной flag (1,2, или 3) передает управление файлу legp_1 (Ввод исходных данных), legp_2 (Построение переходной характеристики) или legp_3 (Выход).

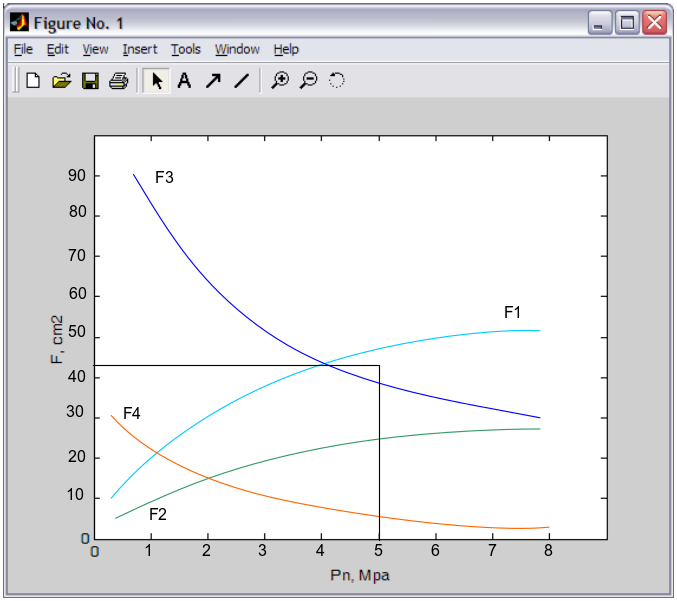
Рис. 29. Окно построения графиков