ВУЗ: Московский технический университет связи и информатики
Категория: Учебное пособие
Дисциплина: Информатика
Добавлен: 15.11.2018
Просмотров: 12820
Скачиваний: 228

121
Аналитический метод поиска минимума применяется только для
ограниченного круга задач. В основном это связано с необходимостью
решения системы нелинейных уравнений, которая, как правило, решается
численными методами. Гораздо проще решать задачу многомерной
оптимизации численными методами, например, такими как метод
градиентного спуска с дроблением шага и методы наискорейшего спуска
с аналитическим или численным выбором шага
.
Вычисление минимума функции нескольких переменных
z = f(x
1
, x
2
, …x
n
)
в Scilab осуществляет той же функцией optim(), что и для функции от одной
переменной, но в назначении параметров имеются некоторые отличия.
Общий формат функции optim() следующий:
[f,xopt]=optim(costf,x0)
,
где входными параметрами в случае в случае решения задачи многомерной
оптимизации являются:
x0- вектор-столбец начальных приближений длиной n (n – количество
параметров оптимизации);
constf– имя функции, для которой ищется минимум.
Функция возвращает значения параметров:
f - минимальное значение функции и xopt - значения параметров
оптимизации, при которых функция достигает минимального значения.
Функция optim() требует вспомогательную функцию costf(), имеющую
следующую структуру:
function [f,g,ind]=costf(x,ind)
f=gg(x);
g=numderivative(gg,x);
endfunction
где f - функция, минимум которой ищется;
g - градиент функции f (вектор частных производных f по x).
ind- является внутренним параметром для связи между optim и costf.
Используя функцию optim() необходимо помнить, что параметр ind должен
быть определен в функции costf. Подробности об этом параметре описаны в
2.5.1.
2
1
2
2
2
2
2
2
2
2
Q
0,
x
Q
Q
Q
0.
x
y
x y
122
Таким образом, решение задачи оптимизации в пакете Scilab
требует дополнить функцию optim() функцией costf, которая возвращает
значение минимизируемой функцию f и ее частных производных.
Чтобы с использованием optim() вычислить локальный максимум
необходимо взять целевую функцию с противоположным знаком.
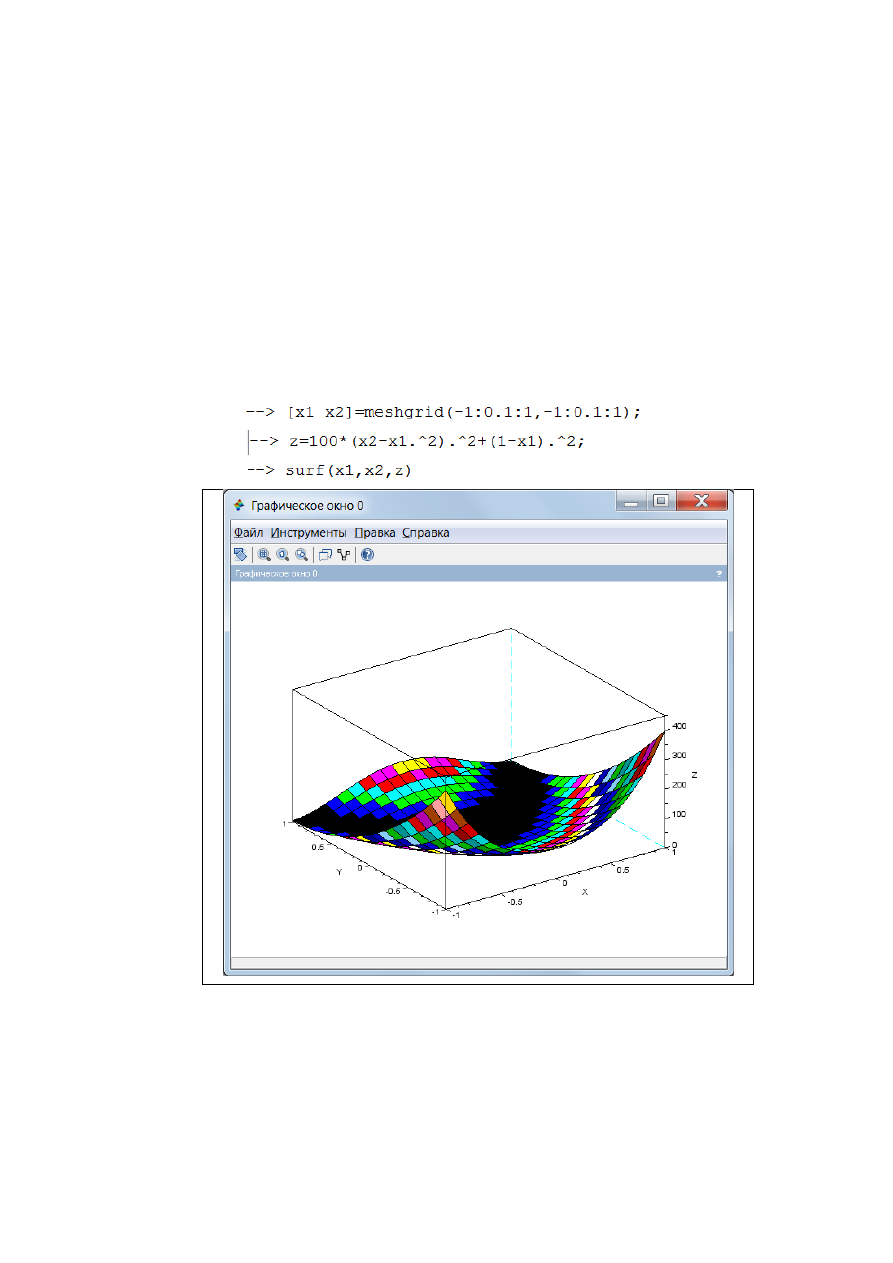
Рассмотрим работу функции optim() на примере определения
минимума двумерной функцииf(x
1
, x
2
) = 100(x
2
–x
1
2
)
2
+(1-x
1
)
2
.
Построим график (рис. 2.6.1-1) с использованием функции ezsurf(),
аргументами которой служат: выражение функции, заключенное в
одинарные кавычки, вектор изменения первой производной и вектор
изменения второй переменной.
Рис. 2.6.1-1. Результат выполнения функции surf()
Определим координаты точки минимума и значение функции в этой
точке с использованием функции Scilab optim()(рис.2.6.1-2).

123
Рис. 2.6.1-3.Использование функции optim() для нахождения
минимума многомерной функции

124
2.6.2. Лабораторная работа по теме
«Технология решения задач многомерной оптимизации»
1. Вопросы, подлежащие изучению
1) Построение графиков функции от двух переменных F(x
1
,х
2
)средствами
пакета Scilab.
2) Нахождение
координат точки минимум функции F(x
1
,х
2
)
с
использованием встроенных функций пакета Scilab - optim().
2. Общее задание
1) Изучите материалТемы 2.6 (п. 2.6.1).
2) Выберите индивидуальное задание из табл. 2.6.2-1.
3) Постройте график функции F(x
1
,х
2
);
4) Сформируйте для использования функции optim() вспомогательную
функцию, необходимую для вычисления функции и частных
производных.
5) Найдите
координаты
точки
минимум
функции
F(x
1
,х
2
)с
использованием встроенной функций optim();
6) Получите
значение
функции,
значений
ее
параметров,
обеспечивающих оптимальное значение и частных производных в
точке минимума.
7) Сохраните текст рабочего окна на внешнем носителе.
8) Предоставьте результаты работы преподавателю, ответить на
поставленные вопросы.
9) Выполните команду clearall.
10)
Оформить отчет по выполненной работе.
1. Варианты индивидуальных заданий
Таблицы 2.6.2-1
№
Функции для вычисления минимума
1
22
2
3
5
2
)
,
(
1
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
F
2
2
1
2
1
2
2
2
1
2
1
2
2
)
,
(
x
x
x
x
x
x
x
x
F
3
13
3
5
3
)
,
(
1
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
F
4
2
2
1
2
2
2
1
2
1
2
)
,
(
x
x
x
x
x
x
x
F
5
18
2
4
3
5
)
,
(
1
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
F

125
6
10
3
3
2
)
,
(
2
1
2
2
2
1
2
1
x
x
x
x
x
x
F
7
21
2
2
5
)
,
(
2
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
F
8
3
2
3
2
)
,
(
1
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
F
9
10
2
5
)
,
(
2
1
2
2
2
2
2
1
2
1
x
x
x
x
x
x
x
F
10
8
3
3
4
)
,
(
2
2
2
2
1
2
1
x
x
x
x
x
F
11
5
2
6
3
)
,
(
1
2
2
2
1
2
1
x
x
x
x
x
F
12
16
2
)
,
(
2
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
F
13
16
2
)
,
(
2
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
F
14
11
2
4
)
,
(
2
1
2
2
2
1
2
1
x
x
x
x
x
x
F
15
1
2
1
2
2
2
1
2
1
2
2
)
,
(
x
x
x
x
x
x
x
F
16
4
2
2
)
,
(
2
1
2
2
2
1
2
1
x
x
x
x
x
x
F
17
15
3
2
3
)
,
(
2
1
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
x
F
18
12
2
2
)
,
(
1
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
F
19
18
5
2
)
,
(
1
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
F
20
9
2
2
3
)
,
(
2
1
2
2
2
1
2
1
x
x
x
x
x
x
F
21
2
1
2
1
2
2
2
1
2
1
2
2
)
,
(
x
x
x
x
x
x
x
x
F
22
26
3
2
)
,
(
2
1
2
2
2
1
2
1
x
x
x
x
x
x
F
23
13
3
5
)
,
(
2
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
F
24
11
2
3
4
)
,
(
1
2
2
2
1
2
1
x
x
x
x
x
F
25
2
1
2
2
2
1
2
1
2
6
3
)
,
(
x
x
x
x
x
x
F
26
4
2
2
)
,
(
2
1
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
x
F
27
12
3
2
3
)
,
(
2
1
2
2
2
1
2
1
x
x
x
x
x
x
F
28
12
2
4
)
,
(
1
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
F
29
16
2
5
)
,
(
1
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
F
30
9
2
2
3
)
,
(
2
1
2
1
2
2
2
1
2
1
x
x
x
x
x
x
x
x
F
2. Содержание отчета
1) В форме комментариев:
• Название лабораторной работы
• ФИО студента, номер группы
• № варианта
• Индивидуальное задание