Файл: Электронное пособие Scilab.pdf

116 

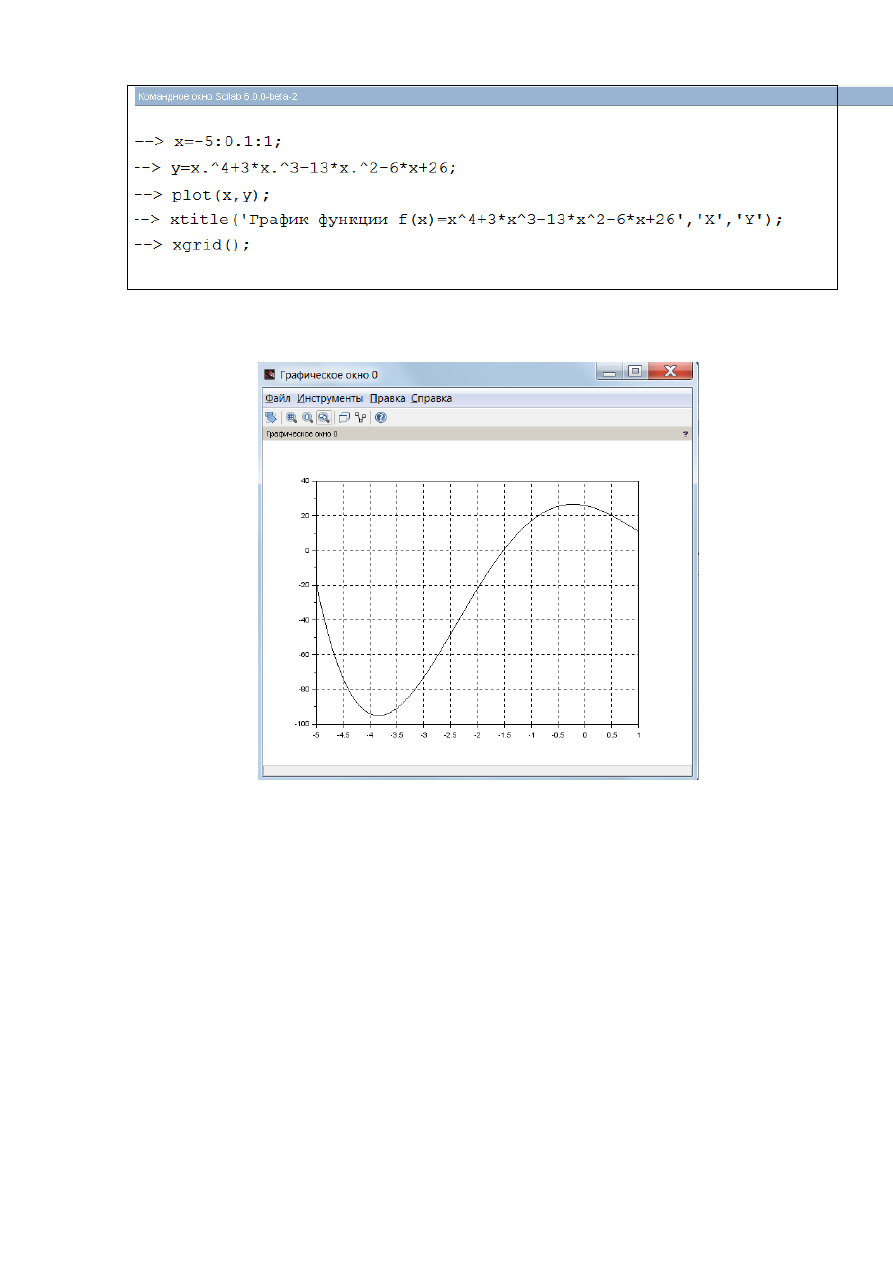
Рис. 2.5.1-1. Построение графика функции f(x) 

Рис. 2.5.9-2. График функции f(x) 

 
Из графика следует, что на отрезке[-4;-2] имеется локальный минимум. 

Исследуем функцию и поведение производных. 

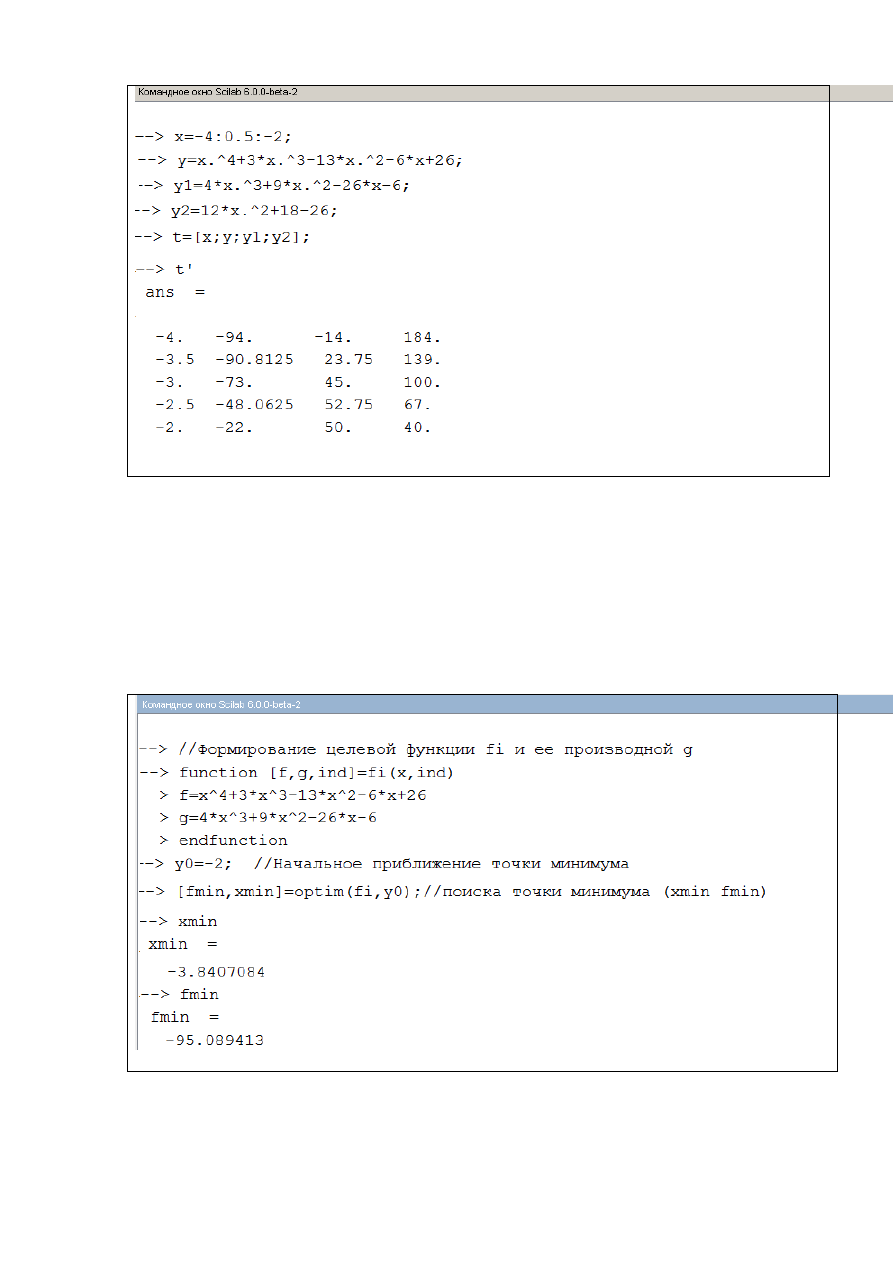
Получение  значений  функции  и  производных  на  выбранном  отрезке 

приведено на рис. 2.5.1-3. 

117 

Рис.2.4.1-3. Исследование функции f(x) на отрезке [-4;-2] 

Из полученной таблицы значений функции и производных видно, что 

на  отрезке  [-4;-2]  существует  единственный  минимум.  Найдем  координаты 
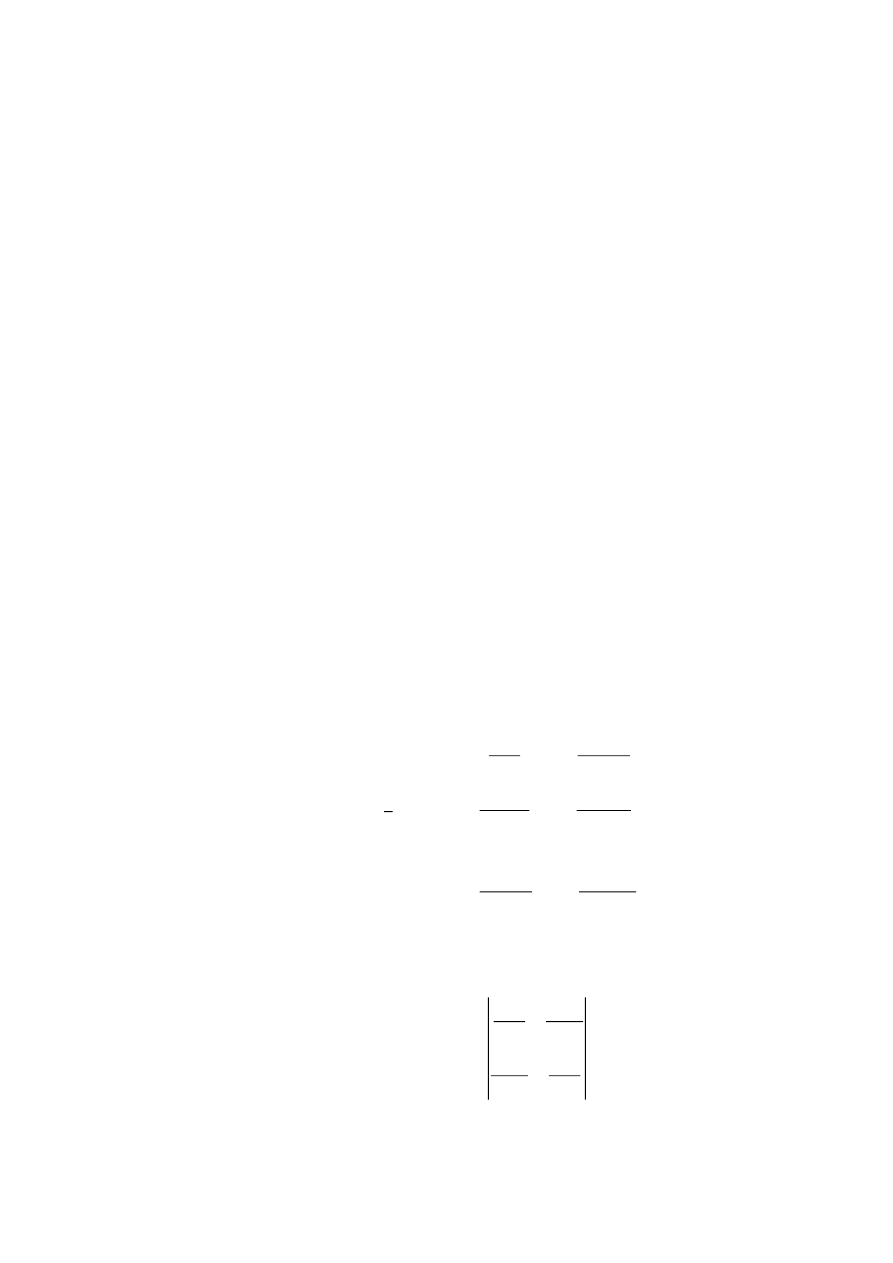
этого минимума с использованием функции Scilab optim() (рис. 2.5.1-4). 

Если  для  целевой  функции  затруднительно  находить  производные,  то 

для того чтобы найти границы унимодальности функции можно построить ее 
график и выбрать отрезок, содержащий единственный минимум. 

Рис.2.4.1-4. Нахождение координат точки минимума функции f(x) 

118 

2.5.2. Лабораторная работа по теме 

«Технология решения задач одномернойоптимизации» 

1. Вопросы, подлежащие изучению 

 
1)  Условие унимодальности функции на отрезке. 
2)  Получение  таблиц  значений  функции  и  ее  производных  с 

использованием средств пакета Scilab. 

3)  Технология  использования  встроенной  функции  пакета  Scilab  – 

optim(). 

2. Общее задание 

1)  Изучите материал Темы 2.5 (п. 2.5.1). 
2)  Выберите индивидуальное задание из табл. 2.5.2-1. 
3)  Построите  график  функции  f(x),  выбрать  отрезок,  содержащий 

минимум; 

4)  Проверьте  на  выбранном  отрезке  условие  унимодальности  функции, 

получив таблицу значений первой или второй производной. 

5)  Создать  функцию  для  формирования  значений  целевой  функции  и  ее 

производной. 

6)  Найдите  координаты  точки  минимума  f(x)  с  использованием 

встроенной функции Scilab optim(). 

7)  Сохраните текст рабочего окна на внешнем носителе. 
8)  Предоставьте  результаты  работы  преподавателю,  ответьте  на 

поставленные вопросы. 

9)  Выполните команду clear all. 
10)  Оформите отчет по выполненной работе. 

3. Варианты индивидуальных заданий 

Таблица 2.5.2-1 

№ 

f(x) 

№ 

f(x) 

1 

????

2

− 6 ln(???? + 1) + 2,8 

16 

2????

2

− sin ???? − 1,5 

2 

????

2

− 4 sin ???? + 0,8 

17 

2 cos(???? − ????

3

) − ???? 

3 

????

2

− 3 sin ???? − 2,4 

18 

????

2

− 3,4 ln(1 + ????) − 1 

4 

????

2

+ sin ???? − 0,5√(1 + 2????)

3

19 

e

x

− (x + 1)

2

− 2 

5 

3????

2

− 2 cos(???? + 1) − 4,8 

20 

????

2

− sin ???? 

119 

6 

????

2

− 1,5 cos(???? + 3) − 1,8 

21 

e

x

− 4x − 9,5 

7 

ln(???? + 2) + cos(2 + ????)

− 0,35 

22 

????

2

− 3sin ???? − 2???? 

8 

????

3

− 4,8 sin(1 + 2????) − 1 

23 

3 − 2 sin ???? − √????

2

+ 1 

9 

????

2

− 2 sin(???? + 1) − 2 

24 

−(2 + 3 sin ???? − √????

2

+ 2 

10 

????

????−3

− ln(???? + 3) + 1 

25 

e

−0,4x

+ 3x

2

− 5x − 3 

11 

− sin ???? − √???? + 1 

26 

????

2

+ cos(???? − 4)

+ √???? + 1 − 3 

12 

cos(???? − 0,2????

2

) − ???? + 6 

27 

????

2

− ln ???? − 3 

13 

e

x

− 4x 

28 

−???? + ????

0,5????

14 

0,1????

2

+ ???? ln ???? − ???? + 0,5 

29 

− sin ???? − √1 + ???? + 2 

15 

2e

−x

+ e

x

− 4 

30 

4x

3

+ 2x

4

+ 9,5e

−2x

− 35 

1.  Содержание отчета 

1)  В форме комментариев: 

•  Название лабораторной работы 
•  ФИО студента, номер группы 

•  № варианта  
•  Индивидуальное задание 

2)  Протокол вычислений (сессии) в Командном окне.  

2.5.3. Контрольные вопросы по теме 

1)  Понятия локального и глобального минимума функции? 
2)  Можно ли средствами Scilab вычислить глобальный минимум 

заданной функции? 

3)  Какие исследования функции необходимо произвести перед 

применением перед поиском локального минимума? 

4)  Функция optim() и назначение ее входных и выходных параметров. 
5)  Для чего при использовании функции optim() необходимо 

сформирование вспомогательной функции? 

6)  Можно ли с использованием функции вычислить локальный 

максимум? 

120 

Тема 2.6. Технология решения задач многомерной 

оптимизации  

2.6.1. Решение задач многомерной оптимизации функций 

2.6.2.  Лабораторная работа  
2.6.3. Контрольные вопросы по теме 

2.6.1.  Решение  задач многомерной оптимизации 

Задача,  требующая  нахождения  оптимального  значения  функции  m 

переменных  Q(Х)=Q(x

1

,  x

2

,  …,  x

m

),  называется  задачей  многомерной 

оптимизации.  Так  же,  как  и  для  случая  одномерной  оптимизации,  задача 
нахождения  максимума  функции  сводится  к  задаче  нахождения  минимума 
путем замены целевой функции Qна  -Q. 

В постановке задачи безусловной оптимизации для  Q(Х)=Q(x

1

,  x

2

, …, 

x

m

) требуется найти хотя бы одну точку минимума Х* и вычислить Q*=f(Х*). 

Точка  Х*R

m

  называется  точкой  глобального  минимума  функции  Qна 

множестве Х, если для всех ХR

m

 выполняется неравенство Q(Х*) Q(Х). В 

этом  случае  значение  Q(Х*)  называется  минимальным  значением  функции 
Qна R

m

. Точка Х*R

m

 называется точкой локального минимума функции Q, 

если  существует  такая    -  окрестность  U



этой  точки  (>0),  что  для  всех 

ХХ



=Х



U



 выполняется неравенство Q(X*)Q(X). 

Для  всякой  непрерывно  дифференцируемой  функции  Q  достаточным 

условием  того,  функция  имеет  точку  минимума,  является  положительная 
определенность матрицы вторых частных производных (матрицы Гессе): 

Известно, что, для того чтобы матрица была положительно определена, 

необходимо,  чтобы  все  угловые  миноры  были  положительны.  Так  для 
функции двух переменных Q(x, y) матрица Гессе имеет вид: 

, 

а достаточное условие существования минимума является выполнение 

неравенств: 

2

2

2

1

1

m

2

2

2

1

2

m

2

2

m

1

m

m

f

f

...

x

x x

f

f

...

G(x)

f (x)

x x

x x

...

...

...

f

f

...

x

x

x

x















 





















  

 

























 

 





2

2

2

2

2

2

Q

Q

x

x y

G(x, y)

Q

Q

y x

y







 







 

