Добавлен: 19.10.2018
Просмотров: 3283
Скачиваний: 7

уравнения f(x) = 0 построить график функции y =f(x) и найти точки пересечения
кривой с осью абсцисс, в которых эта функция равна нулю. Наконец, корень
уравнения можно попытаться определить "методом подбора".
Однако ни один из перечисленных подходов нельзя считать достаточно
эффективным при решении инженерных и научных задач на ЭВМ. Более
предпочтительны способы, обеспечивающие одновременно как оператив-
ность получения результата, так и высокую точность.
Второе важное требование к методу - универсальность, то есть спо-
собность находить решения для разных видов уравнений. В особенности эти
требования должны соблюдаться в специальных пакетах программ, предна-
значенных для выполнения большого объема расчетов, например, в системах
автоматизированного проектирования (САПР).
В связи с этим для решения нелинейных уравнений на ЭВМ широко при-
меняются специальные методы, которые относятся к методам вычислительной
математики. На их основе создано большое число алгоритмов, различающихся
сложностью и эффективностью.
Когда говорят о методах решения нелинейных уравнений на ЭВМ, то
подразумевают в первую очередь итерационные методы. Главным признаком
итерационного метода является многократное повторение одного и того же
набора действий для получения результата (в переводе с англ. iteration -
повторение).
В основе итерационного метода лежит итерационная, то есть повто-
ряемая процедура. Процедура эта строится таким образом, что после каждого ее
выполнения производится очередное приближение к корню. Можно сказать,
что итерационный метод несколько напоминает отыскание корня подбором,
однако этот подбор производится не "наугад", а по вполне определенному алго-
ритму. Основные особенности итерационных методов будут рассмотрены поз-
же - при описании самих методов.
1.2. Исследование уравнений и отделение корней
Каждый, кто пытался найти корень уравнения подбором, знает, на-
сколько важен выбор первого пробного значения неизвестного x. Точно так
же при поиске корня итерационным методом, необходимо правильно опре-
делить начальное значение x. От этого иногда зависит не только скорость ре-
шения задачи, но и вообще возможность получения результата. Рассмотрим
способы исследования уравнений для предварительной оценки корней.
1.2.1. Исследование уравнения и отделение корней
При решении практических задач обычно приходится проводить пред-
варительное исследование уравнения до его решения. Дело в том, что если
уравнение не удается решить аналитически, то заранее трудно определить,
сколько оно имеет корней и какова их природа - сколько из них комплексных
или вещественных, сколько отрицательных или положительных. Поиск корней

"наугад" без предварительного исследования чреват тем, что правильный ответ
так и не будет найден. Кроме того, зачастую некоторые корни не имеют физи-
ческого смысла, и поэтому нет необходимости определять их точные значения.
Например, поведение резонансной электрической или механической сис-
темы обычно описывается так называемым характеристическим уравнением,
корни которого соответствуют значениям ее собственных частот. Сложные
объекты, как правило, имеют множество собственных частот, что усложняет
анализ. Однако в ходе предварительного исследования уравнения можно, не
вычисляя точных значений всех корней, сразу выбрать из них те, которые
представляют наибольший интерес.
1.2.2. Графическое исследование уравнения
Как было указано в п. 1.1, примерное положение корней уравнения
f(x) = 0 на числовой оси легко определить, построив график функции у
=f(x). Точки пересечения кривой y =f(x) с осью абсцисс, где y = 0, и будут соот-
ветствовать искомым корням.
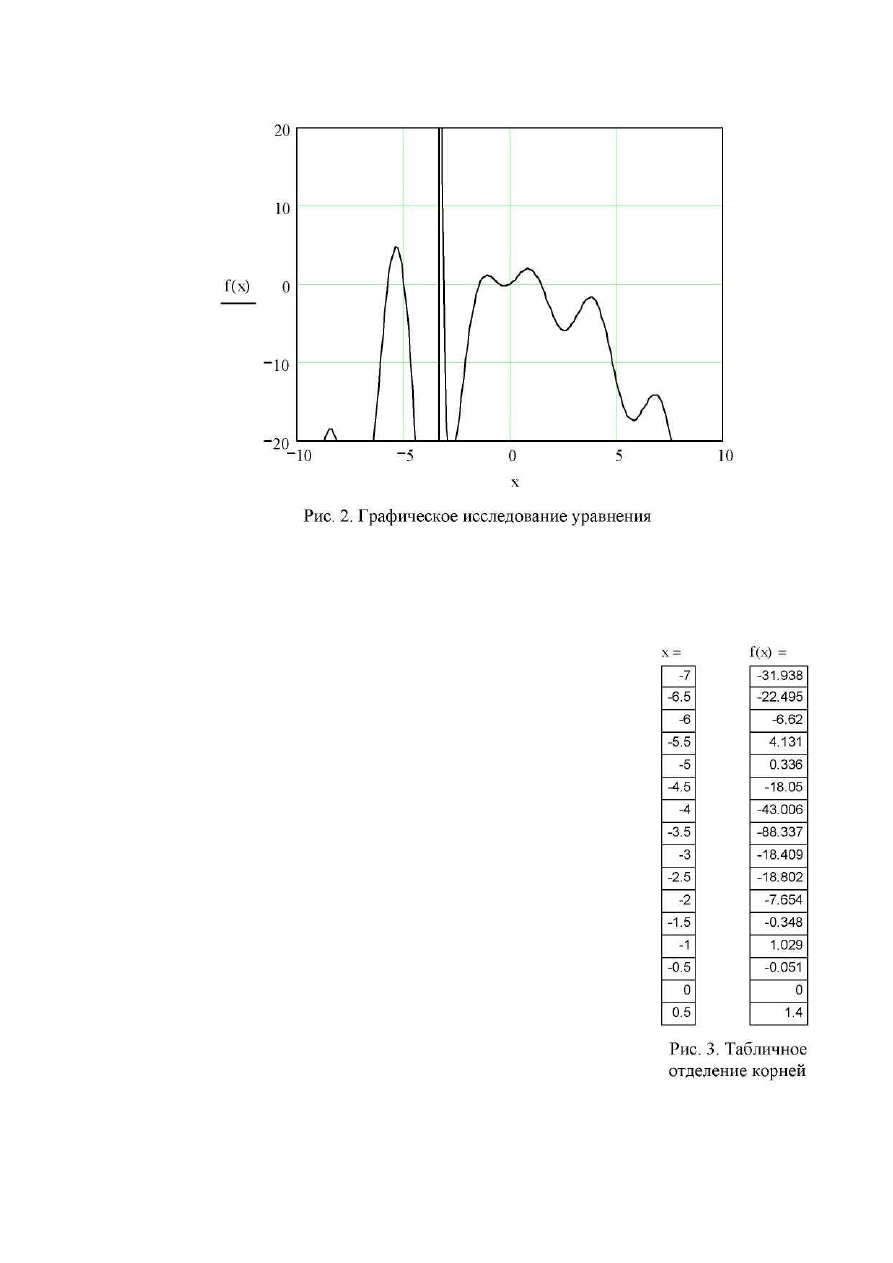
В качестве примера на рис. 2 представлен график, построенный в пакете
MathCAD для уравнения (3) - см. п. 1.1. Из рисунка видно, что уравнение имеет
семь действительных корней в интервале примерно от -7 до +2: пять отрица-
тельных, один при нулевом значении x и один положительный. В точке x ≈-3,3
функцияf(x) имеет разрыв.
Приведенный график позволяет провести отделение указанных корней, то
есть найти на оси x границы отрезков, в каждом из которых располагается не
более одного корня.
х:=-10,-9.9.. 10
2
4
,
0
1
3
,
0
1
1
,
2
)
2
sin(
:
)
(
x
x
x
x
x
f
Проведите исследование уравнения (4) самостоятельно. 1.2.3.
Табличный способ отделения корней
Отделение корней также нередко выполняют с по-
мощью табличного представления зависимости f(x). Для
этого формируют таблицу, в которую заносят ряд по-
следовательно расположенных на оси x точек xi и
вычисленные в них значения левой части уравнения
f(x
i
).
Затем в таблице выбирают те пары рядом распо-
ложенных точек, между которыми функция f(x) меняет
свой знак. При этом для обнаружения корня по сути де-
ла используется тот же признак, что и при графическом
исследовании - изменение знака функции.
На рис. 3. представлены полученные с помощью
пакета MathCAD результаты расчета зависимости f(x) в
виде таблицы при постоянном шаге изменения аргу-
мента Δх = x
i+1
- x
i
. Расчет выполнен для того же транс-
цендентного уравнения, что и на рис. 2.
Приведенные данные показывают, что первый из корней уравнения
f(x) = 0 лежит в пределах -6 < x < -5,5, поскольку значенияf(x) в точках х
= -6 и x = -5,5 имеют разные знаки.
С целью облегчения поиска корней процедуру вычисления нередко
оформляют в виде программы на ЭВМ, включая в ее алгоритм не только вы-

числение значений x
i
и f(x
i
), но и автоматическое выявление тех отрезков, в ко-
торых предположительно должны находятся корни уравнения.
Однако пользоваться подобными процедурами автоматического отде-
ления корней следует осторожно. Дело в том, что смена знака функции на неко-
тором отрезке x
i
≤х ≤x
i+1
не является надежным признаком существования корня.
Во-первых,f(x) может изменить свой знак в точке разрыва, как это про-
исходит в точке x ≈-3,3 на рис. 2. Во-вторых, даже если функция f(x) непре-
рывна, изменение ее знака на рассматриваемом отрезке может быть обусловлено
не одним, а несколькими корнями, например, тремя или пятью. И, наоборот,
совпадение знаков функции f(x) на краях отрезка не является доказательством
отсутствия корней. К примеру, в случае двух корней на отрезке функция дваж-
ды переходит через точки y = 0 и дважды меняет свой знак на обратный. Или
имеется так называемый кратный корень, когда f(x) не пересекает, а только ка-
сается оси x в некоторой точке.
Из вышесказанного следует, что табличное отделение корней жела-
тельно проводить, выбирая как можно более малый шаг изменения аргумента, и
сопровождать его графическим исследованием.
1.3. Методы поиска корней уравнения
Рассмотренные способы исследования позволяют уточнить количество
корней уравнения, их свойства и примерное положение на числовой оси. После
отделения корней определить их значения с требуемой точностью можно с по-
мощью методов, описание которых дано ниже.
1.3.1. Модификация табличного способа
Несложную итерационную процедуру для отыскания приближенного ре-
шения уравнения можно построить на основе рассмотренного выше табличного
способа отделения корней. Рассмотрим ее.
Предположим, в результате предварительного исследования определен
отрезок [a, b], содержащий только один корень уравнения f(x) = 0. Разобьем
этот отрезок на некоторое количество равных частей. Для этого возьмем, к
примеру, N - 1 = 99 точек, расположенных с постоянным шагом Δх
= ( b - a ) / 100 на [a, b] и разделим его таким образом на N = 100 частей. Вычис-
лим в этих точках значения функции f(x). Из полученных ста новых отрезков
выберем тот, в котором находится корень. Его легко определить по перемене
знака f(x) при переходе от одной точки к другой.
Для дальнейшего уточнения положения корня на числовой оси описанные
действия можно повторять многократно, построив, таким образом, на их основе
итерационную процедуру. Действительно, на первом итерационном шаге отре-
зок, в котором заключен корень, уменьшается в N = 100 раз. Уменьшив на
втором шаге отрезок еще в сто раз, получим сокращение длины уже в N х N =
10000 раз при суммарном количестве расчетных то чек N N + = 1 98.
На третьем шаге общее сокращение достигнет 100 х 100 х 100 =
1000000 раз, а количество расчетных точек возрастет до N+ N+ N = 297.
Общий же коэффициент сужения на K-м шаге составит N
K
.
Процедуру сжатия отрезка, содержащего корень, следует остановить, ес-

ли на очередном шаге будет получено значение f(x) достаточно близкое к нулю.
Последнее означает, что найдено приближенное решение уравнения, соответст-
вующее f(x) ≈ 0. Условие прекращения итерационной процедуры обычно запи-
сывают в виде
| f (x) | ≤ δ, (5)
где δ - некоторое малое положительное число. При выборе δ руководствуются
требованиями к точности решения уравнения и порядком величины f(x).
1.3.2. Метод половинного деления
Другие названия: метод бисекции, метод дихотомии (от греч. Six-
oc - на две части и
IOJUT
)
- сечение).
Метод половинного деления можно рассматривать как дальнейшее усо-
вершенствование описанной выше процедуры поиска корня уравнения. Отли-
чие метода половинного деления состоит в том, что отрезок на каждом шаге
разбивается не на любое произвольное число частей N, а делится только на две
части, то есть N=2.
Графически процедура поиска корня уравнения f(x) методом половинного
деления показана на рис. 4.