Добавлен: 19.10.2018
Просмотров: 3287
Скачиваний: 7

Задание 8. В гибридных интегральных схемах в
качестве одновитковой индуктивности может приме-
няться тонкая металлическая полоска, нанесенная
на диэлектрическую подложку в виде круглой петли
( с м . р и с у н о к ) . И н д у к т и в н о с т ь т а к о й п е т л и
в наногенри приближенно определяется по
формуле
где R - радиус средней линии петли, W - ширина металлической полоски,
t - ее толщина. Все размеры в формуле указаны в миллиметрах.
Найдите размер R, удовлетворяющий требуемому значению L при
заданных параметрах Wиt (их значения указаны в таблице).
Задание 9. Для экспериментально полученной прямой ветви вольт-
амперной характеристики полупроводникового диода при u < 0,6 В подобра-
на аппроксимация в виде степенного многочлена:
i = au + bu
2
+ cu
3
+du
4
+eu
5
,
где ток i задан в миллиамперах, напряжение u - в вольтах.
Используя аппроксимацию, найдите напряжение на
диоде, при котором через него будет протекать заданный в таблице ток i.
При составлении уравнения используйте указанные в таблице параметры
a, b, c, d и e.
2
8
ln
257
,
1
t
W
R
R
L
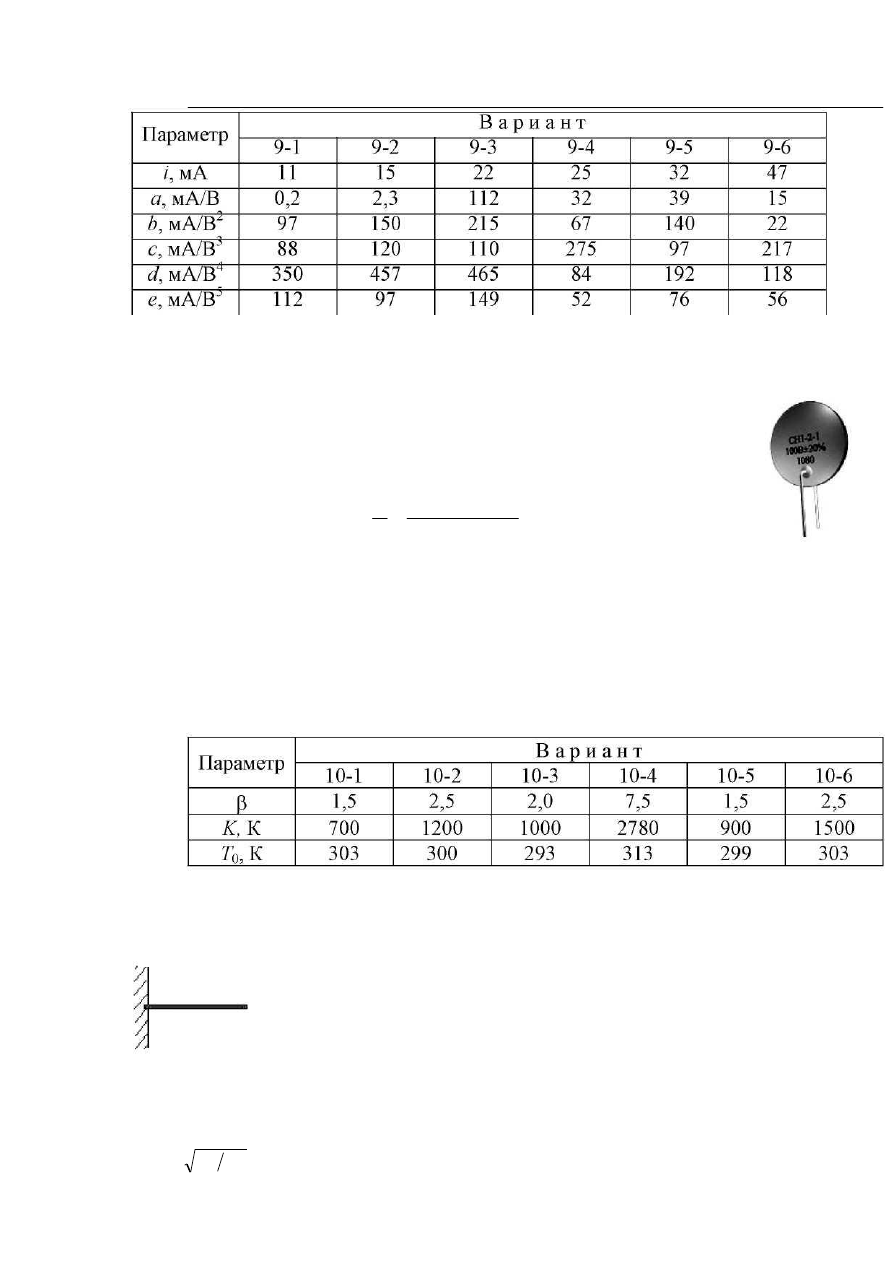
Задание 10. Коэффициент нелинейности полупроводникового
нелинейного резистора (варистора) Р определяется как отношение ста-
тического R и дифференциального r сопротивлений. При за-
данном постоянном напряжении зависимость Р от температуры
описывается выражением
где Т - температура активной области варистора, Т
0
- температура ок-
ружающей среды, K - коэффициент температурной чувствительности
рабочего слоя варистора.
Найдите значение Т, при котором обеспечивается заданное зна-
чение Р для известных K и Т
0
.
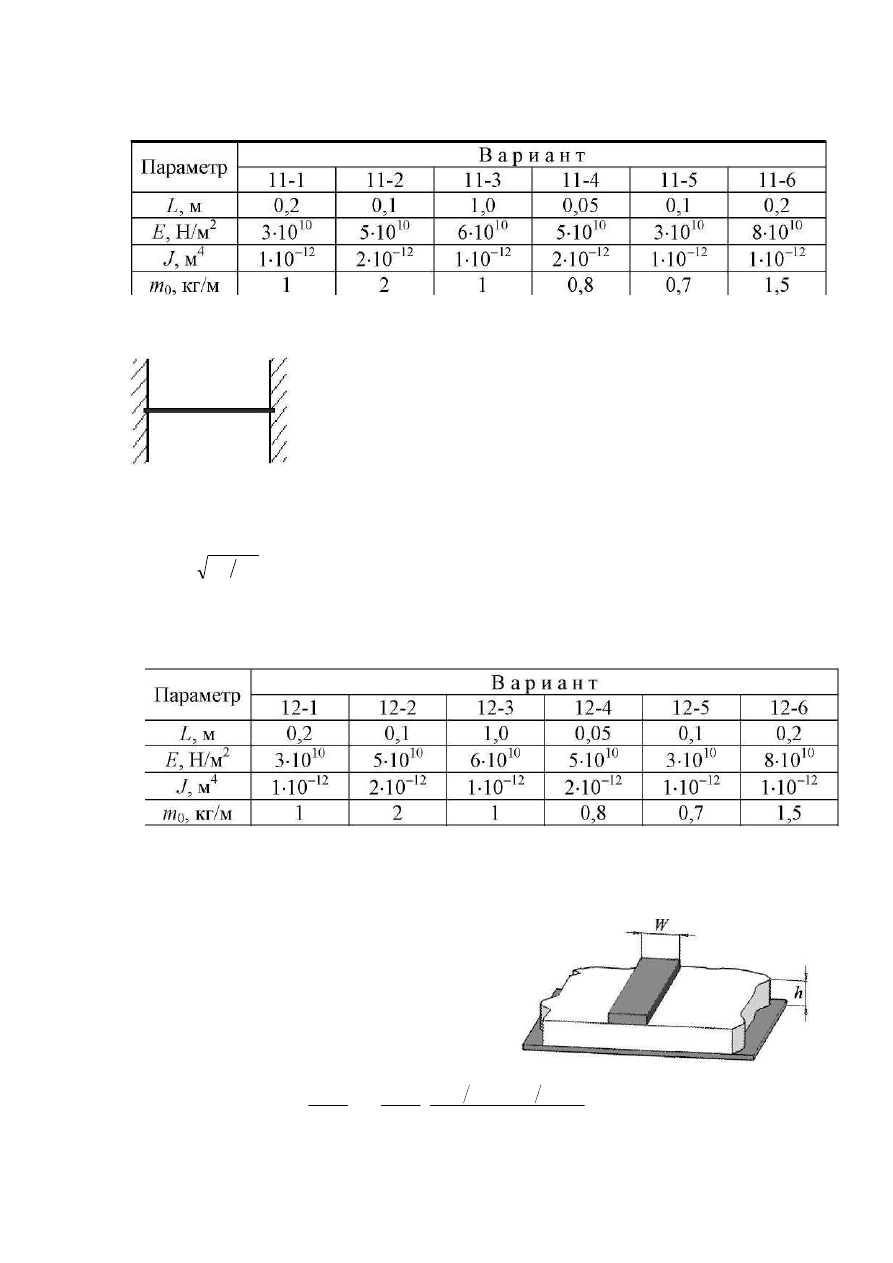
Задание 11. Конструкция радиоэлектронного устройства содержит кон-
сольный тонкий однородный стержень. Частоты механиче-
ских резонансов стержня при таком закреплении определя-
ются из уравнения
cos(x) ch(x) + 1 = 0 ,
где x = kL - безразмерный параметр, k - волновое число, L - длина стержня.
Собственная частота стержня со связана с параметром k соотношением
0
2
m
EJ
k
, где E - модуль упругости материала, J - момент инерции
сечения, M
0
-
погонная масса стержня.
Найдите первые пять резонансных частот стержня при заданных в таб-
0
2
0
2
KT
KT
T
KT
KT
T
r
R
лице исходных данных.
Задание 12. Конструкция электронного устройства содержит тонкий
однородный стержень, жестко закрепленный на концах.
Частоты механических резонансов стержня при таком за-
креплении определяются из уравнения
cos(x) ch(x) - 1 = 0 ,
где x = kL - безразмерный параметр, k - волновое число,
L - длина стержня. Собственная частота стержня со связана с парамет-
ром k соотношением
0
2
m
EJ
k
где E - модуль упругости материала,
J- момент инерции сечения, m
0
- погонная масса стержня.
Найдите первые пять резонансных частот стержня при заданных в
таблице исходных данных.
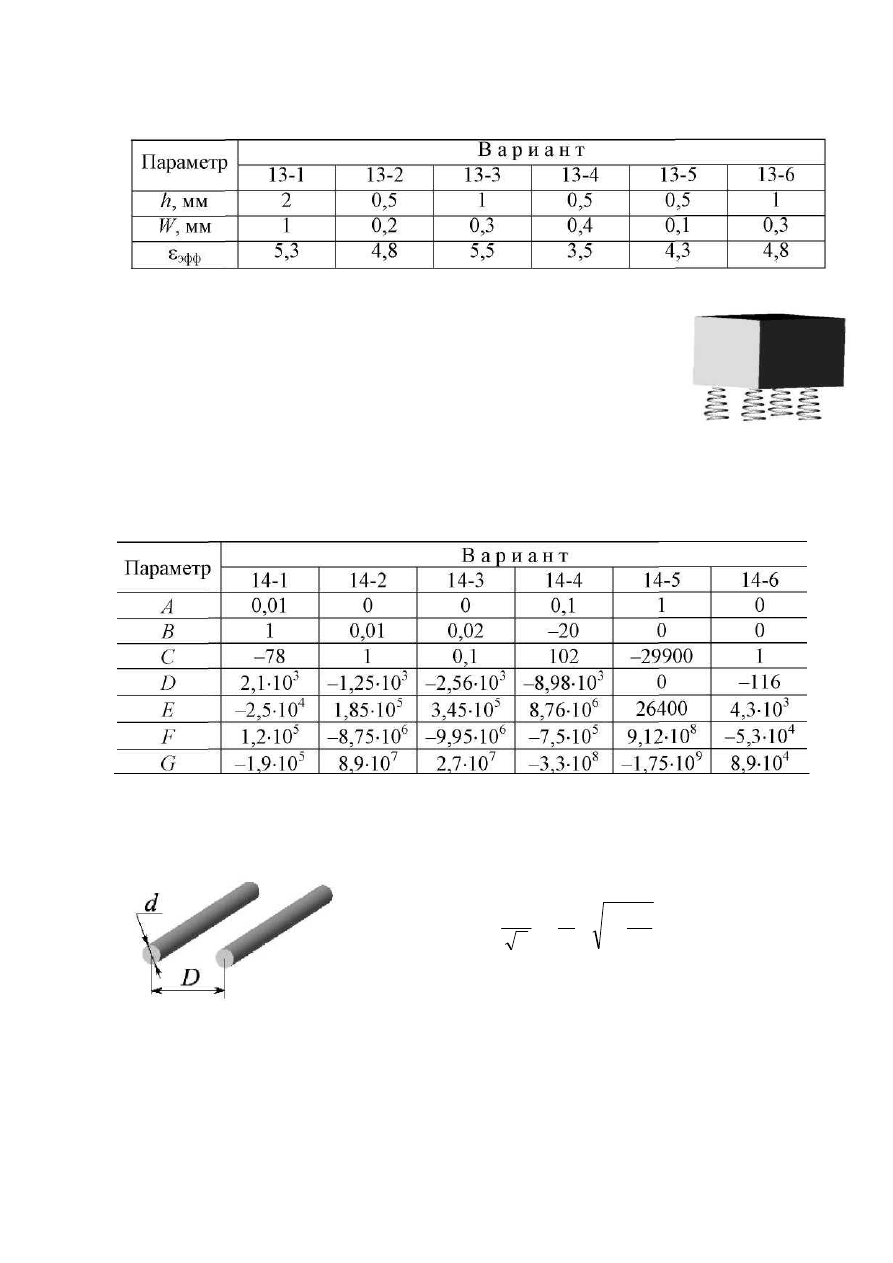
Задание 13. Линии связи в высокочастотных интегральных схемах вы-
полняют в виде полосковых структур. При их расчете используют вспомога-
тельный параметр - эффективную ди-
электрическую проницаемость ε
эфф
, учи-
тывающую вклад диэлектрической про-
ницаемости подложки и находящегося
над ней воздуха. Для узкой полоски ме-
талла (W/h < 1) эта величина определяется
по формуле
где ε
i
- относительная диэлектрическая проницаемость материала подложки,
h — толщина подложки, W — ширина проводящей полоски.
Задавшись приведенными в таблице параметрами h и W, определите
)
/
8
ln(
/
)
4
ln(
)
2
ln(
1
1
1
2
1
1
1
1
1
'
W
h
aa
проницаемость Si, удовлетворяющую указанному значению ε
эфф
Задание 14. Для защиты от вибрации блок само-
летной радиолокационной станции установлен на четы-
рех амортизаторах. Система амортизации при этом мо-
жет иметь до шести собственных механических резонан-
сов, частоты которых определяются уравнения
0
2
4
8
10
12
G
E
D
C
B
A
где A, B, C, D, E, F, G - коэффициенты, определяющиеся параметрами кон-
струкции, со - частота колебаний.
Найдите резонансные частоты для заданных коэффициентов уравнения.
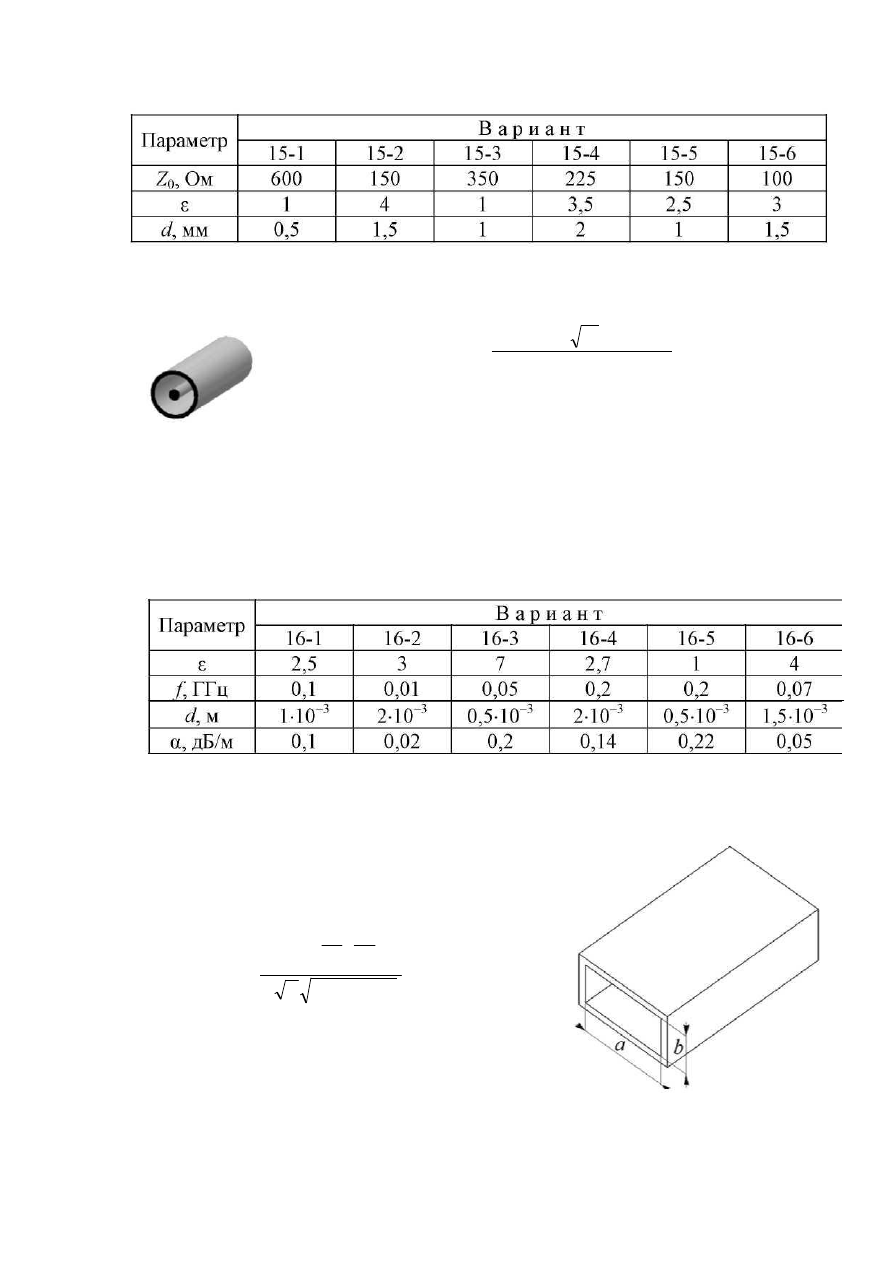
Задание 15. Волновое сопротивление двухпроводной линии рассчиты-
вается по формуле
где ε - относительная диэлектрическая проницаемость среды, в которой нахо-
дится двухпроводная линия, d и D — соответственно диаметры проводников и
расстояние между их осями.
Определите параметр D, обеспечивающий требуемое сопротивление Z
0
при заданных end. Исходные данные приведены в таблице.
2
2
0
1
lg
276
d
D
d
D
Z
Задание 16. Погонные потери мощности в проводниках коаксиальной
линии, выполненной из меди, определяются по формуле
)
/
ln(
)
/
1
(
10
898
,
1
4
d
D
D
d
D
f
где потери а определяются в дБ/м (децибелл на метр), dиD - соответст-
венно диаметры центрального проводника и экрана (измеряются в
метрах), 8 - относительная диэлектрическая проницаемость среды между
проводником и экраном, /- частота (измеряется в гигагерцах).
Задавшись указанными в таблице параметрами е, f и d, определи-
те диаметр D, удовлетворяющий заданному значению а.
Задание 17. Погонные потери мощности в прямоугольном металличе-
ском волноводе, выполненном из меди, для ос-
новного типа волны Ню определяются по фор-
муле
где потери а определяются в дБ/м (децибелл
на метр), a и b - поперечные размеры волно-
вода, X - длина волны. Величины a, b и X в
формулу следует подставлять в сантиметрах.
Задавшись указанными в таблице размерами a и b, определите длину
волны X, удовлетворяющую заданному значению а и условию а<Х< 2a.
2
2
)
2
/
(
1
2
2
1
14
,
0
a
b
a
a
b