Добавлен: 19.10.2018
Просмотров: 3284
Скачиваний: 7

2. УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАБОТЫ
2.1. Подготовка к работе
Изучите методы решения уравнений на ЭВМ, используя указанную ли-
тературу. Обратите особое внимание на следующие вопросы:
1. Виды уравнений и их основные свойства;
2. Основные свойства аналитических и итерационных методов решения
уравнений;
3. Методы исследования уравнений и отделения корней;
4. Итерационные методы поиска корней уравнения на ЭВМ.
2.2. Порядок выполнения работы
1. На основании полученного задания определите вид уравнения, кото
рое требуется решить. Проведите графическое исследование уравнения.
2. Составьте алгоритм решения задачи и подготовьте программу на од
ном из языков программирования высокого уровня.
3. Выполните расчет на ЭВМ с помощью программы.
4. Решите задачу с помощью пакета MathCAD, MATLAB или другого.
Сравните полученный результат с предыдущим решением.
5. Оформите отчет по работе.
2.3. Содержание отчета
1. Цель работы.
2. Задание.
3. Описание метода решения, краткие сведения из теории (формулы,
алгоритм и т.п.).
4. Программа (распечатка), ее описание.
5. Результаты расчета при различных начальных приближениях.
6. Решение с помощью программы и специализированного пакета
(MathCAD, MATLAB и т. п.), сравнение результатов.
7. Краткие выводы по работе.
2.4. Контрольные вопросы
1. Опишите свойства алгебраических и трансцендентных уравнений.
2. Для чего производится процедура отделения корней и предваритель
ное исследование уравнений. Приведите пример.
3. Приведите примеры известных вам способов исследования нелиней
ных уравнений.
4. Опишите основные свойства прямых и итерационных методов реше
ния уравнений.
5. Что понимают под сходимостью итерационной процедуры? Ответ
поясните примерами.
6. Что такое область сходимости применительно к итерационной про

цедуре?
7. Поясните, что такое скорость сходимости и как она связана с эффек
тивностью метода.
8. Опишите метод половинного деления.
9. Опишите метод хорд. Назовите его достоинства и недостатки.
10. Опишите метод секущих. Дайте его сравнительную характеристику.
11. Опишите метод касательных. Укажите его достоинства и недостатки.
12. Опишите метод простой итерации. Дайте его характеристику.
13. Приведите пример итерационного метода, использующего квадра
тичную интерполяцию для решения нелинейных уравнений на ЭВМ.
14. Какие специальные методы применяются для решения алгебраиче
ских уравнений?
15. Почему на практике часто применяют комбинированные алгорит
мы, включающие в себя различные методы отыскания корней?
16. Расскажите об особенностях представления чисел в ЭВМ. Как
влияет способ представления чисел в ЭВМ на точность расчетов?
17. Что такое машинный нуль, машинная бесконечность и
машинное s ? Как эти параметры влияют на точность расчетов на ЭВМ?
18. Для чего используется нормировка уравнений при их решении на
ЭВМ?
19. Назовите три основных источника погрешностей при решении за
дач на ЭВМ, их природу и способы уменьшения.
3. ВАРИАНТЫ ЗАДАНИЙ
Ниже приведены варианты заданий. Каждое из них включает ряд вариан-
тов, отличающихся друг от друга набором исходных данных. Все параметры в
формулах, если не оговорено иное, следует записывать в системе СИ.
Задание 1. Заземлитель в форме кольца радиу-
сом r расположен в грунте на глубине h. Его сопро-
тивление при h » r рассчитывается по формуле
где л = 3,14..., G - электропроводность грунта,
d- диаметр проводника из которого изготовлено
кольцо.
Задавшись параметрами h и d, указанными в таблице, а также приняв
G = 0,03
1
/О
М
∙
M
,
найдите радиус r, обеспечивающий требуемое сопротивле-
ние заземления R.
d
r
h
r
rG
R
16
ln
4
1
2
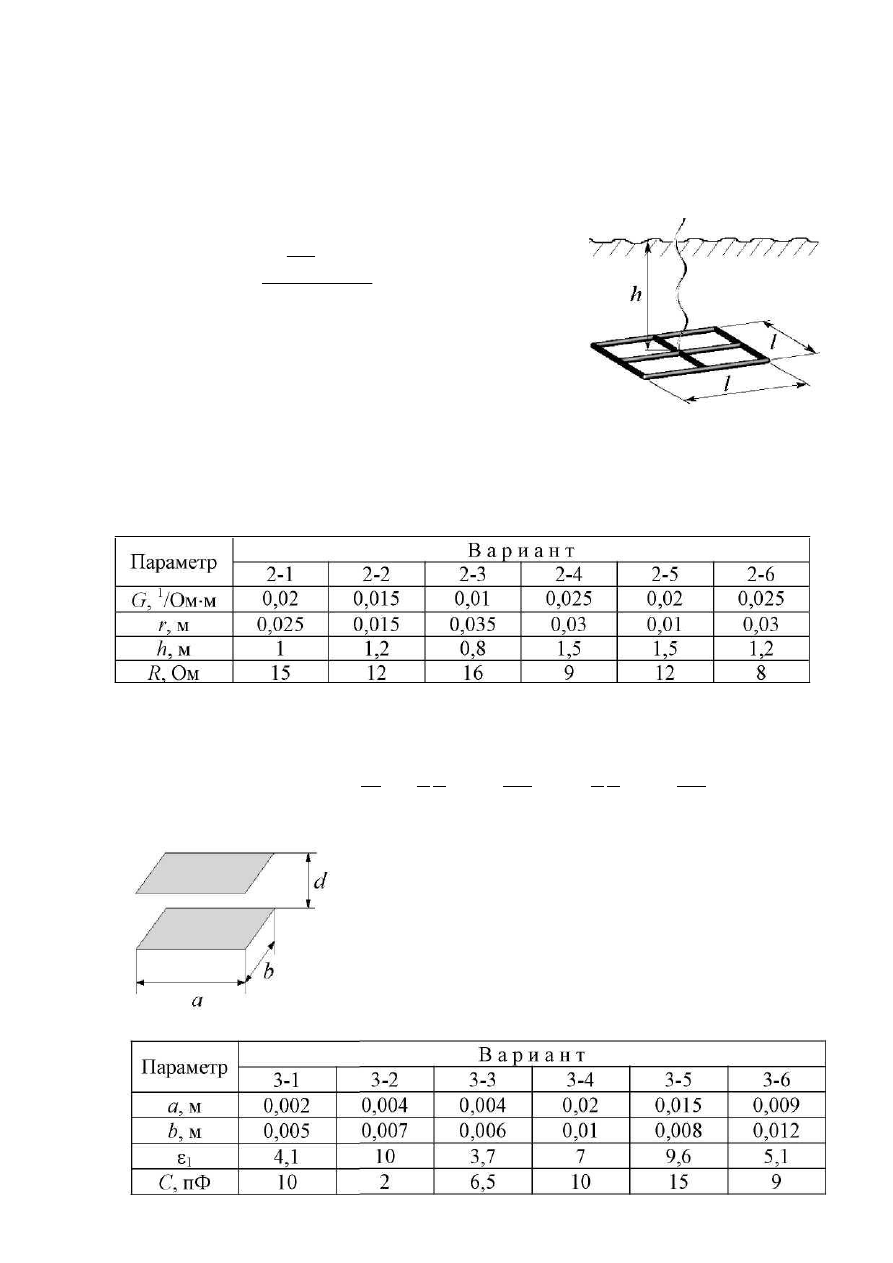
Задание 2. Заземлитель, изготовленный в виде решетки прямоугольной
формы из металлических труб, расположен горизонтально в грунте на глуби-
не h. Сопротивление заземлителя рассчитывается по формуле
где π = 3,14..,, L = 6 х l - суммарная длина труб, r
- радиус труб, h - глубина, G - удельная электро-
проводность грунта.
Задавшись параметрами r = 0,01 м, h (из таблицы), определи-
те размер l, соответствующий требуемому сопротивлению R.
Задание 3. Электрическая емкость системы двух параллельных пластин
прямоугольной формы (см. рисунок) при a >dn b >dможет быть определена
по формуле
d
b
b
d
d
a
a
d
d
ab
С
2
ln
1
1
1
2
ln
1
1
1
0
1
где Si - относительная диэлектрическая проницае-
1
О
мость среды, So = 8,85-10" Ф/м; a и b - размеры
пластин; d - расстояние между пластинами,
71 =
3 , 1 4 . . . .
Найдите зазор d, обеспечивающий получение
требуемой емкости C при указанных в таблице пара-
метрах.
LG
rh
L
R
2
95
,
4
2
ln
2
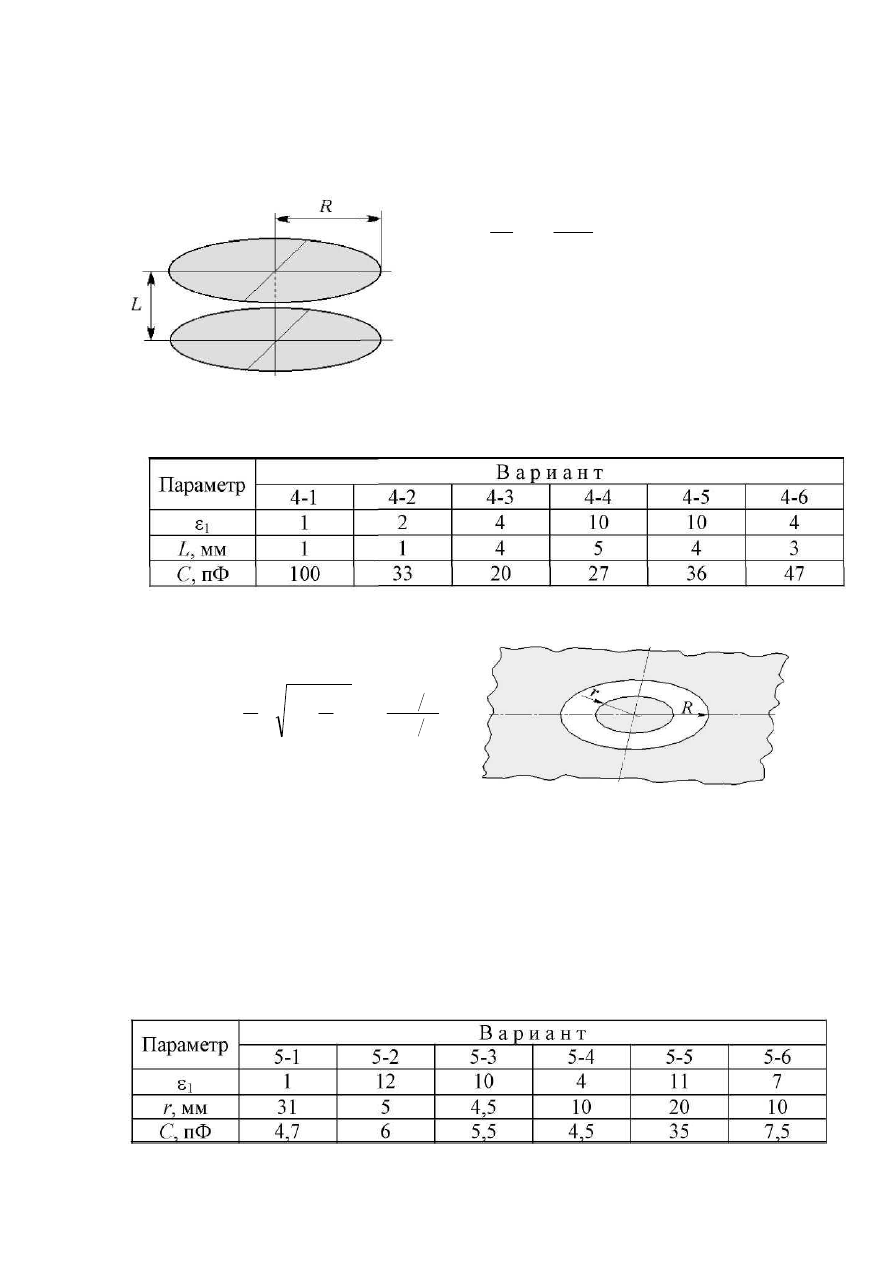
Задание 4. Электрическая емкость двух коаксиальных
плоских дисков (см. рисунок) приL/R<1 рассчитывается по формуле
где ε
1
- относительная диэлектрическая про-
ницаемость среды, ε
0
= 8,85-10
-12
Ф/м, R -
радиус дисков, L - расстояние между диска-
ми, π =3,14... .
Найдите радиус R, удовлетворяющий
требуемому значению емкости С, при заданных в таблице параметрах Si и L .
Задание 5. В интегральных
схемах используют планарные кон-
денсаторы, имеющие вид металли-
ческого диска, расположенного в
круглом вырезе металлизации на
поверхности диэлектрической под-
ложки (см. рисунок). Емкость тако-
го конденсатора определяется по
формуле
где Si - относительная диэлектрическая проницаемость диэлектрика,
So = 8,85-10~
12
Ф/м, R - радиус выреза, r - радиус диска.
Задавшись указанными в таблице параметрами Si и r, найдите
радиус R, обеспечивающий требуемую емкость С. 1
1
16
ln
0
1
L
R
L
R
R
C
R
r
R
r
R
r
R
r
R
C
1
1
ln
1
1
2
2
0
1
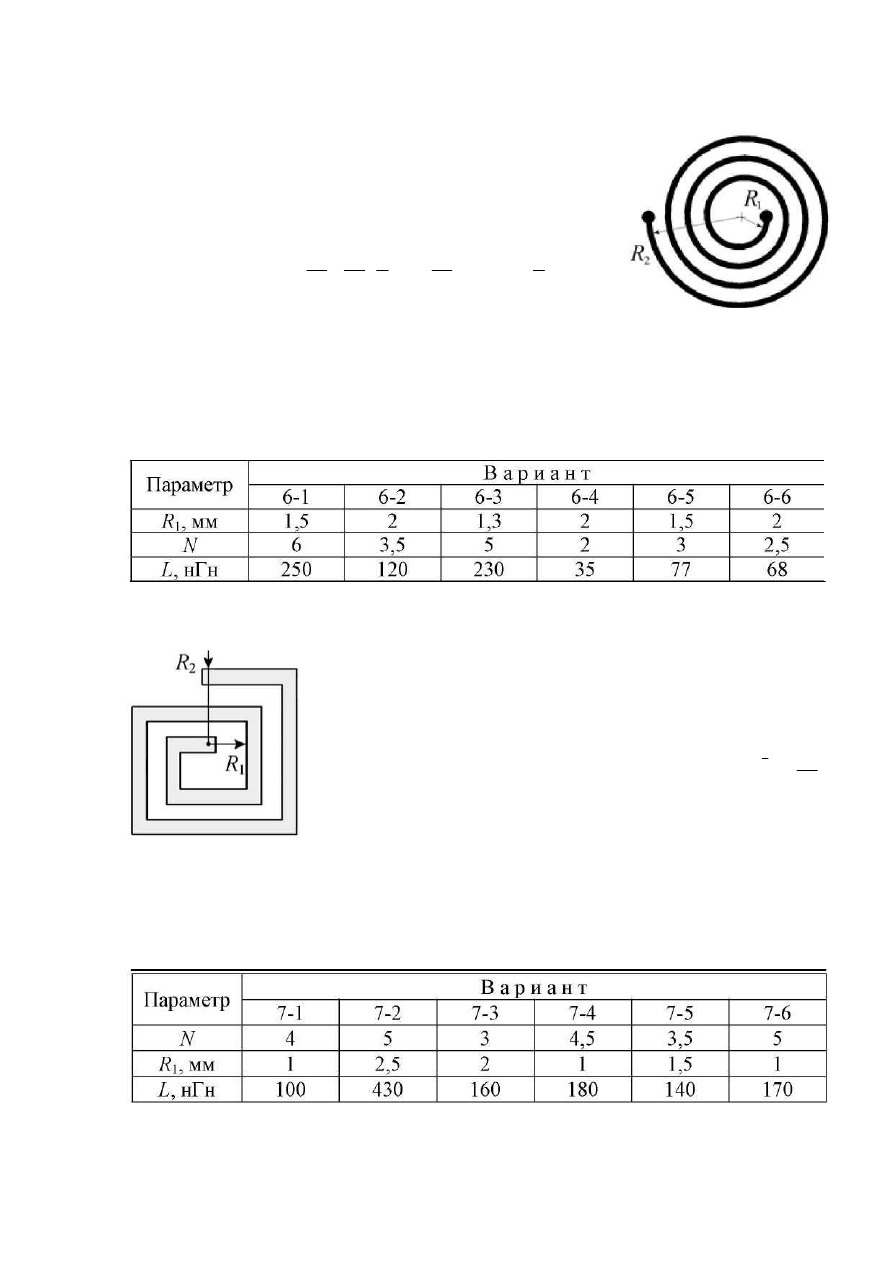
Задание 6. В интегральных схемах используют-
ся плоские катушки индуктивности в виде круглой
металлической спирали. Индуктивность такой ка-
тушки (в наногенри) приближенно определяется по
формуле
где π = 3,14..., N - число витков, a = (R1 + R
2
) / 2,
с = R
2
— R
1
, R
1
и R
2
- внутренний и внешний радиусы. Все размеры в форму-
лах указаны в миллиметрах.
Найдите радиус R
2
, удовлетворяющий требуемому значению индук-
тивности L при указанных в таблице NиR
1
.
Задание 7. В гибридных интегральных схемах исполь-
зуются плоские пленочные катушки индуктивности в
виде квадратной спирали. Индуктивность такой катуш-
ки (в наногенри) приближенно определяется по формулe
где N - число витков, a = (R1 + R
2
) /2, c = R
2
- R1,
R1 и R
2
- размеры внутреннего и внешнего витков катушки. Размеры в фор-
мулах указаны миллиметрах.
Задавшись числом витков N и размером R1,
найдите параметр R
2
, обеспечивающий заданную индуктивность L (значения
N,R1 и L даны в таблице).
2
1
583
,
3
8
ln
24
1
8
ln
4
,
0
2
2
c
a
a
c
c
a
a
N
L
c
a
aN
L
8
ln
14
,
2
3
5