ВУЗ: Пермский национальный исследовательский политехнический университет
Категория: Учебное пособие
Дисциплина: Информатика
Добавлен: 19.10.2018
Просмотров: 12718
Скачиваний: 132

111
Основы математического моделирования
Практически во всех науках о природе, об обществе по-
строение и использование моделей является мощным орудием
познания. Реальные объекты и процессы бывают столь много-
гранны и сложны, что лучшим способом их изучения часто яв-
ляется построение модели, отображающей лишь какую-то грань
реальности и потому более простой, чем эта реальность, и ис-
следование вначале этой модели. Многовековой опыт развития
науки доказал на практике плодотворность такого подхода.
Таким образом, модель представляет собой отражение
имеющихся знаний о процессе или объекте моделирования
в соответствующей форме. Модель строится на основе обоб-
щения известных данных (например, эксперимента) и отражает
лишь те свойства, которые подлежат исследованию. Являясь
результатом анализа и обобщений знаний об объекте, модель
сама становится эффективным средством глубокого исследова-
ния свойств и характеристик объекта, его отношения к другим
объектам, его поведения в различных условиях, в том числе и
таких, которые в действительности воспроизвести или наблю-
дать невозможно.
Математическая модель выражает существенные черты
объекта или процесса языком уравнений и других математиче-
ских средств. Собственно говоря, сама математика обязана сво-
им существованием тому, что она пытается отразить, т.е. промо-
делировать на своем специфическом языке закономерности ок-
ружающего мира.
Математическое моделирование представляет собой метод
исследования объектов и процессов реального мира с помощью
их приближенных описаний на языке математики – математиче-
ских моделей.
Этапы и цели математического моделирования
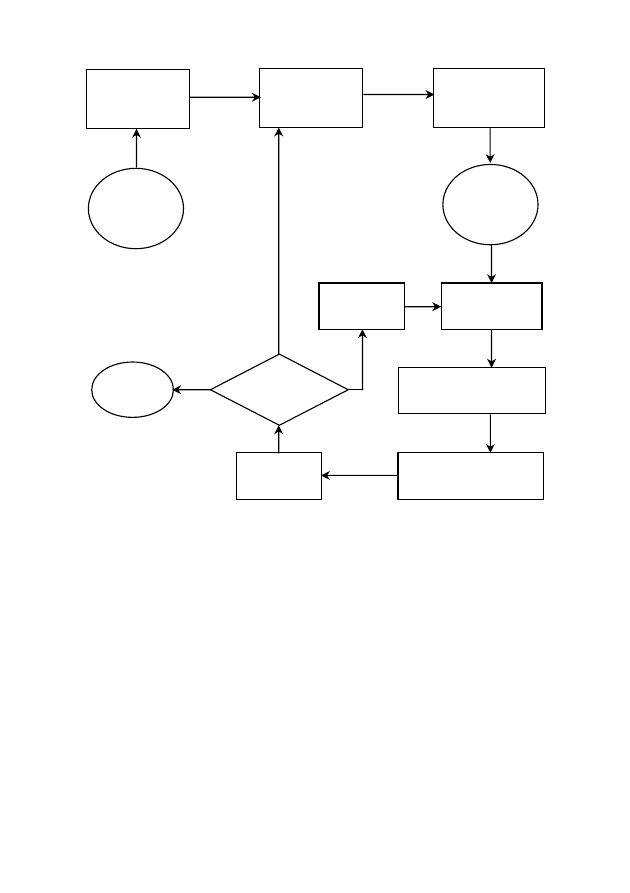
Общая схема процесса математического моделирования
представлена на рис. 15.
112
Рис. 15. Общая схема процесса математического моделирования
Первый этап – определение целей моделирования [10]. Ос-
новные из них:
1) модель нужна для того, чтобы понять, как устроен кон-
кретный объект, какова его структура, основные свойства, законы
развития и взаимодействия с окружающим миром (понимание);
2) модель нужна для того, чтобы научиться управлять объ-
ектом (или процессом) и определить наилучшие способы управ-
ления при заданных целях и критериях (управление);
3) модель нужна для того, чтобы прогнозировать прямые
и косвенные последствия реализации заданных способов и форм
воздействия на объект (прогнозирование).
Исход-
ный
объект
(процесс)
Определение
целей модели-
рования
Огрубление
объекта
(процесса)
Поиск
математического
описания
Матема-
тическая
модель
Выбор метода
исследования
Уточнение
модели
Разработка алгоритма
и программы для ЭВМ
Отладка и тестирова-
ние программы
Расчеты
на ЭВМ
Анализ
результатов
Конец
работы

113
Составим список величин, от которых зависит поведение
объекта или ход процесса, а также тех величин, которые жела-
тельно получить в результате моделирования. Обозначим пер-
вые (входные) величины через х
1
, x
2
,…, x
n
; вторые (выходные)
через y
1
, y
2
,…, y
k
. Символически поведение объекта или процесса
можно представить в виде
1
2
( , , , ),
1, 2, ,
j
j
n
y
F x x
x
j
k ,
где F
j
– те действия, которые следует произвести над входными
параметрами, чтобы получить результаты.
Важнейшим этапом моделирования является разделение
входных параметров по степени важности влияния их изменений
на выходные. Чаще всего невозможно (да и не нужно) учитывать
все факторы, которые могут повлиять на значения интересую-
щих нас величин y
j
. От того, насколько правильно выделены
важнейшие факторы, зависит успех моделирования, быстрота
и эффективность достижения цели. Отбрасывание (по крайней
мере при первом подходе) менее значимых факторов огрубляет
объект моделирования и способствует пониманию его главных
свойств и закономерностей. При этом модель должна быть адек-
ватна исходному объекту или процессу в отношении целей мо-
делирования.
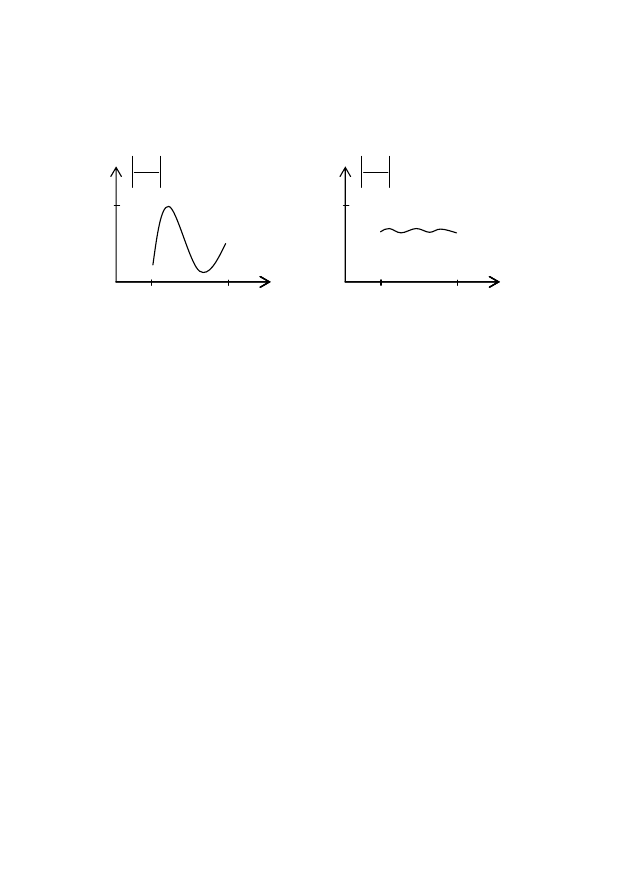
На рис. 16 проиллюстрированы две крайние ситуации:
а) некоторый параметр x
i
очень сильно влияет на результирую-
щую величину y
j
; б) почти не влияет на нее. Ясно, что если все
представляющие интерес величины y
j
реагируют на x
i
так, как
изображено на рис. 16, б, то x
i
является параметром, который
при первом подходе может быть из модели исключен; если же
хотя бы одна из величин y
j
реагирует на изменение x
i
так, как
изображено на рис. 16, а, то x
i
нельзя исключать из числа важ-
нейших параметров.
Следующий этап – поиск математического описания. На
этом этапе необходимо перейти от абстрактной формулировки
модели к формулировке, имеющей конкретное математическое
114
наполнение. В этот момент модель предстает перед нами в виде
уравнения, системы уравнений, системы неравенств, дифферен-
циального уравнения или системы таких уравнений и т.д.
а б
Рис. 16. Варианты степени влияния величины x
i
на результирующую величину y
j
Когда математическая модель сформулирована, выбираем
метод ее исследования. От верного выбора метода часто зависит
успех всего процесса.
Затем разрабатывается алгоритм и составляется программа
для ЭВМ (или используются специализированные пакеты про-
грамм решения математических задач).
Следующий этап – решение простейшей тестовой задачи
(желательно с заранее известным ответом) с целью устранения
грубых ошибок. Это лишь начало процедуры тестирования.
Далее следует собственно численный эксперимент, и выяс-
няется, соответствует ли модель реальному объекту (процессу).
Модель адекватна реальному процессу, если некоторые характе-
ристики процесса, полученные на ЭВМ, совпадают с экспери-
ментальными данными с заданной степенью точности. В случае
несоответствия модели реальному процессу необходимо возвра-
титься к одному из предыдущих этапов.
Один из важнейших этапов математического моделирова-
ния – это выбор метода исследования, а также разработка для
него алгоритма решения задачи.
x
i
b
a
1
m a x
j
j
y
y
b
x
i
b
a
1
m a x
j
j
y
y
b

115
Все методы решения математических задач можно разде-
лить на 2 группы:
1) точные (аналитические) методы решения задач;
2) численные методы решения задач.
Аналитические решения (т.е. представленные формулами,
выражающими результаты исследования через исходные дан-
ные) обычно удобнее и информативнее численных. Однако воз-
можности аналитических методов решения сложных математи-
ческих задач очень ограничены и, как правило, они гораздо
сложнее численных. Численные методы позволяют свести полу-
чение численного решения к последовательному выполнению
большого числа простых арифметических операций над числен-
ными значениями входных данных. При этом результаты вычис-
лений носят приближенный характер. Важно только добиться
того, чтобы ошибки укладывались в рамки требуемой точности.
Численные методы решения нелинейных уравнений
Решение прикладных задач (в расчетах систем автоматиче-
ского управления и регулирования, собственных колебаний ма-
шин и конструкций и др.) часто сводится к нахождению корней
уравнений вида ( ) 0
f x
, где функция f(x) определена и непре-
рывна на отрезке [a,b]. Если f(x) – многочлен, то уравнение на-
зывается алгебраическим, если в f(x) входят тригонометриче-
ские, логарифмические, показательные функции – то трансцен-
дентным.
Аналитического решения многих алгебраических и транс-
цендентных уравнений найти не удается, поэтому используются
приближенные итерационные (численные) методы.
Решение уравнения численным методом сводится к оты-
сканию приближенных значений корней, т.е. к нахождению чис-
ленных их величин, которые с заданной точностью обращают
f(x) в нуль. При этом приходится решать две задачи:
1) отделение корней, т.е. отыскание достаточно малых об-
ластей [a,b], в каждой из которых содержится только один ко-
рень уравнения;