ВУЗ: Пермский национальный исследовательский политехнический университет
Категория: Учебное пособие
Дисциплина: Информатика
Добавлен: 19.10.2018
Просмотров: 12753
Скачиваний: 132

121
Решается система линейных алгебраических уравнений вида
11
1
12
2
1
1
21
1
22
2
2
2
1
1
2
2
...
,
...
,
.................................................
...
n
n
n
n
n
n
nn
n
n
a
x
a
x
a
x
b
a
x
a
x
a
x
b
a
x
a
x
a
x
b
(2)
или в матричной форме:
A x b
,
где
11
12
1
21
22
2
1
2
...
...
...
...
...
...
...
n
n
n
n
nn
a
a
a
a
a
a
A
a
a
a
,
1
2
...
n
x
x
x
x
,
1
2
...
n
b
b
b
b
,
А – матрица коэффициентов системы; x – столбец неизвестных;
b – столбец свободных членов.
Система уравнений (2) путем последовательного исключе-
ния неизвестных приводится к системе уравнений вида
1
12
2
1
1
(1)
2
1
2
(
1)
...
,
...
,
.......................
.
n
n
n
n
n
n
n
x
a
x
a
x
b
x
a
x
b
x
b
(3)
Коэффициенты системы (3) представляют собой треуголь-
ную матрицу с единичной главной диагональю. При этом фор-
мулы пересчета коэффициентов системы на каждом k-м шаге
имеют вид
(
1)
(
1)
(
1)
,
,...,
k
kj
k
kj
k
kk
a
a
j k
n
a
,

122
(
1)
(
1)
(
1)
k
k
k
k
k
kk
b
b
a
,
( )
(
1)
(
1)
(
1)
,
1,..., ;
,...,
k
k
k
k
ij
ij
ik
kj
a
a
a
a
i k
n
j k
n
,
( )
(
1)
(
1)
(
1)
k
k
k
k
i
i
ik
k
b
b
a
b
,
где верхний индекс (k – 1) соответствует предыдущему шагу
прямого хода.
Приведение системы (2) к виду (3) называется прямым хо-
дом метода Гаусса. При этом процесс исключения k-го неиз-
вестного называется k-м шагом прямого хода.
Определение значений неизвестных из системы (3) назы-
вается обратным ходом метода Гаусса и осуществляется по
формуле
( 1)
( 1)
1
,
,
1,...,1
n
i
i
i
i
ij
j
j i
x
b
a
x
i n n
.
(4)
Метод Гаусса с выбором главного элемента заключается в
том, что при прямом ходе производится выбор наибольшего по
модулю (главного) элемента в строке или в столбце матрицы
коэффициентов и соответственно выполняется перестановка
столбцов или строк. Это исключает деление на ноль, если мат-
рица коэффициентов содержит нулевые элементы, и повышает
точность.
При использовании метода Гаусса с выбором главного
элемента в столбце на каждом k-м шаге сначала ищем элемент,
равный
(
1)
max
k
jk
k j n
a
. Пусть это будет элемент
(
1)
k
mk
a
. Меняем мес-
тами k-е и m-е уравнения и производим k-й шаг прямого хода
метода Гаусса.
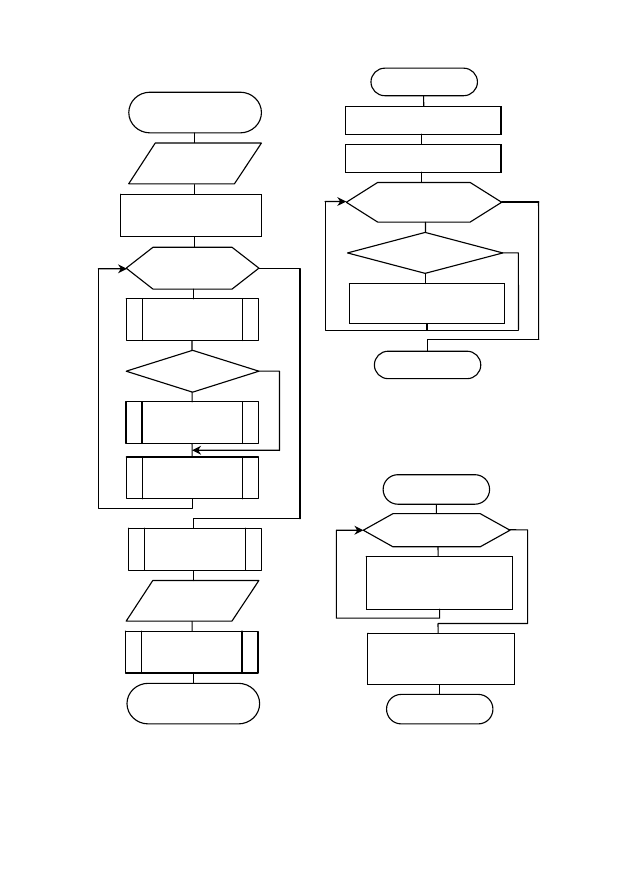
Блок-схема алгоритма решения системы линейных алгеб-
раических уравнений методом Гаусса с выбором главного (мак-
симального) элемента в столбце приведена на рис. 20–25.
123
Рис. 20. Блок-схема основной
программы
Рис. 21. Блок-схема подпрограммы
(П1) поиска главного элемента
в k-м столбце
Рис. 22. Блок-схема подпрограммы
(П2) перестановки k-го
и m-го уравнений при m
0
l = k, n
q = a
k,l
a
k,l
= a
m,l
a
m,l
= q
q = b
k
b
k
= b
m
b
m
= q
Начало
Конец
m = 0
F =
a
k,k
a
j,k
> F
F =
a
j,k
m = j
j = k + 1, n
нет
да
Начало
Конец
Начало
Ввод n,
a(n,n), b(n)
k = 1, n
П1
m
0
П2
П3
П4
Вывод b(n)
Проверка
Конец
нет
да
а1 = а, b1 = b
124
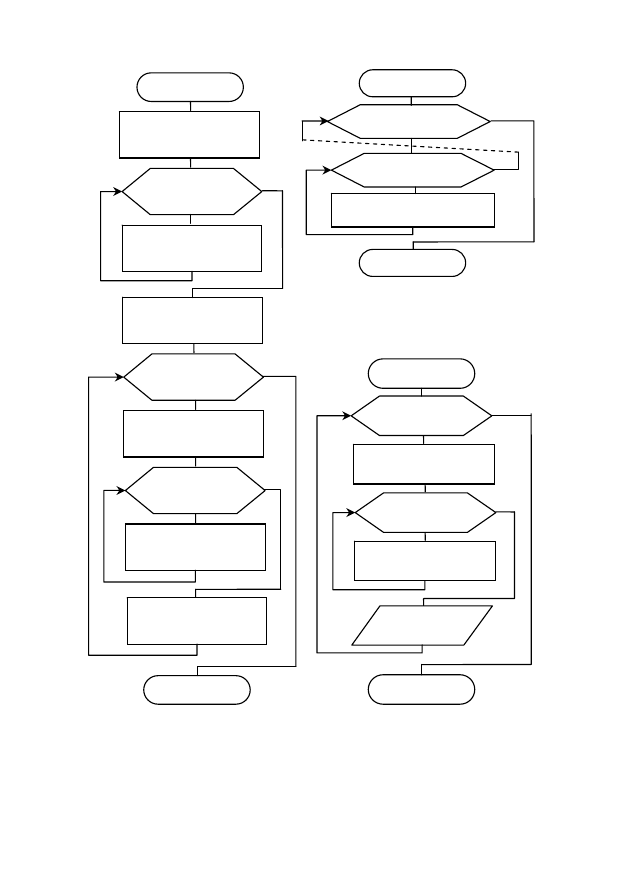
Рис. 23. Блок-схема
подпрограммы (П3) прямого
хода метода Гаусса (приведение
системы к треугольному виду)
Рис. 24. Блок-схема
подпрограммы (П4) обратного
хода метода Гаусса
Рис. 25. Блок-схема
подпрограммы (Проверка)
проверки правильности
решения
Начало
Конец
q = a
k,k
j = k, n
a
k,j
= a
k,j
/q
b
k
= b
k
/q
i = k + 1, n
q = a
i,k
j = k, n
a
i,j
= a
i,j
– a
k,j
q
b
i
= b
i
– b
k
q
i = n – 1,1
j = n, i + 1
b
i
= b
i
– a
i,j
b
j
Начало
Конец
Начало
Конец
i = 1, n
j = 1, n
S = 0
S = S + a1
i,j
b
j
Вывод
S – b1
i

125
Решение задачи интерполяции
Интерполяция или интерполирование – способ нахождения
промежуточных значений величины по имеющемуся дискрет-
ному набору известных значений.
Одним из применений интерполирования является обработ-
ка результатов эксперимента с целью определения аналитиче-
ского вида функции и вычисления ее промежуточных значений.
Задачу интерполяции можно считать обратной задаче табу-
лирования функции. При табулировании по аналитическому вы-
ражению функции находится таблица ее значений.
При интерполяции – по таблице значений (например, полу-
ченных при проведении эксперимента) строится аналитическое
выражение функции
( )
y
f x
для всех значений х на отрезке
[a,b], если известны ее значения y
i
для некоторых точек x
i
этого
отрезка, т.е.
( ),
1,2,...,
i
i
y
f x i
n
, при этом кривая полученной
функции должна проходить точно через имеющиеся точки дан-
ных. Точки x
i
называются узлами интерполяции, а функция
( )
y
f x
– интерполирующей функцией.
Через заданный набор точек можно провести бесконечное
число кривых, поэтому задача интерполяции не имеет единствен-
ного решения, при этом каждая кривая будет описываться своим
аналитическим выражением. Полученную интерполяционную фор-
мулу в дальнейшем можно использовать для приближённого вы-
числения значений функции при значениях аргумента, отличных от
таблично заданных, а также исследовать методами математическо-
го анализа (например, интегрировать и дифференцировать), рис. 26.
На практике чаще всего применяют интерполяцию много-
членами.
При линейной интерполяции считается, что на каждом от-
резке [x
i
,x
i+1
] функция
( )
y
f x
является линейной, представ-
ленной алгебраическим двучленом,
0
1
( )
f x
a
a x
. (5)
В случае если заданы значения в нескольких точках, то по-
лучается кусочно-линейная функция.