Jε(x) = {i ∈ {1, ..., m}: gi(x) ≥ –ε}.

Рис. 4.

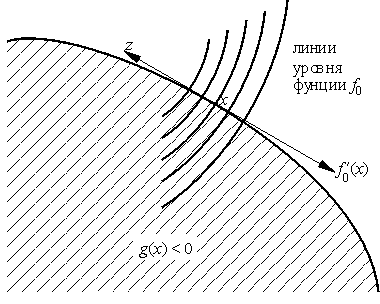
Таким образом, если ε малó и i ∈ J_ε(x), то i-ое ограничение в точке x почти обращается в равенство. В одном из вариантов метода возможных направлений выбирают последовательность ε_n → 0 и из очередной точки xⁿ следующий шаг совершют в направлении zⁿ:

xn+1 = xn + αnzn,

(18)

где zⁿ есть решение следующей линейной задачи

ξ→ min

с ограничениями

(f ′0(xn),z) – ξ ≤ 0,

(g′i(xn),z) – ξ ≤ 0,   i ∈ Jεn(xn)

и нормализующими ограничениями (16). Подчеркнем, что в этой задаче неизвестными являются z и ξ. Длина шага в (18) выбирается таким образом, чтобы точка xⁿ⁺¹ не выходила из множества допустимых точек.

9. Методы проекции градиента

Проекцией P_Ωx точки x ∈ R^m на множество Ω ⊂ R^m называется любая ближайшая к x точка множества Ω:

||x – PΩx|| ≤ ||x – y|| при всех y ∈ Ω.

З а д а ч а  7.10. Докажите, что если Ω замкнуто и выпукло, то для любой точки проекция сужествует и единственна.

З а д а ч а  7.11. Приведите пример, когда проекция: а) не существует; б) не единственна.

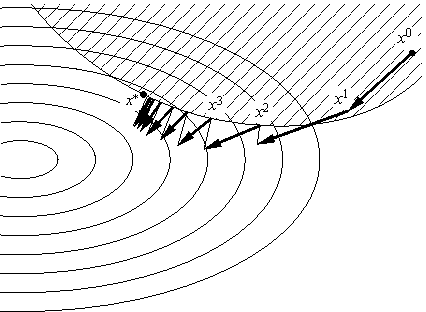
В тех случаях, когда проекцию точки на множество допустимых точек задачи (1), (3) найти достаточно легко (например, когда Ω — линейное подпространство, полупространство, шар, Rm+и  т. д.) используют метод проекции градиента:

xn+1 = PΩ(xn – αnf ′0(xn))

(см. рис. 5), являющийся прямым обобщением градиентного метода.

Рис. 5.

Можно доказать, например, что если функция f₀ ∈ C¹ сильно выпукла и f ′ удовлетворяет условию Липшица, а множество Ω замкнуто и ограничено, то методпроекции градиента сходится со скоростью геометрической прогрессии.

10. Методы линеаризации

Суть этих методов, как следует из названия, состоит в линеаризации минимизируемой функции и ограничений в очередной точке xⁿ строящейсярелаксационной последовательности и объявлении следующим значением xⁿ⁺¹ решения получающейся линейной задачи, т. е. задачи

(f ′0(xn),x – xn) → min,

(19)

gi(xn) + (g′i(xn),x – xn) ≤ 0,   i = 1, ..., l.

(20)

Чтобы эта (линейная) задача была разрешима либо добавляют штраф в минимизируемую функцию, заменяя (19), например, задачей

(f ′0(xn), x– xn) + δ||x – xn||2 → min,

либо добавляя к (20) простые ограничения, которые делают множество допустимых точек этой задачи ограниченным, например, (линейные) ограничения

xi – xni– αn ≤ 0,   –xi + xni– αn ≤ 0   (i = 1, ..., m).

Часто для уменьшения объема вычислительной работы среди ограничений (20) оставляют только ε-активные.

11. Методы штрафов

Основная идея здесь заключается в переходе от задачи (1), (3) к задаче безусловной оптимизации, в которой "наказывается" либо удаление от множества Ωдопустимых точек (внешний штраф), либо приближение изнутри множества Ω к его границе (внутренний штраф). Например, это можно сделать так. Для любого s > 0 определим функцию Fsout:Rm → R равенством (индекс "out" станет понятен чуть ниже)

---

Fsout(x)= f0(x) + s l ∑ i = 1 (gi)2+(x).

(21)

З а д а ч а  7.12 (ср. с задачей 6.11). Пусть f₀, g ∈ C¹, а x* — единственное решение задачи (1), (3). Пусть, кроме того, множество {x ∈ R^m: ||g_i(x)|| ≤ ε, i = 1, ..., l} при некотором ε ≥ 0непусто и ограничено. Докажите, что (безусловная) задача

F sout(x)→ min

(22)

при всех s разрешима и ее решение x^s сходится к x* при s→ ∞.

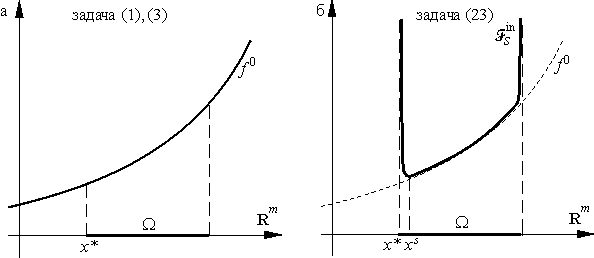
Геометрическая трактовка замены задачи (1), (3) задачей (22) изображена на рис. 6.

Рис. 6.

Задачу (22) решают тем или иным методом решения безусловных задач, увеличивая на каждом шаге штраф s. Как и в случае задач с ограничениями-равенствами, основным недостатком метода штрафов является рост числа обусловленности задачи (22) с ростом s.

Описанный класс методов называют методами внешних штрафов, поскольку минимизируемая функция изменяется вне множества Ω. На несколько другой идее основываются так называемые методы внутренних штрафов или барьеров. Образно его можно описать так: у границы множества Ω возводятся барьеры, не позволяющие приближаться к его границе. Например, вместо задачи (1), (3) можно рассмотреть задачу

Fsin(x)→ min,

(23)

где функция Fsin: Ωg →R определяется равенством (ср. с ((21))

Fsin(x)= f0(x) + s l ∑ i = 1 1 gi(x) .

Сравнение геометрических интерпретаций задач (1), (3) и (23) изображено на рис. 7.

Рис. 7.

З а д а ч а  7.13. Сформулируйте и докажите аналог задачи 7.5 для метода барьеров.

Задача (23) решается методами, развитыми для безусловных задач; при этом "крутизна барьера" характеризуемая числом s, возрастает на каждом шаге.

З а д а ч а  7.14. Попытайтесь выписать аналоги штрафных функций Fsoutи Fsinдля общей задачи нелинейного программирования (1)–(3), содержащей как ограничения-неравенства, так и ограничения-равенства.

12. Двойственные методы

Суть методов из этого весьма обширного класса в применении к задачам с ограничениями-неравенствами, так же как и в задачах с ограничениями-равенствами, заключается в замене условной задачи (1), (3) задачей поиска стационарной (часто седловой) точки функции Лагранжа. В выпуклом случае задача (1), (3) и задача о поиске седловой точки функции Лагранжа в силе теоремы Куна – Таккера эквивалентны. Например, применение простейшего (градиентного) метода к последней задаче приводит к следующему методу Эрроу – Гурвица – Удзавы:

xn+1 = xn – αnL′x(xn,μn), μn+1 = [μn + αnL′μ(xn,μn)]+.

Для поиска седловой точки в двойственных методах применяют почти весь спектр описанных выше методов минимизации — методы Ньютона, квазиньютоновские методы, методы сопряженных направлений и  т. д.

---

Смотрите также файлы

• 6.2. Пример решения задачи целочисленного программирования методом ветвей и границ.docx

• 6.1. Постановка и методы решения задач целочисленного программирования.docx

• 5.5. Методы решения транспортных задач.docx

• 5.4. Некоторые виды задач линейного программирования (транспортная задача, задача о назначениях).docx

• 5.3. Симплекс-метод.docx