ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Лекция
Дисциплина: Моделирование систем
Добавлен: 19.11.2018
Просмотров: 2057
Скачиваний: 18
78
- Что необходимо для построения графа состояний системы массового
обслуживания?
- Что представляет собой граф состояний системы массового обслужи-
вания со схемой «гибели и рождения»?
- Чему равно число состояний в графе состояний системы массового об-
служивания?
- Какой вид имеет система уравнений для определения вероятностей со-
стояний системы массового обслуживания?
- По какому общему правилу вычисляется вероятность любого состоя-
ния системы массового обслуживания?
Примеры решения задач
1. Построить граф состояний системы массового обслуживания и при-
вести основные зависимости ее показателей эффективности.
Решение.
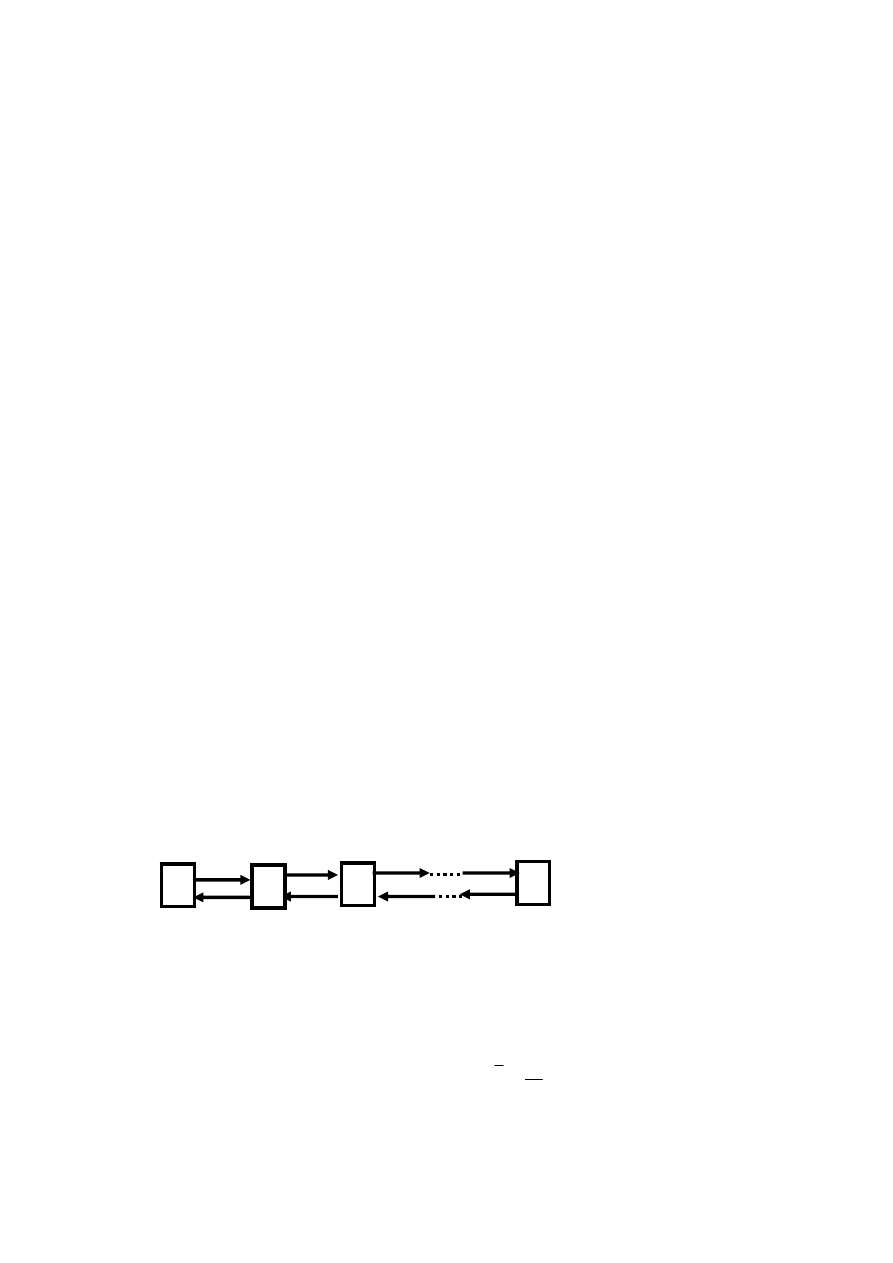
а) n-канальная СМО с отказами (задача Эрланга)
Основные параметры:
- каналов
n
,
- интенсивность потока
λ
,
- интенсивность обслуживания
μ
.
Возможные состояния системы:
0
S
1
S
2
S
n
S
- все каналы свободны (ноль заявок в системе);
- один канал занят, остальные свободны (одна заявка в системе);
- два канала заняты, остальные свободны (две заявки в системе);
...................................................................................
- все каналов заняты ( заявок в системе).
n
n
Граф состояний:
Показатели эффективности системы:
- относительная пропускная способность
n
P
1
q
−
=
,
- абсолютная пропускная способность
q
λ
A
⋅
=
,
- вероятность отказа
n
P
отк
P
=
,
- среднее число занятых каналов
μ
A
z
=
.
б) n-канальная СМО с m-ограниченной очередью
Возможные состояния системы:
λ
λ
λ
λ
μ
μ
2
0
S
1
S
2
S
μ
3
μ
n
n
S
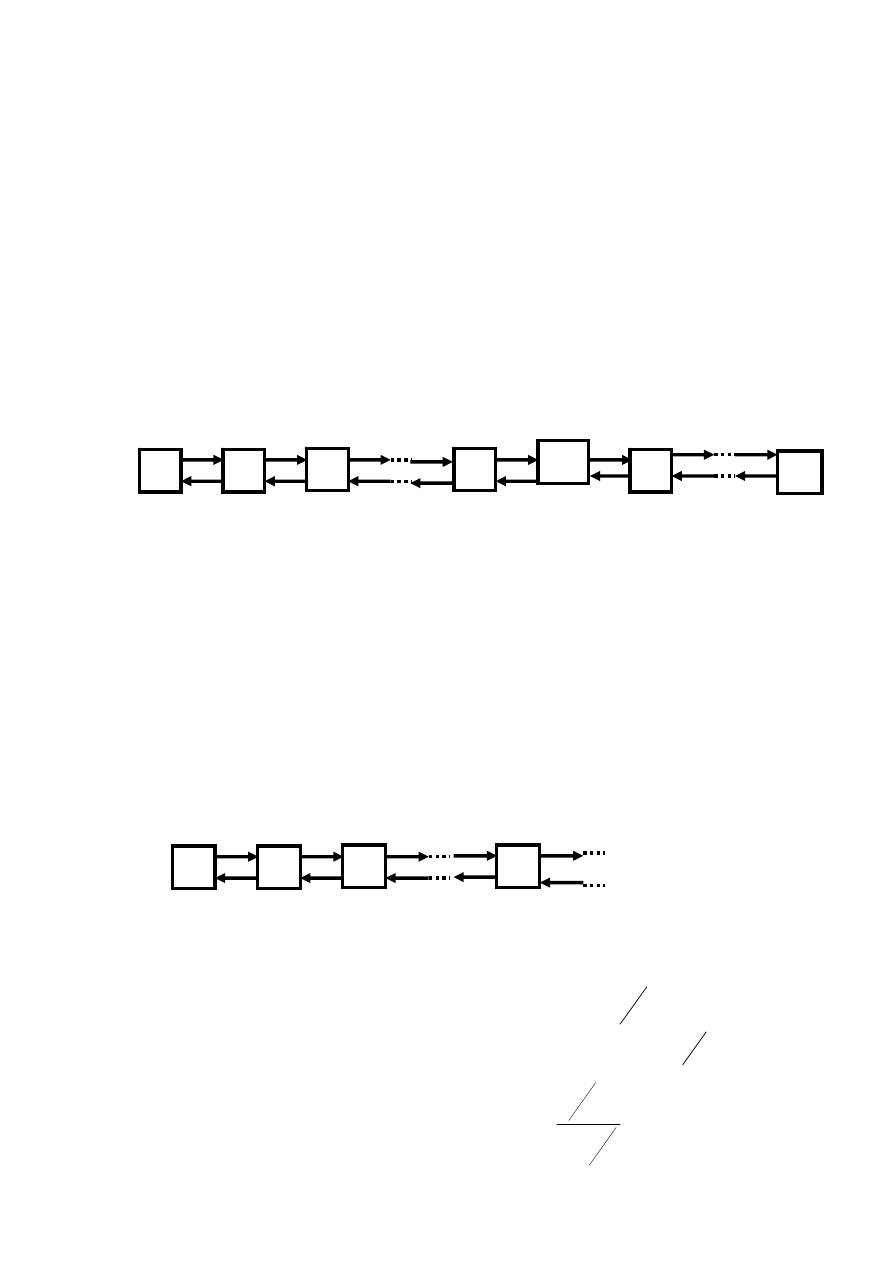
79
0
1
S
S
- все каналы свободны (ноль заявок в системе);
- один канал занят, остальные свободны (одна заявка в системе);
0
S
1
S
2
S
2
S
n
S
n
n
1
n
S
+
2
n
S
+
m
n
S
+
m
0
S
1
S
2
S
n
S
1
−
- два канала заняты, остальные свободны (две заявки в системе);
...................................................................................
- все каналов заняты ( заявок в системе), ноль заявок в очереди;
- все каналы заняты, одна заявка в очереди;
- все каналы заняты, две заявки в очереди;
....................................................................................
- все каналы заняты, заявок в очереди.
Граф состояний:
λ
λ
λ
λ
λ
λ
n
S
1
n
S
+
2
n
S
+
λ
m
n
S
+
0
S
1
S
2
S
n
S
в) Одноканальная СМО с неограниченной очередью
Возможные состояния системы:
- все каналы свободны (ноль заявок в системе);
- канал занят, ноль заявок в очереди;
- канал занят, одна заявка в очереди;
...................................................................................
- канал занят,
n
заявка в очереди;
....................................................................................
Граф состояний:
Показатели эффективности системы:
- среднее число заявок в системе
μ
1
+
,
L
L
очер
сист
=
- среднее время пребывания заявки в системе
( )
сист
L
сист
λ
1
=
W
⋅
,
- среднее число заявок в очереди
μ
1
λ
L
2
очер
−
⎟⎞
⎜
⎝
⎛
=
λ
μ⎠
,
μ
μ
2
μ
3
μ
n
μ
n
μ
n
λ
nμ
μ
n
λ
λ
λ
λ
λ
μ
μ
μ
μ
μ
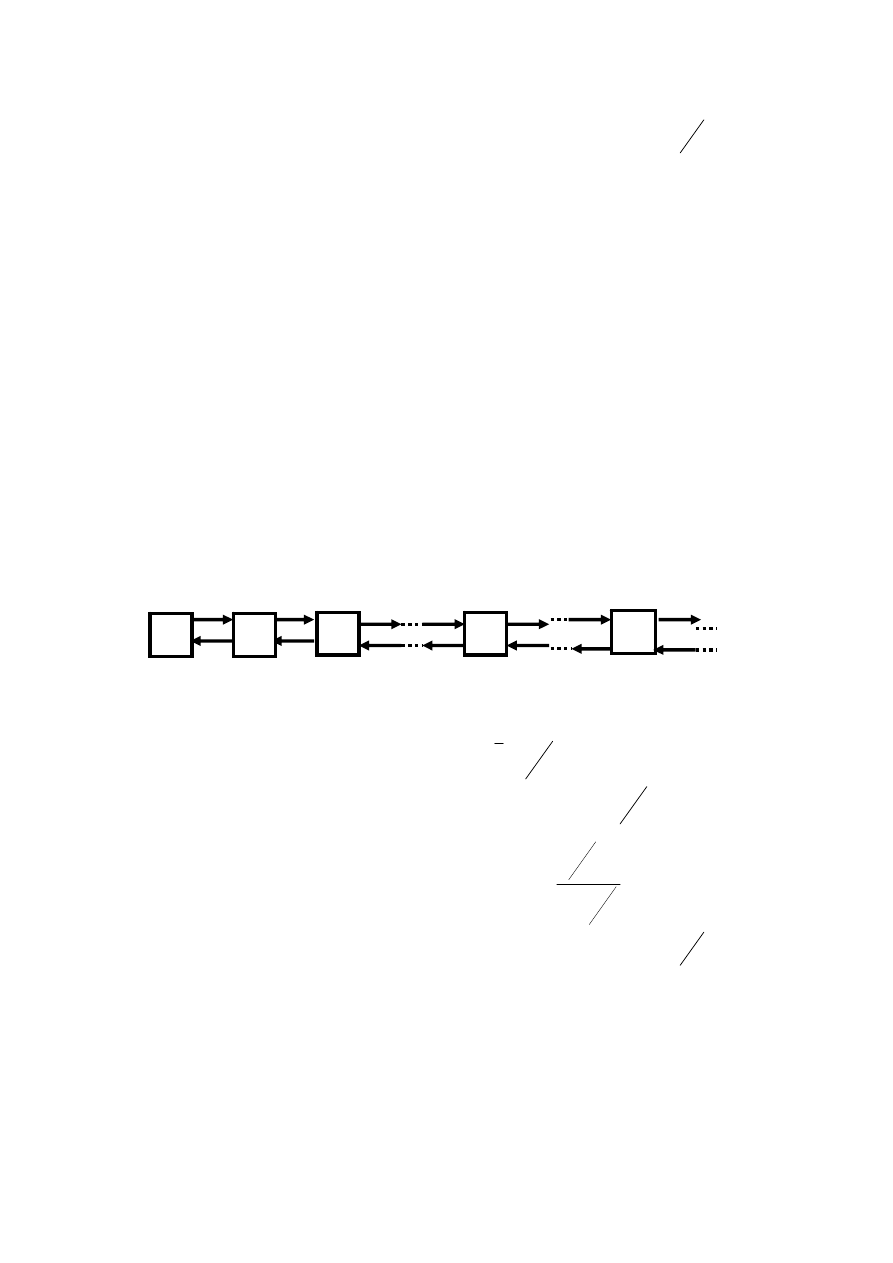
80
- среднее время пребывания заявки в очереди
( )
очер
очер
L
λ
1
W
⋅
,
=
- абсолютная пропускная способность
λ
A
=
,
- относительная пропускная способность
1
q
=
.
г) n-канальная СМО с неограниченной очередью
Возможные состояния системы:
0
S
1
S
2
S
n
S
n
n
1
n
S
+
m
n
S
+
m
- все каналы свободны (ноль заявок в системе);
- один канал занят, остальные свободны (одна заявка в системе);
- два канала заняты, остальные свободны (две заявки в системе);
...................................................................................
- все каналов заняты ( заявок в системе), ноль заявок в очереди;
- все каналы заняты, одна заявка в очереди;
....................................................................................
- все каналы заняты, заявок в очереди;
....................................................................................
Граф состояний:
λ
λ
0
S
1
S
2
S
λ
λ
n
S
λ
λ
m
n
S
+
λ
μ
μ
n
μ
n
μ
n
μ
2
μ
3
μ
n
Показатели эффективности системы:
μ
λ
=
z
,
- среднее число занятых каналов
μ
1
+
,
L
L
очер
сист
=
- среднее число заявок в системе
μ
1
λ
L
2
очер
−
⎟⎞
⎜
⎝
⎛
=
λ
μ⎠
,
- среднее число заявок в очереди
- среднее время пребывания заявки в очереди
( )
очер
L
λ
очер
1
=
W
⋅
.
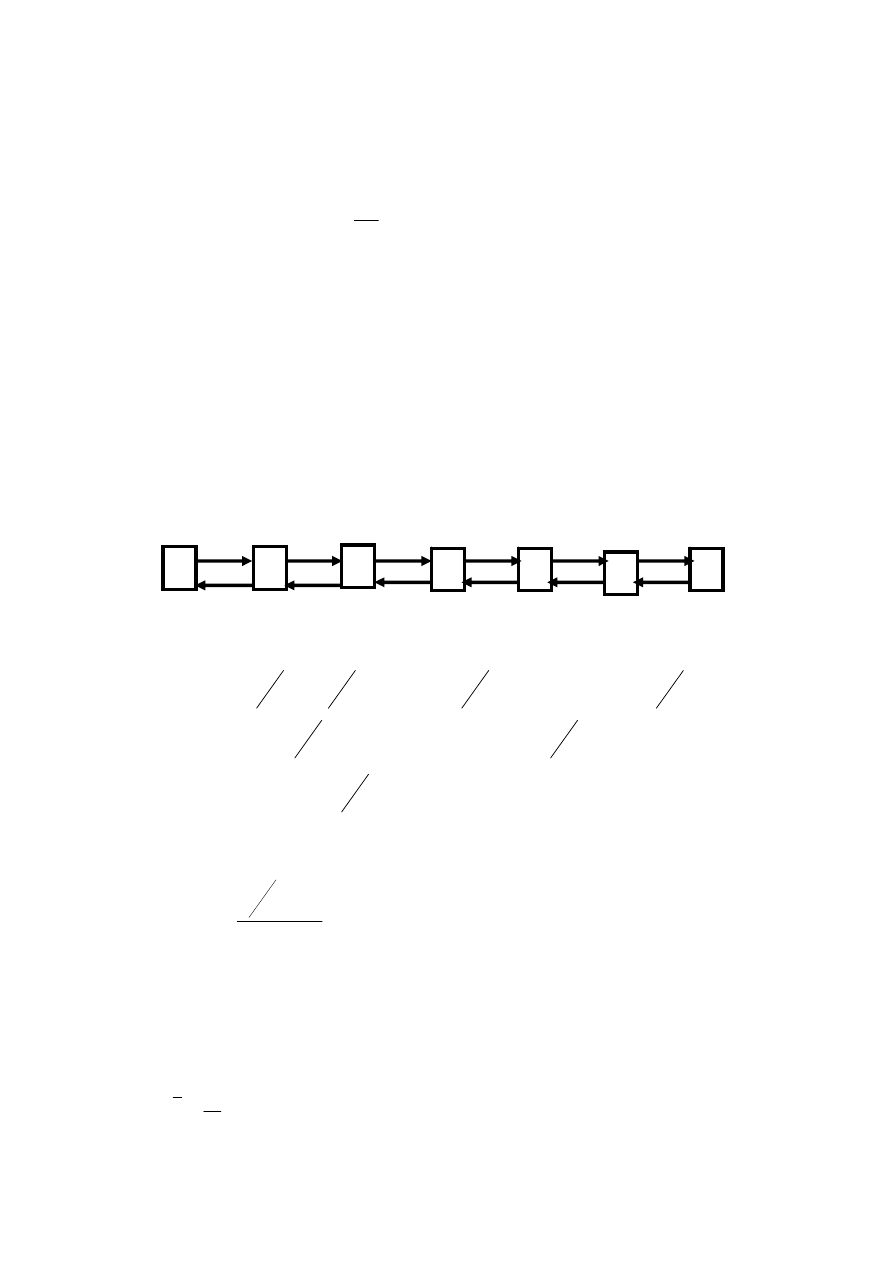
2. Вычислительный центр имеет три ЭВМ. В центр поступает на реше-
ние в среднем четыре задачи в час. Среднее время решения одной задачи -
полчаса. Вычислительный центр принимает и ставит в очередь на решение не
более трех задач. Необходимо оценить эффективность центра.
РЕШЕНИЕ. Из условия ясно, что имеем многоканальную СМО с огра-
ниченной очередью:
81
- число каналов
3
n
=
;
- интенсивность потока заявок
4
λ
=
(задача / час);
- время обслуживания одной заявки
5
.
0
об
t
=
(час / задача), интенсив-
ность обслуживания
2
t
1
μ
об
=
=
(задача / час);
- длина очереди
3
m
=
.
Перечень возможных состояний:
0
S
1
S
2
S
3
S
4
S
5
S
6
S
0
S
- заявок нет, все каналы свободны;
- один канал занят, два свободны;
- два канала заняты, один свободен;
- три канала заняты;
- три канала заняты, одна заявка в очереди;
- три канала заняты, две заявки в очереди;
- три канала заняты, три заявки в очереди.
Граф состояний:
0
S
1
S
2
S
3
S
4
S
5
S
6
S
λ
λ
λ
λ
λ
λ
3μ
3μ
μ
3
μ
3
μ
Рассчитаем вероятность состояния
:
μ
2
.
122
.
0
μ
μ
2
μ
3
μ
3
μ
3
μ
3
λ
λ
λ
λ
λ
λ
μ
μ
2
μ
3
μ
3
μ
3
λ
λ
λ
λ
λ
μ
μ
2
μ
3
μ
3
λ
λ
λ
λ
μ
μ
2
μ
3
μ
3
λ
λ
λ
λ
μ
μ
2
μ
3
λ
λ
λ
μ
μ
2
λ
λ
μ
λ
1
P
0
=
⎟
⎠
⎞
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
+
+
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
⋅
+
+
⋅
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
+
⋅
⋅
+
⎜
⎝
⎛ +
=
Показатели эффективности:
- вероятность отказа (все три ЭВМ заняты и три заявки стоят в очереди)
;
048
.
0
P
!
n
n
μ
λ
P
0
m
n
m
n
m
=
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛
=
+
+
- относительная пропускная способность
;
952
.
0
P
1
q
n
m
=
−
=
+
- абсолютная пропускная способность
;
808
.
3
q
λ
A
=
⋅
=
- среднее число занятых ЭВМ
.
904
.
1
μ
A
z
=
=

82
обс
P
мин
5
дет
24
3. (Задача с использованием СМО с отказами.) В ОТК цеха работают три
контролера. Если деталь поступает в ОТК, когда все контролеры заняты об-
служиванием ранее поступивших деталей, то она проходит непроверенной.
Среднее число деталей, поступающих в ОТК в течение часа, равно 24, сред-
нее время, которое затрачивает один контролер на обслуживание одной дета-
ли, равно 5 мин. Определить вероятность того, деталь пройдет ОТК необ-
служенной, насколько загружены контролеры и сколько их необходимо по-
ставить, чтобы
(* - заданное значение
).
95
,
0
P
*
обс
≥
t
дет/мин,
4
,
0
./ч
обс
РЕШЕНИЕ.
По
условию
задачи
2
/
p
,
2
,
0
=
=
=
λ
λ
, тогда
=
μ
=
=
μ
.
1) Вероятность простоя каналов обслуживания:
1587
0
3
1
2
2
1
0
2
3
2
1
p
2
1
p
p
1
1
P
0
1
3
2
1
0
,
,
!
/
=
+
+
=
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
+
⋅
+
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
−
21
,
0
!
3
/
1587
,
0
2
P
3
отк
=
⋅
=
79
,
0
21
,
0
1
P
обс
=
−
=
1
3
2
2
2
1
2
1
3
2
2
3
2
1
!
/
!
/
!
/
+
=
+
+
+
⋅
⋅
⋅
⋅
+
⋅
⋅
+
+
μ
μ
μ
λ
λ
λ
μ
μ
λ
λ
μ
λ
,
где 0!=1.
2) Вероятность отказа в обслуживании:
.
3) Вероятность обслуживания:
.
4) Среднее число занятых обслуживанием каналов:
58
,
1
79
,
0
2
n
з
=
⋅
=
526
,
0
3
/
58
,
1
k
з
=
=
316
,
0
79
,
0
4
,
0
A
=
⋅
=
95
,
0
P
79
,
0
P
3
n
*
обс
обс
=
≤
=
=
4
n
=
907
,
0
P
,
093
,
0
P
,
14
,
0
P
обс
отк
0
.
5) Доля каналов, занятых обслуживанием:
.
6) Абсолютная пропускная способность:
.
При
. Произведя аналогичные расчеты для
, получим
=
=
=
95
,
0
P
907
,
0
P
*
обс
обс
=
≤
=
95
,
0
P
965
,
0
P
,
035
,
0
P
,
137
,
0
P
*
обс
обс
отк
0
=
≥
=
=
=
3
n
.
Так как
, то произведя расчеты для
, полу-
чим
5
n
=
.
ОТВЕТ. Вероятность того, что при
= деталь пройдет ОТК необслу-
женной, составляет 21%, и контролеры будут заняты обслуживанием на 53%.
Чтобы обеспечить вероятность обслуживания более 95%, необходимо не
менее пяти контролеров.
4. (Задача с использованием СМО с неограниченным ожиданием.) Сбер-
касса имеет трех контролеров-кассиров (
n 3
= ) для обслуживания вкладчи-