Добавлен: 28.11.2018
Просмотров: 8371
Скачиваний: 76
Для пояснения изложения полезно привести пример. Пусть мы хотим написать программу для машины Тьюринга, которая будет строить сумму двух целых чисел. Целое число п будет изображаться на ленте n последовательными значками * (отсутствие звездочек соответствует нулю), два исходных числа будут разделены запятой, и если исходные данные представляют n + m, то результатом должны быть n + m звездочек, расположенных у левого края ленты. Так, чтобы вычислить 7 + 4, следует записать в качестве исходных данных
*******,****
результатом должно быть
***********
Структура программы проста. Сначала головка движется вправо в поисках запятой (не забывайте, что первоначально головка стоит над крайней левой ячейкой исходных данных). Запятая заменяется звездочкой, и головка продолжает движение, отыскивая пробел, ограничивающий справа исходные данные. Головка возвращается на одну ячейку назад и записывает пробел на место находящейся там звездочки, после чего программа завершается. Легко видеть, что при построении суммы одна звездочка добавляется в середине и одна убирается с правого края. Программа приведена в табл. 11.1.
|
|
Таблица 11.1. Программа для машины Тьюринга
|
Старое состояние |
Старая литера |
Новое состояние |
Новая литера |
Перемещение |
|
1 |
* |
1 |
* |
Вправо |
|
1 |
, |
2 |
* |
» |
|
1 |
ø |
4 |
ø |
На месте |
|
2 |
* |
2 |
* |
Вправо |
|
2 |
, |
4 |
ø |
На месте |
|
2 |
ø |
3 |
ø |
Влево |
|
3 |
* |
3 |
ø |
На месте |
|
4 |
ø |
4 |
ø |
» » |
Чтобы изобразить состояние машины Тьюринга, можно напечатать все ячейки ленты, которые когда-либо рассматривались, и среди них — текущее состояние непосредственно слева от ячейки, находящейся под головкой в данный момент; такой способ мы будем считать стандартным. Мы получаем моментальный снимок; следующий пример показывает начало сложения 2 и 3:
1**,***
На рис. 11.1 показана последовательность моментальных снимков для всего вычисления. Отметим, что программа останавливается в состоянии 3, поскольку в ней не предусмотрены действия для пробела. Состояние 4 возникает только, если в исходных данных имеется ошибка; в этом случае машина попадает в бесконечный цикл. Убедитесь, что программа работает, если любое из исходных чисел (или оба) равно нулю.

Рисунок 11.1. Последовательность моментальных снимков.
Наш пример программы может показаться слишком простым. Попробуйте изменить программу, чтобы она выполняла не сложение, а умножение. Для машины Тьюринга единичная система счисления более естественна, чем любая другая; программа сложения десятичных чисел будет длиннее и сложнее. В литературе, указанной в библиографии, можно найти гораздо более подробный материал о машине Тьюринга и обоснование того, что машина Тьюринга может выполнить любое вычисление, выполнимое на какой-либо другой машине. Вы обнаружите небольшие отличия в разных описаниях машины Тьюринга и там же — доказательства того, что эти отличия ни на что не влияют.
Тема. Напишите универсальный имитатор машины Тьюринга. Входными данными будут: программа для машины Тьюринга, ее исходные данные и (по причине, которая будет объяснена позже) начальное состояние машины. Результатом должны быть трассировка работы машины и ее окончательное состояние. Поскольку машина Тьюринга вовсе не всегда останавливается, причем заранее нельзя предсказать, остановится она или нет (если вы не понимаете, почему это так, обратите внимание на проблему остановки), необходимо как-то контролировать объем печати имитатора и расходуемое им время. Проверьте имитатор на нескольких программах, аналогичных рассмотренным выше.
Хотя в нашем описании именами состояний были положительные целые числа, ваш имитатор должен допускать в качестве имени состояния произвольный идентификатор. В предыдущем примере мы могли бы назвать состояния Начало, ДвижениеВправо, Конец и Ошибка, тогда одна из команд могла бы иметь вид
ДвижениеВправо ø Конец ø Влево
Теперь у нас нет выделенного первого состояния, поэтому его должен указать пользователь.
Указания исполнителю. При разработке данной программы, как и любого имитатора, перед нами стоит проблема эффективности. Если на протяжении всего выполнения используются имена состояний, то постоянно требуемый поиск займет значительное время. Скорость выполнения будет наибольшей, если представить программу для машины Тьюринга в виде двумерного массива, индексами в котором будут состояния и литеры. Элементы массива содержат команду, которую нужно выполнить; элемент специального вида указывает, что соответствующая пятерка отсутствует. Тут, конечно, определенную трудность представляет незнание необходимого размера этого массива до того, как будут прочитаны исходные данные. Отметим также, что необходимо проверить непротиворечивость исходных данных, т. е, убедиться, что никакие две пятерки не начинаются одной и той же парой состояние-литера.
Трассировочная информация должна печататься после каждого изменения состояния. Она должна включать в себя: содержимое всей ленты до самого правого непробела или до головки, в зависимости от того, что находится правее, положение головки и текущее состояние. Вероятно, содержимое ленты следует напечатать на одной строке, а указатель головки и состояние — на следующей. Руководствуйтесь соображениями красоты и ясности. Алфавит ленты, т. е. множество символов, которые могут появляться на ленте, есть просто набор литер, встречающихся где-либо во второй или четвертой компоненте пятерки. Программа должна позволять использовать любую нормальную литеру, имеющуюся в вашей системе. В алфавит всегда входит пробел. Его непросто изобразить в исходных данных, а появляясь в выходной строке, пробелы могут вносить неразбериху. Проблему с вводом можно обойти, если, например, разделять пять компонент команды запятыми. Работа со значащими пробелами часто вызывает затруднения. В естественных языках пробелы осмысленны, но обычно лишь как разделители слов, а не как полноправные символы. Таким образом не существует какого-либо стандартного соглашения об употреблении пробелов в качестве символов.
Тема 12: Стратегия компьютера при игре в калах
Дискуссии о «разумном» поведении компьютеров начались задолго до появления реальных вычислительных машин. Многие согласятся, что высокое мастерство в какой-либо интеллектуальной игре, не поддающейся полному анализу, должно свидетельствовать о незаурядных умственных способностях игрока. Если компьютер к тому же обучаем, то отрицать его интеллект еще труднее. Говоря о машинной игре, чаще всего имеют в виду шахматы, однако даже самые лучшие программы оказываются на уровне весьма посредственных шахматистов. Но в других играх можно достичь большего успеха.
Калах, известный также и под другими названиями (манкала, вари, овари), — это старинная африканская игра. По ее теории написано очень мало, тем не менее в течение столетий в калах играют с помощью камешков представители самых разных культур. Хотя игра эта — чистая борьба умов, не содержащая какого-либо случайного элемента, африканцы режутся в нее постоянно. Благодаря нехитрому инвентарю и простым правилам, калах великолепно подходит и для игры с машиной. Как показывают современные исследования, компьютер с программой наподобие предлагаемой здесь играет в калах лучше любого человека.
Игровое поле для калаха схематически изображено на рис. 12.1. Игроки (их двое) садятся друг против друга. Каждому игроку принадлежат шесть малых лунок вдоль длинной стороны поля и одна лунка большего размера по его правую руку, называемая калахом. В начале игры в каждую малую лунку помещается некоторое количество к камней (для k ≤ 3 известно полное решение; африканцы обычно используют k = 6). Ход игрока заключается в том, что он забирает все камни в одной из малых лунок на своей стороне и раскладывает их по одному в остальные лунки, двигаясь против часовой стрелки. Первый камень кладется в лунку справа от той, из которых взяты камни, затем в следующие, включая свой калах и малые лунки противника, но не калах противника. Может случиться (и это допускается правилами), что раскладывая камни, мы обойдем всю доску и вернемся в исходную лунку или даже пройдем дальше. На рис. 12.2а и b, показаны позиции до и после выполнения такого циклического хода.
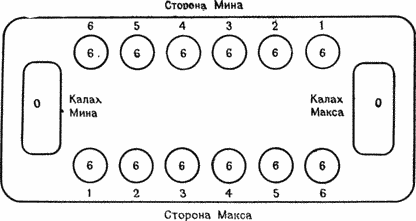
Рисунок 12.1. Игровое поле для калаха. Числа в лунках показывают количество находящихся там камней.
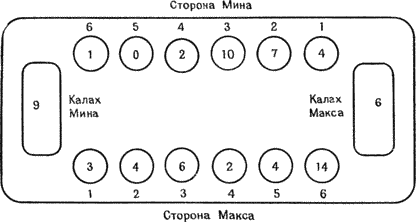
Рисунок 12.2а. Перед циклическим ходом Макса. Макс ходит из лунки 6.
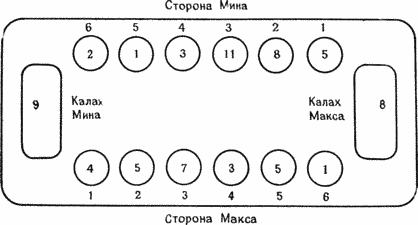
Рисунок 12.2b. После циклического хода Макса. Калах Макса пополнялся дважды.
Есть два дополнения к правилу выполнения хода. Если последний камень попал в одну из непустых малых лунок игрока, делавшего ход, причем камни клались и в лунки противника, то делается повторный ход из лунки, в которую попал последний камень, по тем же правилам, что и первый. Игрок может сделать сколь угодно длинную серию повторных ходов. Если последний камень попал в одну из малых лунок противника, и в этой лунке стало два или три камня, то эти камни берутся в плен и помещаются в калах игрока, сделавшего ход. Если при пленении в предыдущей лунке также оказалось два или три камня, то и они забираются в плен. Теоретически игрок может за один ход полностью очистить сторону противника. Игра оканчивается, как только в калахе одного из игроков окажется больше половины всех камней (заметим, что если камень попал в калах, то он уже никогда его не покинет). Если у игрока, получившего очередь хода, не осталось ни одного камня в малых лунках, то игра немедленно прекращается и все камни противника попадают в калах противника. На рис. с 12.3 по 12.5 показаны некоторые типичные ходы.
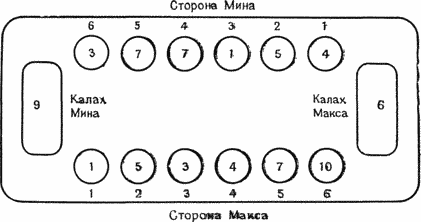
Рисунок 12.3a. Серия ходов из лунки 6 Макса. Последний камень попадает в лунку 3 Макса, и из этой лунки делается повторный ход.
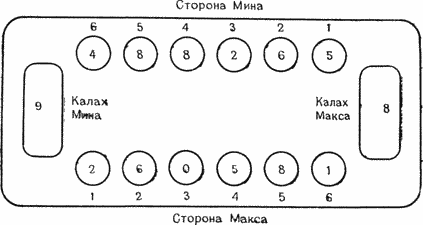
Рисунок 12.3b. После серии ходов. Камни из лунки 3 разложены в следующие лунки.
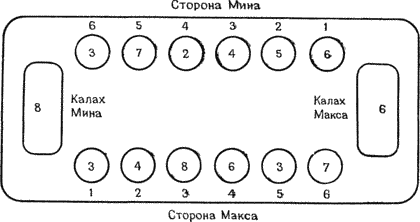
Рисунок 12.4а. Перед взятием в плен камней Мима. Ходом из лунки 3 Макс попадает в лунку 4 Мина.
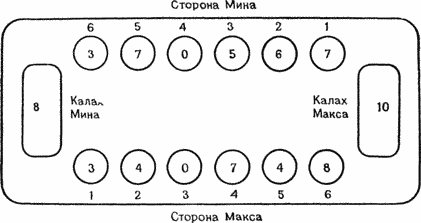
Рисунок 12.4b. После взятия в плен камней из лунки 4 Мина. В калах Макса один камень попадает при раскладывании камней и еще три — при пленении.
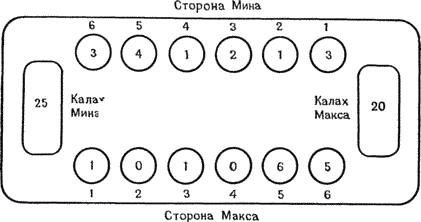
Рисунок 12.5а. Многократный захват пленных Максом. Камни из лунок Мина 2, 3 и 4 берутся в плен одним ходом из лунки 6.
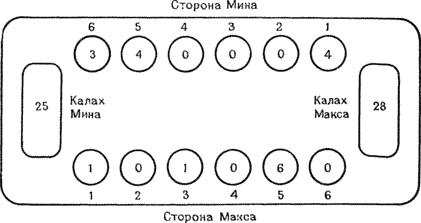
Рисунок 12.5b. Макс почти опустошил лунки Мина. Отметим, что Макс мог бы сделать ход с пленением из лунки 5 вместо лунки 6.
Программа для проверки правильности хода весьма проста. Выбор игрока ограничен максимум шестью возможностями для хода. После того как начальная лунка выбрана, легко находятся повторные ходы и взятия в плен. Для проверки окончания игры после хода надо лишь сравнить калах игрока, делавшего ход, с половиной общего числа камней. Конечно, отсюда никоим образом не следует, как находить наилучший в данной позиции ход.
Основная идея выбора хода состоит в построении дерева всех возможных продолжений из заданной позиции. Затем мы выбираем такую ветвь дерева, которая обеспечивает в конце концов победу. Для простоты изложения и еще по одной причине, которая вскоре станет понятной, мы будем называть компьютер Максом, а его противника — Мином. Предположим, что где-то в середине игры настала очередь хода компьютера. Макс может попытаться оценить положение, испробовав поочередно каждый из шести возможных ходов. Если один из них сразу же приводит к выигрышу, то Максу, очевидно, следует делать именно этот ход. Но что делать Максу, если ни один ход не ведет к немедленной победе? Как выбрать ход?
Максу следует проанализировать каждый ответ Мина на свои ходы. Допустим, один из этих ответов приводит к выигрышу Мина. Со стороны Макса было бы глупо делать ход, дающий Мину шанс на немедленную победу (хотя иногда Максу не избежать этого). В таком случае Макс узнает, какие ходы не делать. Однако, чтобы выбрать, какой ход делать, Максу придется построить еще один уровень ответов на ответы Мина к исходным ходам Макса. Если можно найти выигрышный ответ для некоторого множества ответов Мина, то Максу следует выбрать тот первоначальный ход, при котором Мину остаются только ответы, для которых есть выигрышный ответ Макса (помните дом, который построил Джек?). Если все это непонятно, попробуйте найти ходы, ответы и ответы на ответы для позиции с рис. 12.6.
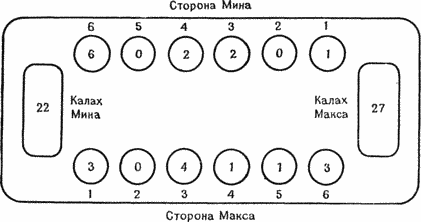
Рисунок 12.6а. Ход Макса. Макс ходит из лунки 1.
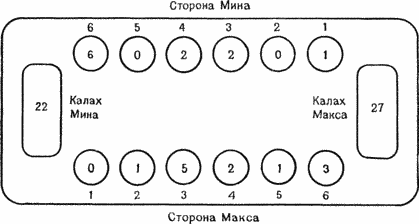
Рисунок 12.6b. Результат хода Макса. Мин отвечает ходом из лунки 6.
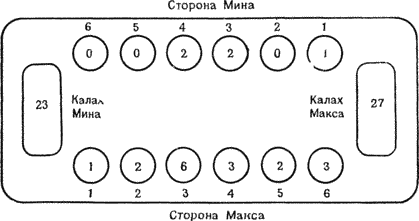
Рисунок 12.6с. Позиция после ответа Мина. Макс отвечает ходом из лунки 2.
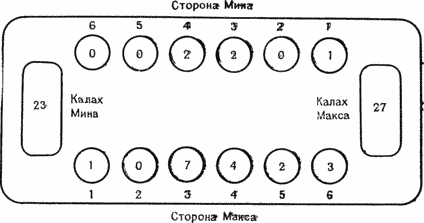
Рисунок 12.6d. Позиция после ответа Макса. Это всего лишь одна из примерно б3 подобных цепочек ходов.