Добавлен: 28.11.2018
Просмотров: 8370
Скачиваний: 76
Однако может оказаться недостаточным заглядывать вперед на два уровня. Несмотря на то что игра в калах обязательно кончается, предсказать, насколько далеко нужно заглянуть вперед, чтобы найти конец, оказывается весьма трудно. Каждый следующий уровень требует примерно в шесть раз больше времени и памяти, чем предыдущий. Надо что-то предпринять, чтобы остановить этот рост.
Этой цели служит статическая оценочная функция, дающая оценку позиции без построения дерева. В калахе мы воспользуемся разницей очков, получаемой как разность числа камней в калахах Макса и Мина. Если слегка изменить правила, потребовав, чтобы в калах победившего игрока сразу же перекладывались все камни, то разница очков всегда будет положительной, когда Макс имеет преимущество, а когда Макс выиграет, разница очков станет максимально возможной. Теперь Макс может выбирать тот из шести ходов, который максимизирует (не зря его зовут Макс) статическую оценочную функцию. Если два хода одинаковы с этой точки зрения, Макс может выбрать любой из них случайным образом.
Ну вот мы и ответили на вопрос о стратегии Макса. Так ли это? Если бы этим исчерпывалась стратегия калаха, то такая игра немногого бы стоила. Ведь Мин может ставить Максу ловушки, и, чтобы их избежать, Максу нужно смотреть вперед. Статическую опенку можно применять к позициям, лежащим глубоко в дереве и не являющимся заведомо выигрышными или проигрышными.
Пусть Макс хочет заглянуть вперед на d уровней. Будем считать, что начальная позиция лежит на уровне 0. Постройте все шесть мыслимых ходов, приводящих нас на уровень 1. Применяя в каждой позиции уровня 1 ходы Мина, получите все позиции уровня 2.
Продолжайте в том же духе, пока не построите все дерево вплоть до уровня d. Иногда может оказаться, что не все шесть ходов возможны, поскольку одна или несколько лунок пусты. Кроме того, некоторая ветвь может окончиться из-за хода, завершающего игру. Заметим, что все ходы на четных уровнях делает Макс, а на нечетных — Мин.
Теперь, чтобы перенести оценку с уровня d на уровень 0, выполните следующие действия на всех уровнях, начиная с уровня d и кончая нулевым. Примените статическую оценочную функцию ко всем листьям на рассматриваемом уровне. Это дает разницу очков в листьях. Для нелистовых узлов постройте оценку разницы очков, найдя максимум оценок по всем непосредственным преемникам данного узла, если он находится на четном уровне, и минимум, если узел — на нечетном уровне. Такой способ действий отвечает стремлению Макса максимизировать разрыв и стремлению Мина минимизировать его (или сделать более отрицательным). После того как пройден весь путь до нулевого уровня и найдена разница очков в исходном узле, выберите любой из шести ходов, позволяющий получить эту разницу очков. Отметим, что, как правило, все листья будут находиться на уровне d. Кроме того, при построении дерева можно всегда проходить каждую ветвь сначала вглубь,т.е. строить дерево в порядке перебора в глубину, а не в порядке перебора в ширину, как описано[19]. На рис. 12.7 показана часть возможного дерева игры. До листьев доведена лишь одна ветвь. Изображены правильные значения, вычисленные исходя из показанной на рисунке информации. Максу следует выбрать ход из лунки 1.
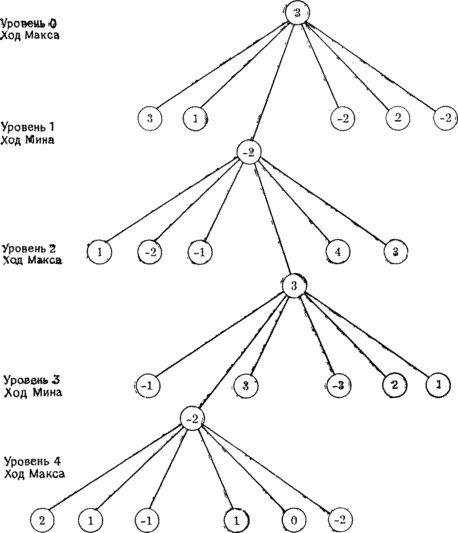
Рисунок 12.7. Возможное дерево игры. Полностью показан только один путь до низа дерева. Предполагается, что значения в кружках получены из анализа нижних уровней.
По сути дела, мы сейчас описали минимаксную процедуру для игры двух лиц. Как нетрудно видеть, для анализа на d уровней вперед необходимо построить около
![]()
позиций. Ввиду очень быстрого роста этой функции желательно иметь какое-либо средство, экономящее усилия. Альфа-бета-процедура при том же объеме работы позволяет иногда провести анализ на вдвое большую глубину.
Идея этой процедуры обобщает рассмотренный пример. Допустим, что в некотором внутреннем узле А дерева ход должен сделать Макс и что он с помощью перебора в глубину уже построил полное дерево В для хода из лунки 1 и дерево С для хода из лунки 2. Предположим далее, что оценка, вычисленная при анализе дерева, равна 1 для узла В и 2 — для С. Тогда можно приписать узлу А предварительную оценку (ПО), равную 2. Что бы ни случилось, Макс может отвергнуть любой ход из А с оценкой меньше 2. Допустим теперь, что Макс начинает строить дерево для хода из лунки 3 в узел D. В узле D ход Мина. Как только D получит ПО, равную или меньшую 2, дальнейшее построение дерева ниже D окажется уже ненужным. Действительно, Мин заведомо не выберет ход с оценкой больше 2, если доступно значение 2 или меньше. Но тогда узел D не будет интересовать Макса, коль скоро он уже имеет возможность получить 2. Итак, можно прекратить раскрытие узла D. Обсуждавшееся дерево показано на рис. 12.8.
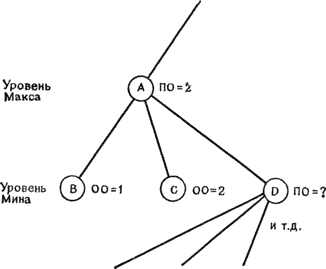
Рисунок 12.8. Часть дерева для альфа-бета-процедуры, описанного в тексте. Как только ПО в узле D опустится ниже 3, можно прекращать раскрытие узла D и его преемников.
Альфа-бета-процедура
Для выполнения альфа-бета-процедуры поиска минимакса начните с перебора дерева игры в глубину. Каждому узлу приписывается предварительная оценка (ПО) и окончательная оценка (ОО). Для листьев как ПО, так и ОО равна статической оценке. ПО во внутренних узлах Макса равна максимуму из ОО преемников этого узла, в узлах Мина — минимуму. Всякий раз, когда ПО меняется, мы проверяем, не следует ли прекратить раскрытие этого узла. (Первоначально ПО равна −∞ во внутренних узлах Макса и +∞ во внутренних узлах Мина). В узле Макса происходит отсечение всякий раз, как только ПО этого узла становится не меньше ПО какого-либо предшественника этого узла, принадлежащего Мину. Аналогично в узле Мина отсечение происходит, когда его ПО становится не больше ПО какого-либо из предшественников, принадлежащего Максу. При отсечении узла его ПО становится его ОО. Вам следует убедиться, что альфа-бета-процедура всегда выбирает тот же ход, что и обычная минимаксная процедура.
Тема. Напишите программу для игры в калах, использующую альфа-бета-процедуру. Ваша программа должна уметь играть как против человека за терминалом, так и против самой себя. Следует предусмотреть возможность изменения глубины d просмотра, числа к камней в каждой лунке, а также замены игрока, делающего первый ход. Вывод позиций и ввод ходов следует представить в наиболее удобной форме. По требованию программа должна выдавать на печать дерево ходов. Чтобы с программой было интересно играть, она должна случайным образом выбирать ход из нескольких равноправных (как обычно, эту возможность следует отключать на время отладки).
Указания исполнителю. Несмотря на многословное описание, сама программа для игры в калах довольно проста. Основную трудность составляет построение структуры данных для представления игровых деревьев и обеспечение должного порядка создания и уничтожения этих деревьев. Вам, вероятно, придется написать свои собственные программы, которые будут выделять пространство для деревьев и собирать освобождающуюся память. Требование эффективности по времени работы накладывает ограничение на глубину просмотра; учитывайте это в программах порождения дерева. Вероятно, имеет смысл обеспечить относительную независимость минимаксной процедуры от остальной части программы, с тем чтобы изменения минимаксной процедуры не влияли на всю программу.
Развитие темы. Хотя в литературе, указанной в библиографии, содержится большое число модификаций альфа-бета-процедуры, мы обсудим здесь только две из них. В первой делается попытка повысить эффективность отсечения. Работа альфа-бета-процедуры основана на том, что хорошие ходы (за обоих игроков) прекращают анализ худших ходов. Поэтому, чем раньше мы будем находить хорошие ходы, тем чаще будут отсекаться плохие. Итак, следует попытаться в первую очередь раскрывать хорошие ходы. В методе с фиксированным упорядочением непосредственные преемники узла упорядочиваются с помощью статической оценочной функций до их анализа. Первым раскрывается узел с наилучшей оценкой. Статическая оценочная функция, как мы надеемся, хорошо предсказывает окончательный результат, получаемый с помощью просмотра, следовательно, эта процедура повышает вероятность того, что сначала будут рассматриваться хорошие ходы. В узлах Мина в первую очередь следует рассматривать преемники с минимальной оценкой.
Еще одно обобщение состоит в изменении статической оценочной функции. Часто используют оценку, равную разности числа всех камней на стороне Макса (в калахе и лунках) и числа камней на стороне Мина. Можно применить любую простую линейную функцию от 14 значений для всех лунок. Наилучшую такую функцию можно выбрать при помощи турнира. Не забывайте, однако, что главным фактором, определяющим силу игрока, является, до всей видимости, глубина просмотра.
Тема 13: Поиск узоров из простых чисел
Всякий, кто изучает простые числа, бывает очарован ими и одновременно ощущает собственное бессилие. Определение простых чисел так просто и очевидно; найти очередное простое число так легко; разложение на простые сомножители — такое естественное действие. Почему же тогда простые числа столь упорно сопротивляются нашим попыткам постичь порядок и закономерности их расположения? Может быть, в них вообще нет порядка, или же мы так слепы, что не видим его?
Какой-то порядок в простых числах, несомненно, есть. Простые числа можно отсеять от составных решетом Эратосфена. Начнем с того, что 2 — простое число. Теперь выбросим все большие четные числа (делящиеся на 2). Первое из уцелевших за двойкой чисел, 3, также должно быть простым. Удалим все его кратные; останется 5. После удаления кратных пяти останется 7. Будем продолжать в том же духе; все числа, прошедшие через решето, будут простыми. Эта регулярная, хотя и медленная процедура находит все простые числа. Мы знаем, кроме того, что при n, стремящемся к бесконечности, отношение количества простых чисел к составным среди первых целых чисел приближается к ln n/n. К сожалению, этот предел чисто статистический и не помогает при нахождении простых чисел.
Оказывается, что все известные методы построения таблицы простых чисел — не что иное, как вариации унылого метода решета. Эйлер придумал формулу x2 + x + 41; для всех x от нуля до 39 эта формула дает простые числа. Однако никакая полиномиальная формула не может давать подряд бесконечный ряд простых чисел, и функция Эйлера терпит фиаско при х = 40. Другие известные функции дают длинные ряды простых чисел, но ни одна не дает сплошь простые. Исследователи проанализировали множество целочисленных функций, однако до сих пор не удалось увидеть закономерность.

Рисунок 13.1. Числа расположены по спирали против часовой стрелки.
Закономерности проявляются, когда целые числа отображаются на плоскость (или в пространство). Одно из возможных отображений показано на рис. 13.1, где числа располагаются вокруг начальной точки по спирали против часовой стрелки. На рис. 13.2 целые числа заполняют треугольник положительного квадранта. Если достаточно далеко расширить рамки этих рисунков, то станет видно, что простые числа располагаются преимущественно вдоль отдельных прямых (в основном по диагоналям) и совершенно игнорируют другие прямые. Частично этот эффект легко объясним* В обоих расположениях целые числа, попадающие на любую диагональ, даются некоторым квадратичным многочленом. Если многочлен, соответствующий какой-либо прямой, разлагается на рациональные линейные множители, то эта прямая будет содержать одни составные числа. Таким образом, простым числам волей-неволей пришлось облюбовать неприводимые прямые. Однако некоторые неприводимые многочлены изобилуют простыми числами, и изобилие это не оскудевает, несмотря на то что плотность простых чисел среди всех целых медленно стремится к нулю. Иными словами, хотя разложение многочленов объясняет в некоторой степени скученность простых чисел, все же существуют многочлены, более богатые простыми числами, чем предсказывает обычный статистический анализ.

Рисунок 13.2. Числа в треугольнике.
Тема. Напишите программу, которая отображает целые числа на плоскость некоторым регулярным образом и отмечает на рисунке места, где находятся простые числа. Выведите формулы, описывающие прямые линии на вашем рисунке, и напечатайте те из них, которые особенно изобилуют простыми числами; печатайте также долю простых чисел на этих прямых. Обеспечьте высокую эффективность ваших программ проверки целых чисел на простоту, так чтобы вам хватило времени для анализа весьма отдаленных отрезков натурального ряда.