ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5658
Скачиваний: 10

36
рованы
.
Произвольным
образом
выберем
элемент
первого
мно
-
жества
:
а
1
∈
S
1
в
качестве
его
представителя
.
Поочередно
будем
выбирать
представителей
других
множеств
:
а
2
∈
S
2,
а
3
∈
S
3
,
забо
-
тясь
о
том
,
чтобы
каждый
из
них
был
отличен
от
любого
другого
.
Если
такие
операции
будут
доведенные
до
а
n
∈
S
n
включительно
,
то
мы
получим
искомую
с
.
п
.
р
.
Может
получиться
,
что
в
ходе
постепенного
подбора
t
ша
-
гов
мы
дойдем
до
некоторого
t-
множества
S
t
(t<n),
элементы
ко
-
торого
b
1
,b
2
,...,b
t
уже
были
выбраны
представителями
других
эле
-
ментов
.
Это
еще
не
означает
,
что
с
.
п
.
р
.
не
существует
.
Будем
по
-
очередно
брать
все
те
множества
,
представителями
которых
яв
-
ляются
эти
элементы
,
и
удалять
из
них
все
элементы
,
которые
уже
являются
представителями
множеств
,
а
оставшиеся
припи
-
сывать
к
b
1
,b
2
,...,b
t
до
тех
пор
,
пока
: 1)
либо
мы
встретим
элемент
b
i1
∈
S
j1
(i
1
>t; j
1
< t),
который
не
является
еще
представителем
; 2)
ли
-
бо
мы
не
найдем
элемента
,
который
не
был
бы
представителем
.
В
этом
случае
мы
можем
быть
убеждены
,
что
с
.
п
.
р
.
не
существует
.
Если
же
имеет
место
1),
т
.
е
.
на
некотором
этапе
мы
находим
b
i1
∈
S
j1
(i
1
>t; j
1
< t),
не
являющийся
до
сих
пор
представителем
,
то
это
означает
,
что
представителем
S
j1
уже
был
выбран
другой
элемент
b
i2
(i
2
> i
1
).
Если
i
2
> t,
то
значит
b
i2
∈
S
j2
,
представителем
которого
является
b
i3
(i
3
> i
2
),
и
т
.
д
.
Таким
образом
,
возникает
по
-
следовательность
bi
1
,bi
2
,...,bim,
индексы
которой
убывают
(i
m
≤
t),
причем
в
этой
последовательности
каждый
ее
член
входит
в
мно
-
жество
,
представителем
которого
является
следующий
член
.
За
-
меняем
представителей
,
выбирая
элементы
: b
i1
для
S
j1,
b
i2
для
S
j2
,..., b
im–1
для
S
jm–1
.
Элемент
b
im
в
результате
этой
замены
осво
-
бождается
для
выбора
в
качестве
представителя
S
t
.
Итак
, S
1
,...,S
t
имеют
различных
представителей
,
и
мы
можем
следовать
тем
же
путем
,
имея
в
виду
либо
возможность
дойти
до
S
n
и
получить
полную
с
.
п
.
р
.,
либо
встретить
случай
2)
и
установить
несущест
-
вование
с
.
п
.
р
.
Заключение
о
числе
с
.
п
.
р
.
получается
из
приведенного
алго
-
ритма
как
следствие
.
Действительно
,
если
с
.
п
.
р
.
существует
,
то
это
значит
,
что
существует
также
некоторое
множество
,
каждый
элемент
которого
может
быть
выбран
в
качестве
его
представите
-

37
ля
в
с
.
п
.
р
.
Множество
,
которое
может
иметь
в
качестве
предста
-
вителя
любой
свой
элемент
,
обозначим
через
S
1
.
Выбор
предста
-
вителя
в
S
1
можно
осуществить
не
менее
,
чем
t
способами
.
Вы
-
черкнем
теперь
элемент
,
выбранный
в
качестве
представителя
для
S
1
,
из
S
2
,..., S
n
и
получим
множества
S
2
’
,..., S
n
’
,
которые
обладают
с
.
п
.
р
.
и
в
которых
наименьшее
множество
содержит
не
меньше
,
чем
t – 1
элементов
.
Продолжая
дальше
таким
же
образом
,
мы
можем
получить
не
меньше
,
чем
t(t –1)... (t – n +1)
с
.
п
.
р
.,
если
t
≥
n
и
не
меньше
,
чем
t!
с
.
п
.
р
.,
если
t < n.
Имеет
место
теорема
Кенига
,
эквивалентная
теореме
Ф
.
Холла
.
Теорема Кенига.
Если
прямоугольная
матрица
составлена
из
нулей
и
единиц
,
то
минимальное
число
линий
(
строк
либо
столб
-
цов
),
которые
содержат
все
единицы
,
равно
максимальному
числу
единиц
,
которые
могут
быть
выбраны
так
,
чтобы
никакие
две
из
них
не
лежали
на
одной
и
той
же
линии
.
Параллель
между
теоремами
Холла
и
Кенига
можно
провес
-
ти
следующим
образом
.
Пусть
даны
множества
S
1
,..., S
n
с
элемен
-
тами
a
1
,...,a
m
.
Образуем
матрицу
А
= (n
ij
),
где
а
ij
= 1,
если
а
j
∈
S
i
,
и
a
ij
= 0
в
противоположном
случае
.
Если
единицы
в
А
СОДЕРЖАТСЯ
В
КАКИХ
−ЛИБО
R
СТРОКАХ
И
S
СТОЛБЦАХ
и
r + s < n,
то
в
k = n – r
строках
,
не
входящих
в
число
покры
-
вающих
строк
,
единицы
имеются
только
в
s<n – r = k
столбцах
и
для
этих
к
множеств
отсутствует
к
различных
элементов
.
Но
если
минимальное
покрытие
линиями
содержит
r + s = n
линий
,
то
по
теореме
Кенига
имеется
n
единиц
,
из
которых
никакие
две
не
ле
-
жат
на
одной
линии
,
и
соответствующие
этим
единицам
элемен
-
ты
образуют
с
.
п
.
р
.
для
S
1
,...,S
n.
38
2
ОСНОВЫ
ТЕОРИИ
ГРАФОВ
2.1
Основные
определения
Понятие
графа
служит
для
математического
изучения
таких
ситуаций
,
когда
имеются
совокупности
объектов
,
причем
объекты
второй
группы
играют
роль
связок
,
соединяющих
пары
объектов
первой
группы
между
собой
.
Конкретно
речь
может
идти
,
напри
-
мер
,
об
отдельных
деталях
электрической
схемы
и
соединяющих
их
проводниках
,
городах
и
соединяющих
их
дорогах
,
о
людях
и
отно
-
шениях
знакомства
между
ними
,
о
числах
и
отношениях
кратности
и
т
.
д
.
Для
одной
и
той
же
пары
объектов
первой
группы
допускает
-
ся
одновременное
наличие
нескольких
связей
,
среди
которых
до
-
пускаются
как
односторонние
,
так
и
двухсторонние
;
возможны
также
связи
,
соединяющие
один
объект
с
самим
собой
.
Точное
определение
графа
L
состоит
в
том
,
что
задаются
два
множества
X
и
U (
первое
из
которых
обязательно
непустое
),
трехместный
предикат
Р
,
указывающий
,
какую
пару
элементов
первого
множества
соединяет
тот
или
иной
элемент
второго
:
L=(X,U,P).
Элементы
множества
Х
называют
вершинами
,
элементы
U
−
ребрами
,
предикат
Р
−
инцидентором
.
Высказывание
Р
(x,u,y)
читается
так
: «
ребро
u
соединяет
вершину
х
с
вершиной
у
».
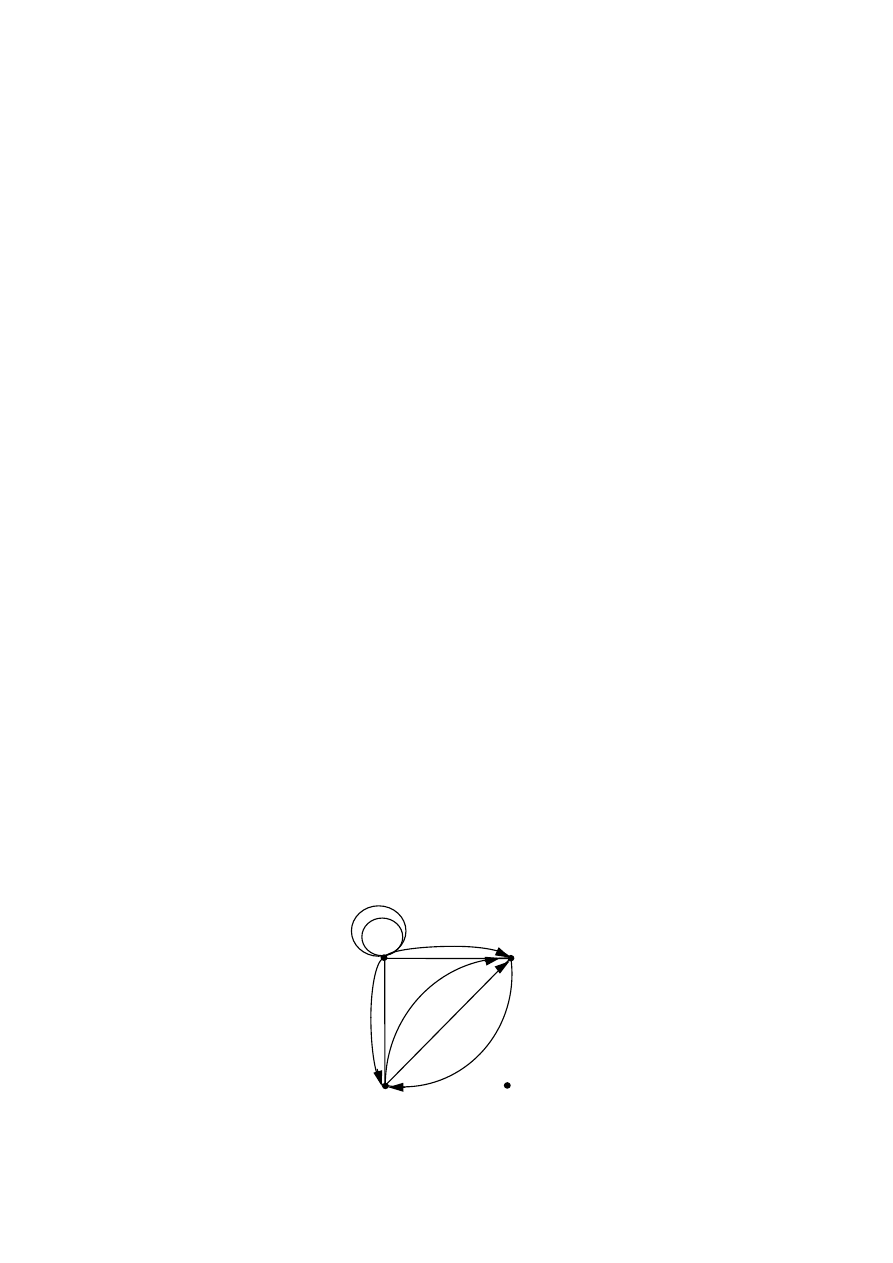
Рассмотрим
граф
,
приведенный
на
рисунке
2.1.1.
Здесь
X={a,b,c,d}, U={1,2,3,...9},
инцидентор
Р
определен
так
:
одинна
-
дцать
значений
P(a,1,a), P(a,2,a), P(a,3,b), P(a,4,b), P(b,4,a), P(a,5,c),
P(a,6,c), P(c,6,a), P(c,7,b), P(c,8,b), P(b,9,c)
−
истинны
,
а
остальные
133
ложны
.
Рис. 2.1.1
3
4
a
b
5 6 7 8
9
c
d
1
2

39
Легко
проверить
,
что
для
каждого
U
∈U
истинно
одно
и
только
одно
из
следующих
трех
высказываний
:
∃
x,y[x
≠
y
&
P(x,u,y)
&
⎤
P(y,u,x),
∃
xP(x,u,x),
∃
x,y[x
≠
y
&
P(x,u,y)
&
P(y,u,x)]. (2.1.1)
Если
высказывание
(2.1)
в
отношении
U
−
истинно
,
то
U
на
-
зывается
дугой
и
считаем
, u
∈
U
−
множество
дуг
.
Следующим
возможным
высказыванием
является
,
{
,
y
x
X
y
x
≠
∈
∃
&
P(x,u,y)
&
P(y,u,x)}. (2.1.2)
Если
истинно
(2.2),
то
u
называется
звеном
, u U
~
∈ −
множест
-
во
звеньев
.
И
последним
возможным
высказыванием
является
∃x∈X{P(x,u,x)}. (2.1.3)
В
этом
случае
u
называется
петлей
u U
∈ .
Итак
,
множество
ребер
может
быть
представлено
в
виде
U
U
U
U
∪
∪
=
~
.
Пусть
для
некоторой
тройки
элементов
x, u, y
истинно
вы
-
сказывание
P(x,u,y),
т
.
е
.
ребро
u
соединяет
вершину
х
с
вершиной
у
;
если
при
этом
еще
и
выполняется
(2.1.1),
т
.
е
.
U
u
∈
,
то
говорят
:
«
дуга
u
идет
из
вершины
х
в
вершину
у
»;
если
выполняется
(2.1.2),
т
.
е
.
U
u
~
∈ ,
то
говорят
: «
звено
xyu
соединяет
вершины
х
и
у
»;
если
выполняется
(2.1.3),
т
.
е
.
U
u
∈
(
и
,
значит
,
х
=
у
),
то
гово
-
рят
: «u
есть
петля
при
вершине
х
».
Для
графа
,
изображенного
на
рисунке
2.1.1,
имеем
:
},
9
,
8
,
7
,
5
,
3
{
=
U
}
6
,
4
{
~ =
U
и
}
2
,
1
{
=
U
.
Две
вершины
х
и
у
называются
смежными
,
если
существует
по
крайней
мере
одно
соединяющее
их
ребро
;
в
частности
,
вер
-
шина
смежна
сама
с
собой
в
том
и
только
том
случае
,
когда
при
ней
имеется
хотя
бы
одна
петля
.
С
помощью
инцидентора
Р
определим
еще
три
двухместных
предиката
)}
,
,
(
{
)
,
(
z
u
x
P
X
z
u
x
J
∈
∃
⇔
+
; (2.1.4)
)}
,
,
(
{
)
,
(
x
u
z
P
X
z
u
x
J
∈
∃
⇔
−
; (2.1.5)
)
,
,
(
)
,
(
0
x
u
x
P
u
x
J
⇔
. (2.1.6)

40
2.2
Задание
графов
с
помощью
матриц
Конкретный
граф
полностью
задается
множествами
X, U
и
инцидентором
Р
.
В
свою
очередь
инцидентор
Р
,
будучи
трехме
-
стным
предикатом
,
требует
трехмерной
таблицы
истинности
−
трехмерной
матрицы
с
U
X
⋅
2
элементами
(
А
−
мощность
мно
-
жества
А
).
Если
использовать
три
двухместных
предиката
0
,
ЏI
I
I
−
+
,
то
можно
обойтись
тремя
двухмерными
таблицами
.
Однако
все
эти
способы
задания
графа
в
виде
матриц
неэф
-
фективны
.
Наиболее
эффективным
является
задание
графа
с
помощью
двухмерной
матрицы инциденций
.
Матрицей инциденций
графа
называется
прямоугольная
таблица
;
,
1
;
,
1
m
j
n
a
A
ij
=
=
=
элементы которой
j
i
a
,
принадле-
жат свободному полукольцу К с нулем 0, порожденному четырь-
мя образующими
,
,
,
,
θ
ζ
η
ξ
и определяются по графу L следую-
щим образом:
если
j
U
− дуга, исходящая из вершины
i
x
, то
ξ
=
ij
a
;
если
j
U
− дуга, заходящая в
i
x
, то
η
=
ij
a
;
если
j
U
− петля при вершине
i
x
, то
ζ
=
ij
a
;
если
j
U
− звено, инцидентное
i
x
, то
θ
=
ij
a
;
и если ребро
j
U
неинцидентно вершине
i
x
, то
0
=
ij
a
.
Для рассматриваемого графа (рис. 2.1.1) матрица инциден-
ций имеет вид:
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
η
ξ
ξ
θ
η
ξ
η
η
θ
η
θ
ξ
θ
ξ
η
η
d
c
b
a
A
=
u
1
u
2
u
3
u
4
u
5
u
6
u
7
u
8
u
9
Ясно, что каждый столбец матрицы инциденций содержит
либо один, либо два ненулевых элемента, причем в первом случае
это обязательно
ζ, а во втором ξ и η или θ и θ.