ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5663
Скачиваний: 10

46
кающихся подмножества
''
и
'
X
X
так, чтобы две вершины одно-
го и того же подмножества не были бы смежны (т.е. раскрасить
все вершины графа L(X,U;P) двумя цветами, чтобы смежные
вершины имели разные цвета).
Очевидно, что граф является бихроматическим тогда и
только тогда, когда он не содержит петель, а его скелет есть граф
Кёнига.
Венгерский алгоритм
Венгерский алгоритм (Эгервари 1931, Кун 1953) предназна-
чен для решения так называемых
задач
о
назначении
, которые в
свою очередь в своем простейшем виде сводятся к нахождению
наибольшего паросочетания у заданного графа Кёнига.
Проиллюстрируем венгерский алгоритм на следующем при-
мере.
Пусть имеется девять иностранных групп туристов T
1
,…,T
9,
причем гости группы Т
1
говорят на языке А, гости Т
2
– на Б,Т
3
–
на В, Т
4
– на А, Т
5
– на Б, Т
6
– на Г, Т
7
– на Е, Т
8
– на Г,Т
9
– на Д; в
свою очередь бюро «Интурист» располагает в данный момент де-
сятью свободными переводчиками П
1
,…, П
10
, владеющими таки-
ми иностранными языками: П
1
– языком (А,В); П
2
– (А,Г); П
3
–
(А); П
4
– (Б,В,Е); П
5
– (А,В); П
6
– (А), П
7
– (Г,Д); П
8
– (Б,Д); П
9
–
(Б,Г,Е); П
10
– (А,Б). Необходимо взаимно однозначно прикрепить
переводчиков к группам, чтобы в первую очередь было обслуже-
но, возможно большее число групп.
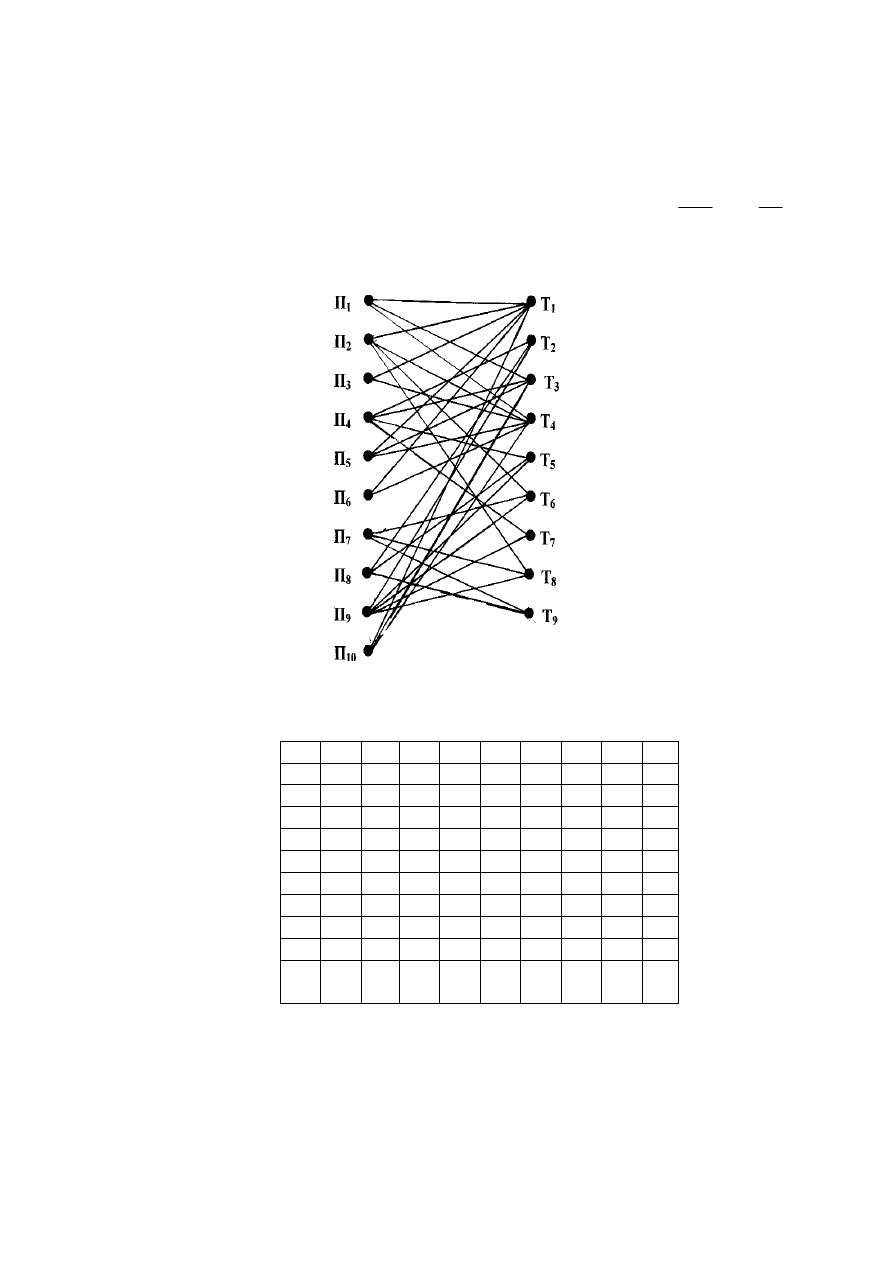
Построим граф Кёнига
)
,
(
2
,
1
U
X
X
L
=
(рисунок 2.4.1), в ко-
тором вершинам множества X
1
соответствуют переводчики
П
1
,
П
2
,…,
П
10
, вершинам X
2
– группы туристов
Т
1
,
Т
2
,…,
Т
9.
Смеж-
ность вершины
П
i
∈X
1
с вершиной
Т
i
∈X
2
означает владение i-го
переводчика языком j-ой группы. Требуется найти в L паросоче-
тание с наибольшим количеством
π(L) ребер.
Теорема Кёнига
−Орэ позволяет вычислить наибольшее
значение для
π(L):
π(L)= ⏐
1
X
⏐
– max(
⎢A ⎢− ⎢ΔA⏐).
47
Здесь
Δ
A – подмножество вершин множества
2
X , смежных с
вершинами из A
⊆
1
X .
Для решения данной задачи представим граф
)
,
2
1
,
(
U
X
X
L
=
его матрицей смежности B=(b
ij
),
9
,
1
;
10
,
1
=
=
j
i
(рисунок 2.4.2).
Рисунок 2.4.1
B =
Рисунок 2.4.2
Строки матрицы B соответствуют элементам множества
1
X
(переводчики), столбцы – элементам множества
2
X (туристы).
Т1 Т2 Т3 Т4 Т5 Т6 Т7 Т8 Т9
П1
1
1
1
П2
1 1 1 1
П3
1
1
П4
1
1
1
1
П5
1
1
1
П6
1
1
П7
1
1
1
П8
1
1
1
П9
1 1 1 1 1
П1
0
1
1
1

48
Элементы
{ }
0
,
1
=
ij
b
;
ij
b = 1– если I-й переводчик может
обслуживать j-ю группу туристов, b
ij
= 0 – в противном случае.
Алгоритм решения состоит в следующем. Пусть некото-
рое паросочетание K=(Y
1
, Y
2
, V) уже построено (в начальный мо-
мент это пустое паросочетание, V=
∅). Ребра графа L , принадле-
жащие V назовем «сильными», а ребра из U\V – «слабыми». Вер-
шину, инцидентную
сильному
ребру будем называть
насыщенной
,
а вершину, не инцидентную сильному ребру, –
ненасыщенной
.
Под «
чередующейся
цепью
» будем понимать простую цепь, в ко-
торой слабые рёбра строго чередуются с сильными; такую цепь
назовем
тонкой
. Примем, что её длина отрицательна, если на-
чальная и конечная вершины – обе ненасыщенные.
Ясно, что при наличии у графа L с заданным паросочетани-
ем K хотя бы одной тонкой чередующейся цепи Q можно вместо
К
построить новое паросочетание
К
’, содержащее на одно ребро
больше. Для этого надо все
слабые
ребра цепи Q сделать
силь
-
ными
, а
сильные
– слабыми, не трогая рёбер вне Q. Иначе говоря,
надо удалить из множества V все те рёбра, которые принадлежат
цепи Q, и к остатку добавить рёбра Q, принадлежащие U\V. В
свою очередь, если у графа L с паросочетанием К’ опять есть
тонкая чередующаяся цепь, то аналогично предыдущему можно
получить паросочетание
К
’’, имеющее уже на два ребра больше
исходного.
Оказывается, что если на каком-то этапе тонких чередую-
щихся цепей больше нет, то полученное паросочетание
К
*
– наи-
большее, т.е. содержит ровно
π(L) ребер.
Процедура поиска тонкой чередующейся цепи в графе с за-
данным паросочетанием состоит в следующем: выбираем в X
1
любую ненасыщенную вершину и строим из нее чередующуюся
цепь, отмечая штрихом пройденные рёбра и не выбирая их в
дальнейшем. Попав в уже пройденную вершину или такую вер-
шину из
Х
1
, которая не инцидентна ни одному еще не пройденно-
му слабому ребру, возвращаемся на один шаг, отмечаем ребро
вторым штрихом и пытаемся проложить чередующуюся цепь
иначе, и т.д. В результате процесс либо оборвется в ненасыщен-
ной вершине множества
Х
2
, и мы получим искомую цепь (она со-

49
стоит из рёбер, отмеченных ровно одним штрихом), либо этот
процесс приведёт нас в исходную вершину, и тогда надо начать
аналогичный поиск с другой ненасыщенной вершины множества
Х
1
.
В нашем конкретном примере всё решение выглядит сле-
дующим образом.
1. Задаём произвольно паросочетание K={(П
3
Т
1
),( П
2
Т
4
)}.
2. Фиксируем насыщенные вершины – П
3
, П
2
и Т
1
,Т
4
.
3. Строим тонкую чередующуюся цепь Q: П
1
– Т
1
– П
3
– Т
4
–
П
2
–Т
8
, которая начинается и заканчивается в ненасыщенных
вершинах П
1
и Т
8
и содержит сильные рёбра (П
3
–Т
1
) и (П
2
–Т
4
).
4. Переименуем рёбра построенной тонкой цепи: теперь
рёбра (П
3
– Т
1
) и (П
2
– Т
4
) – слабые, а рёбра (П
1
–Т
1
), (П
3
–Т
4
), (П
2
– Т
8
) соответственно стали сильными, вершины П
1 ,
Т
8
– насы-
щенные. Новое паросочетание K’ содержит уже три ребра.
5. Находим в графе новые ненасыщенные вершины Т
3
и П
7
,
которые смежны насыщенным концевым вершинам построенной
тонкой цепи
П
1
–Т
1
–П
3
–Т
4
– П
2
–Т
8
.
6. Строим новую тонкую чередующуюся цепь Q: Т
3
– П
1
–Т
1
– П
3
– Т
4
– П
2
– Т
8
– П
7
, которая содержит сильные рёбра (П
1
–
Т
1
), (П
3
–Т
4
), (П
2
–Т
8
).
7. Переименуем рёбра построенной тонкой чередующейся
цепи: теперь рёбра (П
1
–Т
1
), (П
3
–Т
4
), (П
2
–Т
8
) – слабые, а рёбра
(Т
3
– П
1
), (Т
1
–П
3
), (Т
4
– П
2
), (Т
8
– П
7
) – сильные. Новое паросоче-
тание K’’ содержит уже четыре ребра.
8. Присоединим к построенной тонкой чередующейся цепи
Т
3
– П
1
– Т
1
–П
3
–Т
4
– П
2
–Т
8
– П
7
ещё два ребра: (Т
3
– П
4
) и (П
7
–
Т
6
) и над новой чередующейся цепью Q = П
4
– Т
3
–П
1
– Т
1
–П
3
–
Т
4
– П
2
–Т
8
– П
7
– Т
6
выполним преобразование, аналогичное то-
му, которое описано в п.п. 4,7 , увеличив таким образом паросо-
четание K’’ ещё на одно ребро. Новое паросочетание K
ν
вклю-
чает сильные рёбра – (П
4 ,
Т
3
), (П
1
, Т
1
), (П
3
, Т
4
), (П
2 ,
Т
8
), (П
7
, Т
6
).
Увеличить длину построенной цепи Q, проходящей через
вершины П
4 ,
Т
3
, П
1
, Т
1
, П
3
, Т
4
, П
2
, Т
8
, П
7
, Т
6
, нельзя, так как
среди ненасыщенных вершин из множества X\V, принадлежащих

50
разным подмножествам (X
1
, X
2
), нет инцидентных концевым вер-
шинам цепи Q.
Увеличить построенное паросочетание K
ν
можно добавле-
нием к нему цепей длины, равной 1, т.е. рёбер ( П
8
, Т
9
) и ( П
9
, Т
5
)
или ( П
9
, Т
7
) и (П
8
, Т
9
). Тогда количество рёбер
π(L) паросочета-
ния K
ν
станет равно 7.
Q = П
4
, Т
3
, П
1
, Т
1
, П
3
, Т
4
, П
2
, Т
8
, П
7
, Т
6
, П
9
, Т
5
, П
8
, Т
2
.
Т1+ Т2* Т3+ Т4+ Т5+ Т6* Т7 Т8+ Т9
П1+ 1+
1–
1
П2+ 1 1– 1 1+
П3+ 1–
1
+
П4* 1
1+
1
1
П5
1
1 1
П6
1
1
П7+ 1+
1–
1
П8+ 1–
1+
1
П9+ 1
1–
1+
1
1
П10 1 1
Рисунок 2.4.3
На рисунке 2.4.3 показана матрица смежности B графа L, где
знаком ‘+’ помечены насыщенные вершины графа и элементы b
ij ,
соответствующие сильному ребру, т.е. ребру паросочетания K
ν
,
значком ‘*’ помечены концевые вершины чередующейся цепи Q,
знаком ‘–’ помечены элементы b
ij
, соответствующие слабому
ребру, т.е. ребру, которое не входит в паросочетания K
ν
.
Из матрицы
видно, что увеличить построенное паросочета-
ние нельзя так как оставшиеся ненасыщенные вершины инци-
дентны разным рёбрам.
Однако согласно теореме Кёнига–Холла для данного графа
π(L) = 8. Действительно, если мы в построенной тонкой чере-
дующейся цепи Q ребро (П
4 ,
Т
3
) заменим ребром (П
5 ,
Т
3
), то
сможем построить другую чередующуюся цепь Q, которая про-
ходит через вершины П
5
, Т
3
, П
1
, Т
1
, П
6
, Т
4
, П
2
, Т
6
, П
7
, Т
8
, П
9
,
Т
5
.