ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5659
Скачиваний: 10

41
Для описания характера связи между парами вершин графа
вводится матрица соседства вершин:
B=A*
T
A .
Например, для рассматриваемого в качестве примера графа
имеем:
.
;
2
2
2
2
1
2
1
12
2
2
2
2
2
2
2
1
2
2
1
1
11
θ
η
ξ
θ
ξ
ζ
θ
ξ
θ
ξ
ζ
ζ
+
=
=
+
+
=
+
+
+
+
+
=
=
∑
∑
=
=
g
k
k
k
g
k
k
k
a
a
b
a
a
b
В общем случае элемент матрицы имеет вид:
),
(
)
;
(
~
)
;
(
)
;
(
;
)
(
~
)
(
)
(
)
(
2
2
2
0
2
2
j
i
x
x
S
x
x
S
x
x
S
b
x
S
x
S
x
S
x
S
b
j
i
j
i
j
i
ij
i
i
i
i
ii
≠
+
+
=
+
+
+
=
−
+
−
+
θ
ηξ
ξη
θ
ζ
η
ξ
где
)
(
i
x
S
+
− количество дуг, исходящих из вершины ;
i
x
)
(
i
x
S
−
− количество дуг, заходящих в ;
i
x
)
(
0
i
x
S
− количество петель при вершине ;
i
x
)
(
~
i
x
S
− количество звеньев, инцидентных ;
i
x
)
;
(
j
i
x
x
S
+
− количество дуг, идущих из
i
x в
;
j
x
)
;
(
j
i
x
x
S
−
− количество дуг, идущих из
j
x в ;
i
x
)
;
(
~
j
i
x
x
S
− количество звеньев, соединяющих
i
x и
.
j
x
Число
)
(
~
)
(
)
(
)
(
0
x
S
x
S
x
S
x
S
Sx
+
+
+
=
−
+
называется степенью,
а
)
(
)
(
)
(
0
x
S
x
S
x
V
+
=
− валентностью вершины Х.
При переходе от матрицы инциденции к матрице соседства
теряется индивидуализация ребер графа, иначе говоря, матрица В
определяет граф с точностью до перенумерования ребер.
Часто используется также так называемая матрица смежности
)
,
1
,
(
n
j
i
r
R
ij
=
=
, где
⎪⎩
⎪
⎨
⎧
=
≠
=
.
,
)
(
,
,
2
0
j
i
x
S
j
i
b
r
j
ij
ij
ζ
Значительно
более
редко
используется
матрица соседства
ребер
графа
.
A
A
H
T
⋅
=

42
Во
многих
случаях
,
когда
требуется
лишь
частичная
инфор
-
мация
о
графе
либо
граф
заведомо
имеет
специальный
вид
,
мат
-
рицы
A, B, R
и
Н
удается
значительно
упростить
,
переходя
от
по
-
лукольца
К
к
новому
полукольцу
путем
наложения
тех
или
иных
определяющих
соотношений
на
образующие
ξ, η, ζ, θ.
2.3
Основные
типы
графов
Пусть
имеется
граф
L=(X,U,P),
где
U
U
U
U
∪
∪
=
~
.
Если
∅
=
U
~
−
граф
называется
орграфом
(
ориентированным
графом
);
при
∅
=
U
−
неорграф
(
неориентированный
граф
);
если
∅
=
U
−
то
добавляют
слова
«
без
петель
»;
и
∅
=
U
−
пустой граф
.
При
изучении
таких
свойств
графа
=
L
~
(X,U;P),
которые
за
-
висят
от
направления
его
дуг
,
удобно
пользоваться
предикатом
,
называемым
полуинцидентором:
.
)
,
,
(
)
,
,
(
)
,
,
(
~
x
u
y
P
y
u
x
P
y
u
x
P
∨
⇔
О
неорграфе
)
~
;
,
(
~
P
U
X
L
=
говорят
,
что
он
получен
из
графа
)
;
,
(
P
U
X
L
=
дезориентацией
дуг
.
Униграфом
называется
граф
,
в
котором
вершины
могут
быть
соединены
не
более
,
чем
одним
ребром
,
то
есть
такой
что
}
)
,
,
(
~
&
)
,
,
(
~
{
,
,
v
u
y
v
x
P
y
u
x
P
y
x
v
u
=
⇒
∀
∀
Мультиграф –
это
граф
,
не
являющийся
униграфом
,
т
.
е
.
р
≥
2.
Р-граф –
это
мультиграф
,
в
котором
никакая
пара
вершин
не
соединена
более
чем
р
рёбрами
.
0-граф –
это
пустой
граф
(
все
вершины
между
собой
не
связаны
).
1-граф –
это
униграф
(
вершины
связаны
не
более
чем
од
-
ним
ребром
).
Граф
называется
полным
,
если
содержит
все
ребра
,
возмож
-
ные
при
принадлежности
графа
данному
классу
и
при
неизмен
-
ном
множестве
вершин
.
Например
,
в
случае
Р
-
графа
полнота
оз
-
начает
,
что
при
каждой
вершине
имеется
ровно
р
петель
,
а
каждая
пара
различных
вершин
соединена
ровно
р
ребрами
.
Граф
общего
вида
,
в
котором
две
различные
вершины
всегда
смежны
,
называется
плотным
.
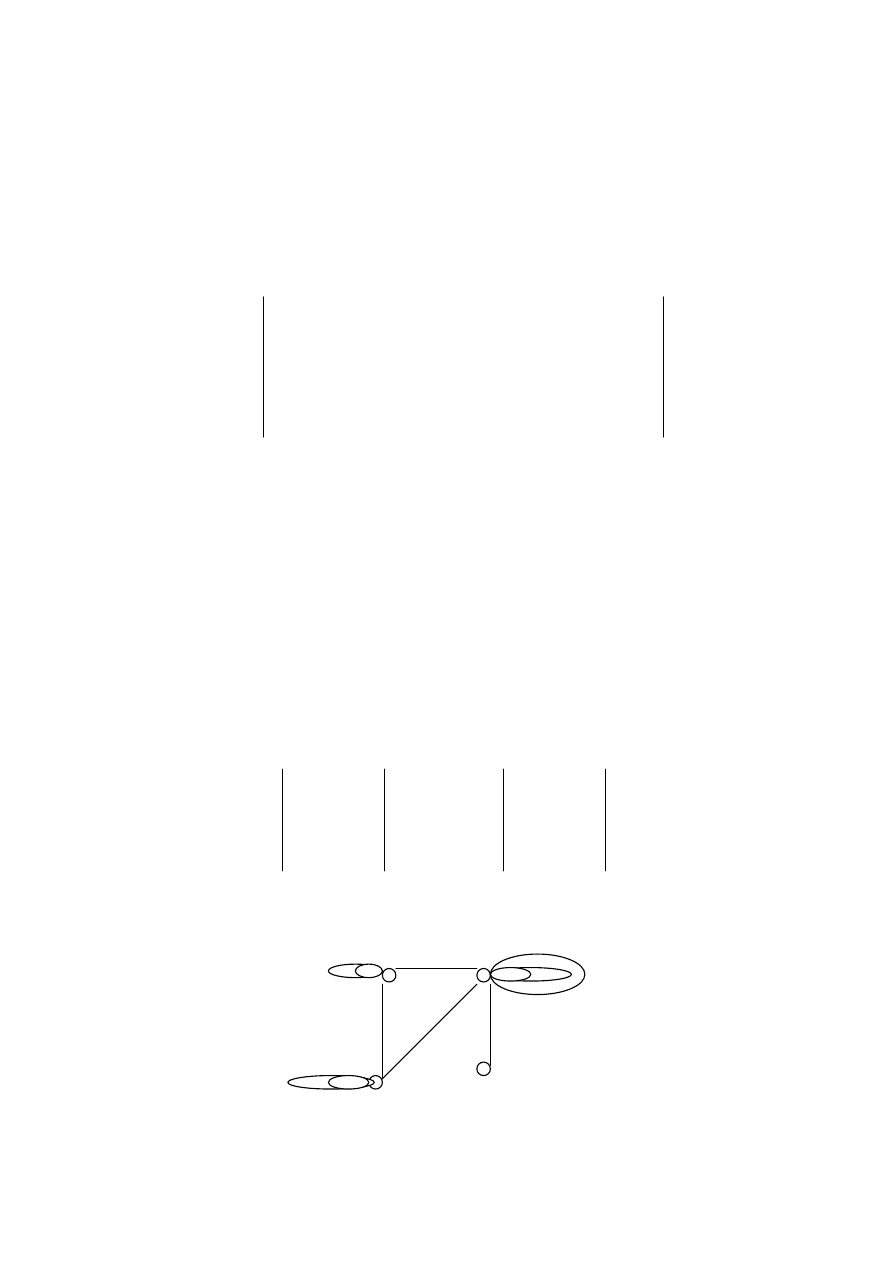
43
2
4
1
3
2.4
Обыкновенные
графы
.
Графы
Кенига
.
Графы
Бержа
Особо
важную
роль
в
теории
графов
и
ее
приложениях
иг
-
рают
неориентированные
униграфы
без
петель
,
называемые
в
дальнейшем
для
краткости
обыкновенными.
Матрица
соседства
обыкновенного
графа
имеет
вид
:
2
2
2
2
1
2
4
2
2
2
2
1
2
2
2
1
2
2
1
2
1
)
(
~
...
)
(
~
)
(
~
....
..........
...
..
..........
.
..........
)
(
~
...
)
(
~
)
(
~
)
(
~
...
)
(
~
)
(
~
θ
θ
θ
θ
θ
θ
θ
θ
θ
n
n
n
x
S
x
x
S
x
x
S
x
x
S
x
S
x
x
S
x
x
S
x
x
S
x
S
B
=
,
где
∑
≠
=
=
n
i
j
j
j
i
i
x
x
S
x
S
,
1
),
;
(
~
)
(
и
при
i
≠j.
S(x
i
;x
j
)=S(x
j
;x
i
)=
⎩
⎨
⎧
0
1
(1 –
если
x
i
и
x
j
смежны
, 0 –
в
противном
случае
).
Информация
об
обыкновенном
графе
не
будет
потеряна
,
ес
-
ли
на
полукольцо
К
будет
наложено
соотношение
θ
2
=1.
Также
без
потери
информации
о
графе
вместо
матрицы
В
можно
рассматри
-
вать
матрицу
смежности
R.
Например
,
для
графа
,
изображенного
на
рисунке
2.4
имеем
:
Матрица-соседства Матрица-смежности
Рисунок 2.4
1
1
0
0
1
3
1
1
0
1
2
1
0
1
1
2
=
B
0
1
0
0
1
0
1
1
0
1
0
1
0
1
1
0
=
R

44
Обыкновенный
граф
обозначают
(X,U),
подчеркивая
,
что
его
инцидентор
полностью
определяется
заданием
множеств
X
и
U,
так
как
&
~
~
)
,
,
(
y
x
U
y
u
x
P
=
↔
u
∈U.
Обыкновенный
граф
называется
полным
(
или
плотным
,
что
в
данном
случае
одно
и
то
же
)
и
обозначается
F
n
,
если
всякие
две
различные
его
вершины
смежны
.
Пустой
обыкновенный
граф
обозначается
E
n
.
Часто
при
исследовании
графа
общего
вида
не
требуется
полная
информация
о
графе
,
а
необходимо
лишь
знать
какие
па
-
ры
его
различных
вершин
смежны
,
а
какие
нет
;
носителем
такой
информации
является
скелет
графа
,
т
.
е
.
обыкновенный
граф
)
~
,
(
~
u
x
L
=
с
прежним
множеством
вершин
Х
и
новым
множеством
ребер
ˆ ,
U
ˆ
,
,
&
&
[ ( , , )].
x y
U
x y
X
x
y
u
U P x u y
∈ ↔
∈
≠
∃ ∈
Чтобы
из
матрицы
смежности
исходного
графа
L
над
сво
-
бодным
полукольцом
К
получить
матрицу
смежности
его
скелета
L ,
достаточно
на
образующие
полукольца
наложить
соотношение
ξη=ηξ=θ
2
;
ζ
2
=0; 2
θ
2
=
θ
2
;
θ
2
=1.
Так
граф
,
изображенный
на
рисунке
2.1.1,
имеем
скелет
:
Произвольный
граф
L
является
плотным
тогда
и
только
то
-
гда
,
когда
его
скелет
ˆ
L –
полный
.
Графы Кёнига
Обыкновенный
граф
L=(X,U)
называется
графом Кёнига,
если
множество
его
вершин
X
можно
представить
в
виде
двух
не
-
пересекающихся
подмножеств
Х
’
и
Х
’’
так
,
чтобы
никакие
вер
-
шины
одного
и
того
же
подмножества
не
были
смежны
,
т
.
е
.
X=X
’
∪X
’’
; X
’
∩X
’’
=
∅
и
ˆ
0
1
1
0
1
0
1
0
1
1
0
0
0
0
0
0
L
R
⎛
⎞
⎜
⎟
⎜
⎟
=
⎜
⎟
⎜
⎟
⎝
⎠
a
b
c
d
ˆ
L

45
)].
&
(
)
&
(
[
,
'
''
''
'
X
y
X
x
X
y
X
x
U
y
x
X
y
x
∈
∈
∨
∈
∈
⇒
∈
∈
∀
Часто
граф
Кёнига
записывают
в
виде
(X
’
,X
’’
,U).
M
атрица
смежности
графа
Кёнига
полностью
определяется
своей
прямоугольной
подматрицей
,
строки
которой
отвечают
вершинам
множества
X
’
,
а
столбцы
− X
’’
.
Граф
Кёнига
K
m
=(X,Y,W),
в
котором
⎪X⎪=⎪Y⎪=⎪W⎪=m≥1
и
никакие
два
ребра
не
смежны
,
называется
паросочеранием.
Ото
-
бражение
Δ,
которое
каждой
вершине
множества
X
относит
вер
-
шину
множества
y
здесь
является
взаимно
однозначным
соответ
-
ствием
между
этими
множествами
.
Одной
из
важных
в
прикладном
отношении
задач
теории
графов
является
задача
нахождения
наибольшего
паросочетания
,
которая
формулируется
следующим
образом
:
для
данного
графа
L
найти
наибольшее
натуральное
число
m=
π
(L),
при
котором
су
-
ществует
паросочетание
K
m
,
являющееся
частью
L.
Если
)
,'
'
,'
(
W
X
X
L
=
)
−
граф Кёнига, то под его паросочетанием пони-
мается часть
)
'
,'
'
,'
(
W
Y
Y
m
K
=
,
удовлетворяющая условию
''
''
&
'
'
X
Y
X
Y
∈
∈
. Найти
π(L) это значит выяснить, какое наи-
большее количество вершин множества
'
X
можно взаимно одно-
значно отобразить в
''
X
при помощи рёбер из W.
Теорема
Кёнига
-
Холла
: Все множество
'
X
графа Кёнига
(X
’
,X
’’
,U) можно взаимно однозначно отобразить в
''
X
при помо-
щи рёбер U тогда и только тогда, когда
∀A
⊆
'
X
(
⎢
Δ
A
⎢
≥
⎢A ⎢).
Здесь
Δ
A
− подмножество вершин множества
''
X
, смежных
с вершинами из
А
.
Свойством, лежащим в основе определения графа Кёнига,
может обладать любой, не только обыкновенный граф. Именно,
граф L(X,U;P) называется
бихроматическим
(или
двудольным
),
если множество X его вершин можно разбить на два непересе-