ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10272
Скачиваний: 94
16
столбца.
Пусть
}
...,
,
,
{
2
1
n
x
x
x
X
=
.
Тогда
матрица
отношения
X
X
R
×
⊆
имеет
n
строк и
n
столбцов, а ее элемент
ij
r
определяется по
правилу:
⎪⎩
⎪
⎨
⎧
=
∉
∈
=
.
,...,
2
,
1
,
,
)
,
(
,
0
,
)
,
(
,
1
n
j
i
R
y
x
если
R
y
x
если
r
j
i
j
i
j
i
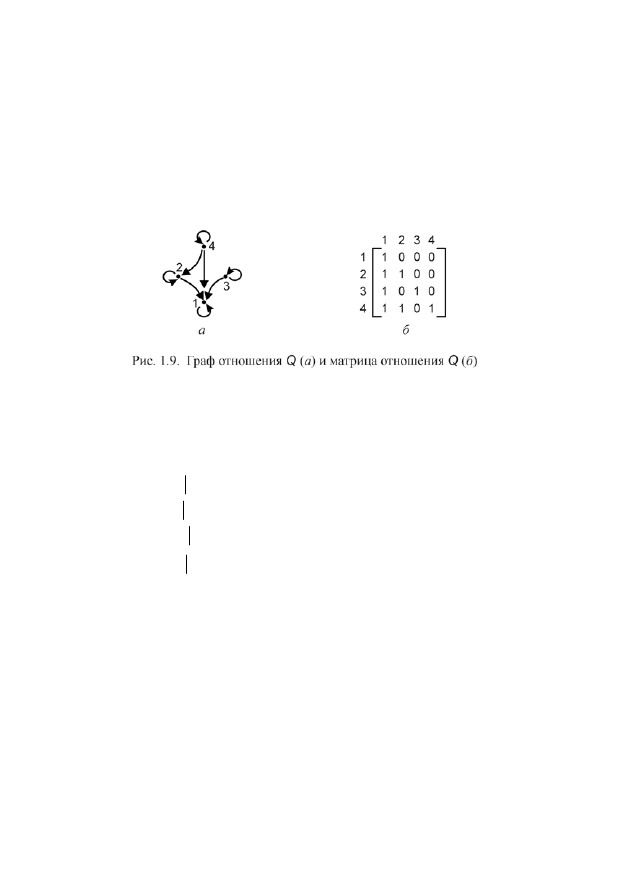
На рис.1.9, б приведена матрица отношения
Q
примера 2.
1.2.4. Свойства бинарных отношений
Бинарные отношения делятся на типы в зависимости от свойств, кото-
рыми они обладают. Рассмотрим следующие отношения на множестве
:
}
7
,
6
,
5
,
4
,
3
,
2
,
1
{
=
X
;
}
,
,
)
,
{(
y
x
X
y
x
y
x
G
>
∈
=
;
}
,
,
)
,
{(
y
x
X
y
x
y
x
L
≤
∈
=
)
(
,
,
)
,
{(
y
x
X
y
x
y
x
M
−
∈
=
делится на
;
}
3
.
}
20
,
,
)
,
{(
2
2
≤
+
∈
=
y
x
X
y
x
y
x
K
Отношение
R
на множестве
Х
называется рефлексивным, если для всех
X
x
∈
выполняется условие
R
x
x
∈
)
,
(
. Среди приведенных выше отношений
рефлексивными являются отношение
L
(т.к. неравенство
x
x
≤
справедливо
при всех
X
x
∈
) и отношение
М
(т.к. разность
0
=
− x
x
делится на 3, значит,
пара
)
,
(
x
x
принадлежит отношению
М
при всех
X
x
∈
).
Отношение
R
на множестве
Х
называется антирефлексивным, если
условие
R
x
x
∈
)
,
(
не выполняется ни при одном
X
x
∈
. Примером антире-
флексивного отношения является отношение
G
(неравенство
x
x
>
не выпол-
няется ни при каких значениях
х
, следовательно, ни одна пара
)
,
(
x
x
не при-
надлежит отношению
G
). Отметим, что отношение
К
не является рефлексив-

17
ным
)
)
5
,
5
(
20
5
5
(
2
2
K
∉
⇒
>
+
и не является антирефлексивным
)
)
1
,
1
(
20
1
1
(
2
2
K
∈
⇒
≤
+
.
Отношение
R
на множестве
Х
называется симметричным, если из усло-
вия
R
y
x
∈
)
,
(
следует
R
x
y
∈
)
,
(
. Симметричными являются отношения
М
(если
y
x
−
делится на 3, то и
x
y
−
делится на 3) и
К
(если
20
2
2
≤
+ y
x
, то
и
20
2
2
≤
+ x
y
).
Отношение
R
на множестве
Х
называется несимметричным, если для
любых
X
y
x
∈
,
из условия
R
y
x
∈
)
,
(
следует
R
x
y
∉
)
,
(
. Несимметричным
является отношение
G
, т.к. условия
y
x
<
и
x
y
<
не могут выполняться од-
новременно (только одна из пар
)
,
(
y
x
или
)
,
(
x
y
принадлежит отношению
G
).
Отношение
R
на множестве
Х
называется антисимметричным, если
для любых
X
y
x
∈
,
из условия
R
y
x
∈
)
,
(
и
R
x
y
∈
)
,
(
следует
y
x
=
. Ан-
тисимметричным является отношение
L
, т.к. из одновременного выполнения
y
x
≤
и
x
y
≤
следует
y
x
=
.
Отношение
R
на множестве
Х
называется транзитивным, если для лю-
бых
R
z
y
x
∈
,
,
из одновременного выполнения условий
R
y
x
∈
)
,
(
и
R
z
y
∈
)
,
(
следует
R
z
x
∈
)
,
(
. Отношения
G, L, M
являются транзитивными,
а отношение
К
нетранзитивно: если
,
4
,
2
,
3
=
=
=
z
y
x
то
20
2
3
2
2
≤
+
и
20
4
2
2
2
≤
+
, но
20
4
3
2
2
≥
+
, то есть выполняются условия
K
y
x
∈
)
,
(
и
K
z
y
∈
)
,
(
, но
K
z
x
∉
)
,
(
.
1.2.5. Отношения эквивалентности
Рассмотрим три отношения:
M, S, H
. Отношение
М
описано в 1.2.4. От-
ношение
S
введем на множестве
X
всех треугольников следующим образом:
этому отношению принадлежат пары треугольников такие, что площадь тре-
угольника
x
равна площади треугольника
y
.
Отношение
Н
действует на множестве жителей г. Томска и содержит па-
ры
)
,
(
y
x
такие, что
х
и
у
носят шляпы одинакового размера.
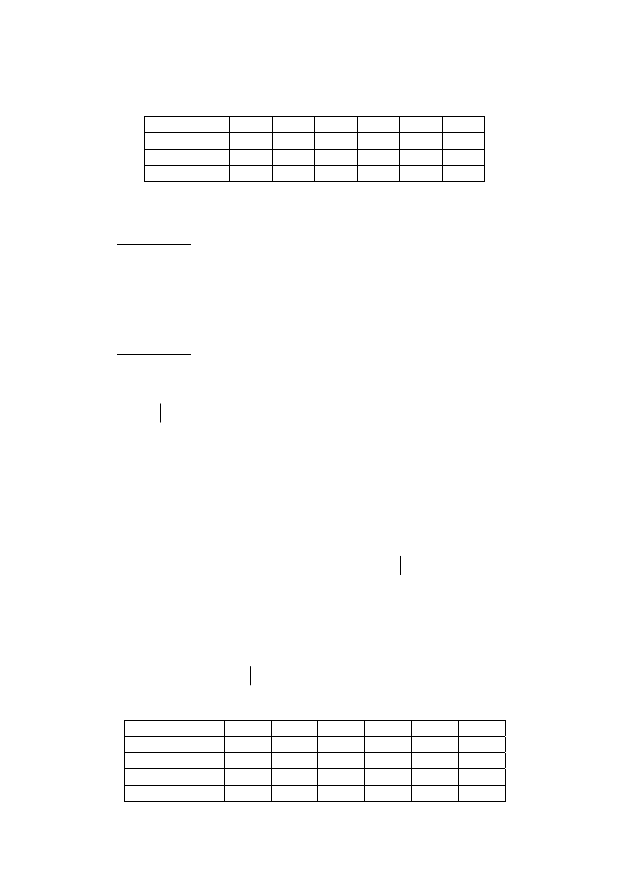
Свойства этих трех отношений приведены в таблице 1.2, где
Р
означает
рефлексивность,
АР
– антирефлексивность,
С
– симметричность,
АС
- анти-
симметричность,
НС
– несимметричность,
Т
– транзитивность отношения. В
качестве упражнения проверьте правильность заполнения таблицы, пользуясь
определениями свойств бинарных отношений.
18
Таблица 1.2
Свойства отношений
Отношение
Р
АР
С
АС
НС
Т
М
+ - + - - +
S
+ - + - - +
H
+ - + - - +
Мы видим, что отношения обладают одинаковыми свойствами, поэтому
их относят к одному типу.
Определение. Отношение
R
на множестве
Х
называется отношением эк-
вивалентности, если оно обладает свойствами рефлексивности, симметрич-
ности, транзитивности.
Таким образом, отношения
M, S, H
являются отношениями эквивалент-
ности на соответствующих множествах Х. Важной особенностью отношений
эквивалентности является то, что они разбивают все множество Х на непересе-
кающиеся подмножества – классы эквивалентности.
Определение. Классом эквивалентности, порожденным элементом
X
x
∈
, называется подмножество
]
[x
множества
Х
, для элементов которого
выполняется условие
X
y
R
y
x
∈
∈ ,
)
,
(
. Таким образом, класс эквивалентно-
сти
}
)
,
(
,
{
]
[
R
y
x
X
y
y
x
∈
∈
=
.
Так, отношение
М
разбивает множество
}
7
,
6
,
5
,
4
,
3
,
2
,
1
{
=
X
на три клас-
са эквивалентности:
}
6
,
3
{
]
3
[
},
5
,
2
{
]
2
[
},
7
,
4
,
1
{
]
1
[
=
=
=
. Класс, порожденный
элементом 4, совпадает с классом [1]; [5] = [2], [3] = [6], [7] = [1].
Классы эквивалентности образуют систему непустых непересекающихся
подмножеств множества
Х
, в объединении дающую все множество
Х
– т.е.
образуют разбиение множества
Х
(см. 1.1.6).
Отношение эквивалентности обозначают “
≡ “, поэтому определение
класса эквивалентности можно записать так:
}
,
{
]
[
y
x
X
y
y
x
≡
∈
=
.
1.2.6. Отношения порядка
Рассмотрим отношения
G, L
из 1.2.4, отношение
Q
из 1.2.2 и отношение
включения
V
на множестве всех подмножеств целых чисел (
B
(Z)
– булеан
множества
Z
):
∈
=
Y
X
Y
X
V
,
)
,
{(
B
(
Z
)
}
,
Y
X
⊆
.
Таблица 1.3
Свойства отношений
Отношение
Р
АР
С
АС
НС
Т
G
- + - - + +
L
+ - - + - +
Q
+ - - + - +
V
+ - - + - +

19
Мы видим, что по свойствам эти отношения разделились на два типа.
Определение. Отношение
R
на множестве
Х
, обладающее свойствами ре-
флексивности, антисимметричности, транзитивности, называется отношением
порядка на множестве
Х
(обозначается “≺”).
Определение. Отношение
R
на множестве
Х
, обладающее свойствами ан-
тирефлексивности, несимметричности, транзитивности, называется отношени-
ем строгого порядка.
Таким образом, отношения
L, Q, V
являются отношениями порядка на
соответствующих множествах, а отношение
G
– отношением строгого поряд-
ка.
1.2.7. Решение задачи 4 контрольной работы № 1
Задача. На множестве
}
5
,
4
,
3
,
2
,
1
{
=
X
задано бинарное отношение
X
X
R
×
⊆
:
)
2
(
,
,
)
,
{(
y
x
X
y
x
y
x
R
+
∈
=
делится на
}
3
. Представить отно-
шение
R
различными способами; выяснить, какими свойствами оно обладает;
является ли отношение
R
отношением эквивалентности или отношением по-
рядка.
Решение. Отношение
R
можно задать перечислением всех элементов:
{
}
)
5
,
2
(
),
2
,
5
(
),
1
,
4
(
),
4
,
1
(
),
5
,
5
(
),
4
,
4
(
),
3
,
3
(
),
2
,
2
(
),
1
,
1
(
=
R
.
Наглядно представить отношение
R
можно с помощью графика (рис. 1.10, а),
схемы (рис. 1.10, б), графа (рис. 1.11, а), матрицы отношения (рис. 1.11, б).
Выясним, какими свойствами обладает отношение.
Покажем, что отношение рефлексивно. При
y
x
=
условие “
y
x
2
+
де-
лится на 3” принимает вид
x
x
x
3
2
=
+
– делится на 3 (выполняется при лю-
бых значениях
X
x
∈ )
.

20
Проверим, является ли отношение симметричным. Пусть
y
x
2
+
делится
на 3 (т.е.
R
y
x
∈
)
,
(
). Составим пару
)
,
(
x
y
и для нее проверим характеристи-
ческое свойство отношения:
.
)
2
(
)
(
3
)
2
(
3
3
)
2
(
)
2
(
2
2
y
x
x
y
y
x
x
y
y
x
y
x
x
y
x
y
+
−
+
=
=
+
−
+
=
+
−
+
+
+
=
+
Очевидно, что
)
(
3
x
y
+
делится на 3, а
y
x
2
+
делится на 3 по условию, сле-
довательно,
x
y
2
+
делится на 3, т.е.
R
x
y
∈
)
,
(
. Отношение симметрично.
Проверим, является ли отношение транзитивным. Пусть
R
y
x
∈
)
,
(
и
R
z
y
∈
)
,
(
, т.е.
y
x
2
+
делится на 3 и
z
y
2
+
делится на 3. Будет ли делиться
на 3 выражение
z
x
2
+
, т.е. будет ли
R
z
x
∈
)
,
(
? Преобразуем
=
+ z
x
2
y
z
y
y
x
y
z
y
y
x
y
z
y
x
3
)
2
(
)
2
(
3
2
2
3
2
3
−
+
+
+
=
−
+
+
+
=
−
+
+
=
делится
на 3, т.к. первые два слагаемых делятся на 3 по условию и третье слагаемое
)
3
(
y
−
делится на 3. Значит
R
z
x
∈
)
,
(
, и отношение транзитивно. Свойства
данного отношения перечислены в таблице 1.4.
Таблица 1.4
Свойства отношения R
Отношение
Р
АР
С
АС
НС
Т
R
+ - + - - +
Отношение
R
обладает свойствами рефлексивности, симметричности,
транзитивности, следовательно, является отношением эквивалентности. На
графе отношения
R
(рис. 1.11, а) хорошо видны классы эквивалентности – это
подмножества {1,4}, {2,5}, {3} множества
Х
.